Javaを使用して貪欲なアルゴリズムを実装する方法

Java を使用して貪欲アルゴリズムを実装する方法
貪欲アルゴリズム (貪欲アルゴリズム) は、問題を解決するためのアルゴリズムのアイデアであり、現在最適なアルゴリズムを選択することを特徴としています。各ステップでの解を求め、最終的には各局所最適解を経て大域最適解に到達することを期待します。グリーディ アルゴリズムのシンプルかつ効率的な特性により、最適化問題や特定の問題を解決するときによく使用されるアルゴリズムになります。
この記事では、Java を使用して貪欲アルゴリズムを実装する方法を紹介し、具体的なコード例を示します。
1. 貪欲アルゴリズムの基本的な考え方
貪欲アルゴリズムの基本的な考え方は、他の考えられる選択肢や結果を考慮せずに、各ステップで現在の最適なソリューションを選択することです。貪欲アルゴリズムの鍵は、各ステップで最適なソリューションを決定する方法です。
2. 貪欲アルゴリズムの実装手順
貪欲アルゴリズムの実装手順は次のとおりです:
1. 問題の解空間と解セットを定義します。
2. 問題の目的関数を決定します。
3. 各ステップの選択方法を決定します。
4. 各ステップの実行戦略を決定します。
5. 終了条件に達したかどうかを判定し、達した場合は結果を出力し、そうでない場合は手順 3 に戻ります。
3. 貪欲アルゴリズムの適用可能なシナリオ
貪欲アルゴリズムは、「貪欲選択特性」を満たす問題、つまり、各ステップの最適解が現在の最適解セットに含まれている必要がある問題に適しています。 。
たとえば、変化を見つけるという問題は、貪欲なアルゴリズムを使用して解決できます。異なる額面の硬貨があると仮定すると、所定の金額の小銭を見つけるために、両替に必要な硬貨の数はできるだけ少なくなければなりません。貪欲なアルゴリズムの解決策は、毎回お釣りの際に最大額面のコインを優先することです。
4. 貪欲アルゴリズムのコード実装
以下は、貪欲アルゴリズムを使用して変更問題を解決する具体的なコード例です:
public class GreedyAlgorithm {
public static void main(String[] args) {
int[] coins = {1, 5, 10, 25, 50}; // 硬币的面额
int amount = 97; // 需要找零的金额
int[] result = greedyChange(coins, amount);
System.out.println("需要的最少硬币数量:" + result[0]);
System.out.print("找零的硬币组合:");
for (int i = 1; i < result.length; i++) {
System.out.print(result[i] + " ");
}
}
public static int[] greedyChange(int[] coins, int amount) {
int[] result = new int[coins.length + 1]; // 保存找零的结果
int count = 0; // 记录所需硬币的数量
for (int i = coins.length - 1; i >= 0; i--) {
while (amount >= coins[i]) {
amount -= coins[i]; // 从总金额中减去当前面额的硬币
result[count + 1] = coins[i];
count++;
}
}
result[0] = count; // 存储所需硬币的数量
return result;
}
}上記のコードでは、coins 配列にはコインの額面が格納され、amount は必要な小銭の額を表します。 greedyChange メソッドは貪欲アルゴリズムの特定の実装であり、result 配列を使用して変更の結果を保存し、count 変数レコードを保存します。必要なコインの数。
メイン関数では、変更する必要がある金額を 97 として定義し、greedyChange メソッドを呼び出して変更を行い、最後に必要なコインの最小数とコインを出力します。変更される組み合わせです。
上記のコード例を通じて、貪欲アルゴリズムのシンプルかつ効率的な特性がわかります。ただし、貪欲アルゴリズムはすべての問題に適した解決策ではなく、問題によっては全体的な最適解を達成できない可能性があることに注意してください。したがって、貪欲なアルゴリズムを使用して問題を解決する場合は、慎重な選択を検討する必要があります。
以上がJavaを使用して貪欲なアルゴリズムを実装する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7369
7369
 15
15
 1628
1628
 14
14
 1354
1354
 52
52
 1266
1266
 25
25
 1214
1214
 29
29
 Javaを使用して動的プログラミングアルゴリズムを実装する方法
Sep 19, 2023 am 11:16 AM
Javaを使用して動的プログラミングアルゴリズムを実装する方法
Sep 19, 2023 am 11:16 AM
Java を使用して動的プログラミング アルゴリズムを実装する方法 動的プログラミングは、多段階の意思決定問題を解決するための最適化手法です。問題を複数の段階に分解します。各段階は既知の情報に基づいて意思決定を行い、各段階での決定結果を記録します。後続の段階で使用されます。実際のアプリケーションでは、動的計画法は通常、最短経路、最大部分列合計、ナップザック問題などの最適化問題を解決するために使用されます。この記事では、Java 言語を使用して動的プログラミング アルゴリズムを実装する方法を紹介し、具体的なコード例を示します。 1. 動的計画法アルゴリズムの基本原理
 C# を使用して幅優先検索アルゴリズムを作成する方法
Sep 19, 2023 am 11:45 AM
C# を使用して幅優先検索アルゴリズムを作成する方法
Sep 19, 2023 am 11:45 AM
C# を使用して幅優先検索アルゴリズムを作成する方法 幅優先検索 (BFS) は、幅に従ってグラフまたはツリーを走査するために使用される、一般的に使用されるグラフ検索アルゴリズムです。この記事では、C# を使用して幅優先検索アルゴリズムを作成する方法を検討し、具体的なコード例を示します。アルゴリズムの原理 幅優先検索アルゴリズムの基本原理は、アルゴリズムの開始点から開始して、ターゲットが見つかるかグラフ全体が走査されるまで、検索範囲を層ごとに拡大することです。通常、キューを通じて実装されます。
 C# で貪欲アルゴリズムを実装する方法
Sep 19, 2023 am 11:48 AM
C# で貪欲アルゴリズムを実装する方法
Sep 19, 2023 am 11:48 AM
C# で貪欲アルゴリズムを実装する方法 貪欲アルゴリズム (Greedy アルゴリズム) は、一般的に使用される問題解決手法であり、毎回現在の最適解を選択して、大域的な最適解を取得することを目指します。 C# では、貪欲なアルゴリズムを使用して、多くの実際的な問題を解決できます。この記事では、C# で貪欲アルゴリズムを実装する方法を紹介し、具体的なコード例を示します。 1. 貪欲アルゴリズムの基本原理 貪欲アルゴリズムの基本的な考え方は、後続のステップの影響に関係なく、毎回現在の最適解を選択することです。このような考え方
 貪欲なアルゴリズムを使用して、PHP で最小コイン変更問題に対する効率的な解決策を実装するにはどうすればよいでしょうか?
Sep 19, 2023 am 10:22 AM
貪欲なアルゴリズムを使用して、PHP で最小コイン変更問題に対する効率的な解決策を実装するにはどうすればよいでしょうか?
Sep 19, 2023 am 10:22 AM
貪欲なアルゴリズムを使用して、PHP で最小コイン変更問題に対する効率的な解決策を実装するにはどうすればよいでしょうか?はじめに: 日常生活では、特に買い物や取引の際に小銭が必要になることがよくあります。できるだけ少ないコインを使用するには、できるだけ少ないコインを使用して釣銭金額を組み合わせる必要があります。コンピューター プログラミングでは、貪欲なアルゴリズムを使用してこの問題を解決し、効率的な解決策を得ることができます。この記事では、PHP で貪欲アルゴリズムを使用して最小コイン両替問題に対する効率的な解決策を達成する方法を紹介し、対応するコード例を示します。
 Python で PCA 主成分分析アルゴリズムを記述するにはどうすればよいですか?
Sep 20, 2023 am 10:34 AM
Python で PCA 主成分分析アルゴリズムを記述するにはどうすればよいですか?
Sep 20, 2023 am 10:34 AM
Python で PCA 主成分分析アルゴリズムを記述するにはどうすればよいですか? PCA (主成分分析) は、データの次元を削減してデータをよりよく理解して分析するために使用される、一般的に使用される教師なし学習アルゴリズムです。この記事では、Python を使用して PCA 主成分分析アルゴリズムを作成する方法を学び、具体的なコード例を示します。 PCA の手順は次のとおりです。 データを標準化します。データの各特徴の平均をゼロにし、分散を同じ範囲に調整して、
 Ford-Fulkerson アルゴリズムを解析し、Python を介して実装する
Jan 22, 2024 pm 08:09 PM
Ford-Fulkerson アルゴリズムを解析し、Python を介して実装する
Jan 22, 2024 pm 08:09 PM
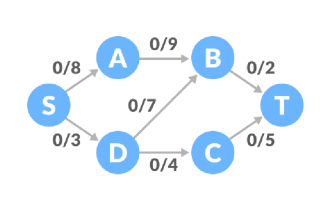
Ford-Fulkerson アルゴリズムは、ネットワーク内の最大流量を計算するために使用される貪欲なアルゴリズムです。原則として、正の残存容量を持つ増強パスを見つけることです。増強パスが見つかる限り、パスの追加とトラフィックの計算を続行できます。増加経路が存在しなくなるまで、最大流量を得ることができます。 Ford-Fulkerson アルゴリズムの残りの容量という用語は、容量からトラフィックを差し引くことを意味し、Ford-Fulkerson アルゴリズムでは、パスとして引き続き使用できるようになるまでの残りの容量は正の数になります。残余ネットワーク: 残余容量を容量として使用する、同じ頂点と辺を持つネットワークです。拡張パス: 残差グラフ内のソース ポイントから受信ポイントまでのパスであり、最終容量は 0 です。 Ford-Fulkerson アルゴリズムの原理例の考えられる概要
 Javaを使用してRSA暗号化アルゴリズムを実装する方法
Sep 20, 2023 pm 02:33 PM
Javaを使用してRSA暗号化アルゴリズムを実装する方法
Sep 20, 2023 pm 02:33 PM
Java を使用して RSA 暗号化アルゴリズムを実装する方法 RSA (Rivest-Shamir-Adleman) は非対称暗号化アルゴリズムであり、現在最も一般的に使用されている暗号化アルゴリズムの 1 つです。この記事では、Java 言語を使用して RSA 暗号化アルゴリズムを実装する方法を紹介し、具体的なコード例を示します。キー ペアの生成 まず、公開キーと秘密キーで構成される RSA キーのペアを生成する必要があります。公開キーはデータの暗号化に使用でき、秘密キーはデータの復号化に使用できます。以下は、RSA キー ペアを生成するコード例です。
 Javaで実装された推奨アルゴリズムと実装
Jun 18, 2023 pm 02:51 PM
Javaで実装された推奨アルゴリズムと実装
Jun 18, 2023 pm 02:51 PM
インターネットの発展に伴い、ネットワーク上のデータ量が爆発的に増加し、大量の情報に直面したユーザーが本当に必要なコンテンツを迅速かつ正確に見つけることが困難になっています。時代の要請に応じて登場したレコメンドアルゴリズムは、ユーザーの行動データを記録・分析することでユーザーに合わせたサービスやおすすめコンテンツを提供し、ユーザーの満足度やロイヤルティを向上させます。 Java は、大規模なソフトウェア開発に選ばれる言語として、推奨アルゴリズムの実装でもよく使われます。 1. 推奨アルゴリズム 推奨アルゴリズムは、ユーザーのインタラクション、行動、および関心データを分析およびマイニングする方法です。




