C++ で Kruskal のアルゴリズムを使用する方法

C での Kruskal アルゴリズムの使用方法
Kruskal アルゴリズムは、最小スパニング ツリー問題を解決するために一般的に使用される貪欲アルゴリズムです。 C を使用したプログラミングでは、簡単なコード例を通じて Kruskal のアルゴリズムを理解し、使用することができます。
クラスカルのアルゴリズムの基本的な考え方は、エッジの重みが最小で、すべての頂点がスパニング ツリーに含まれるまでループを形成しないエッジを継続的に選択することです。以下では、C を使用して Kruskal のアルゴリズムを実装する方法を段階的に紹介します。
ステップ 1: データの準備
まず、問題を表すグラフ データ構造を準備する必要があります。 C では、隣接行列または隣接リストを使用してグラフを表現できます。ここでは、無向グラフを表すために隣接リストを使用することを選択します。
隣接リストは、ベクトルとリンク リストの組み合わせを使用して実装できます。グラフの頂点とエッジを表す 2 つの構造を定義します。
// 图的顶点结构体
struct Vertex {
int id; // 顶点的唯一标识符
// ...
};
// 图的边结构体
struct Edge {
int start; // 边的起始顶点
int end; // 边的结束顶点
int weight; // 边的权重
// ...
};
// 定义一个无向图的类
class Graph {
public:
// 添加顶点和边的函数
void addVertex(Vertex v);
void addEdge(Edge e);
// ...
private:
// 保存顶点和边的数据结构
vector<Vertex> vertices;
list<Edge> edges;
// ...
};ステップ 2: クラスカル アルゴリズムの実装
グラフのデータ構造を準備したら、クラスカル アルゴリズムの実装を開始できます。まず、グラフのエッジを重みの小さいものから大きいものに並べ替える必要があります。次に、Union-Find を使用して、選択したエッジがサイクルを形成するかどうかを判断します。最後に、選択したエッジを最小スパニング ツリーに追加します。
以下は、Kruskal アルゴリズムの具体的な実装コードです:
// 定义并查集结构体
struct UnionFind {
vector<int> parent;
// ...
};
// 初始化并查集
void initUnionFind(UnionFind& uf, int n) {
uf.parent.resize(n);
// ...
}
// 查找根节点
int findRoot(UnionFind& uf, int x) {
if (uf.parent[x] != x) {
uf.parent[x] = findRoot(uf, uf.parent[x]);
}
return uf.parent[x];
}
// 合并两个集合
void mergeSets(UnionFind& uf, int x, int y) {
int rootX = findRoot(uf, x);
int rootY = findRoot(uf, y);
if (rootX != rootY) {
uf.parent[rootX] = rootY;
}
}
// Kruskal算法主函数
list<Edge> kruskal(Graph& graph) {
list<Edge> minSpanningTree;
// 将图的边按照权重从小到大排序
graph.edges.sort([](const Edge& e1, const Edge& e2) {
return e1.weight < e2.weight;
});
int numVertices = graph.vertices.size();
UnionFind uf;
initUnionFind(uf, numVertices);
for (const Edge& edge : graph.edges) {
int startRoot = findRoot(uf, edge.start);
int endRoot = findRoot(uf, edge.end);
// 如果两个顶点不在同一个集合中,则添加该边到最小生成树中
if (startRoot != endRoot) {
minSpanningTree.push_back(edge);
mergeSets(uf, startRoot, endRoot);
}
}
return minSpanningTree;
}ステップ 3: テスト コード
テスト関数を作成し、グラフを作成し、Kruskal アルゴリズムを呼び出して最小スパニング ツリーを出力します。 :
void testKruskal() {
Graph graph;
// 添加顶点和边
// ...
list<Edge> minSpanningTree = kruskal(graph);
// 输出最小生成树
for (const Edge& edge : minSpanningTree) {
cout << edge.start << " -> " << edge.end << ", weight: " << edge.weight << endl;
}
}
int main() {
testKruskal();
return 0;
}上記は、C を使用して Kruskal のアルゴリズムを実装する簡単な例です。この例を通じて、クラスカルのアルゴリズムをよりよく理解し、使用して最小スパニング ツリー問題を解決することができます。
以上がC++ で Kruskal のアルゴリズムを使用する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7465
7465
 15
15
 1376
1376
 52
52
 77
77
 11
11
 18
18
 19
19
 C++ で Kruskal のアルゴリズムを使用する方法
Sep 19, 2023 pm 04:10 PM
C++ で Kruskal のアルゴリズムを使用する方法
Sep 19, 2023 pm 04:10 PM
C++ でのクラスカルのアルゴリズムの使用方法 クラスカルのアルゴリズムは、最小スパニング ツリー問題を解決するために一般的に使用される貪欲アルゴリズムです。 C++ でのプログラミングでは、簡単なコード例を通じてクラスカルのアルゴリズムを理解し、使用することができます。クラスカルのアルゴリズムの基本的な考え方は、エッジの重みが最小で、すべての頂点がスパニング ツリーに含まれるまでループを形成しないエッジを継続的に選択することです。以下では、C++ を使用して Kruskal のアルゴリズムを実装する方法を段階的に紹介します。ステップ 1: データの準備 まず最初に、
 C++ を使用して組み込みシステムのスケジュールされたタスク機能を実装する方法
Aug 27, 2023 pm 12:05 PM
C++ を使用して組み込みシステムのスケジュールされたタスク機能を実装する方法
Aug 27, 2023 pm 12:05 PM
C++ を使用して組み込みシステムのスケジュールされたタスク関数を実装する方法 組み込みシステムでは、多くの場合、スケジュールされたタスク関数、つまり特定の時間間隔内にいくつかのタスクを実行する必要があります。 C++ は強力なプログラミング言語として、そのような機能を実現するための多くのツールとライブラリを提供します。この記事では、C++ プログラミング言語を使用して組み込みシステムにスケジュールされたタスク関数を実装する方法を紹介し、いくつかのコード例を示します。タイマー割り込みの使用 組み込みシステムでは、タイマー割り込みを使用して、スケジュールされたタスク機能を実装できます。タイマーをセットすることで
 Prim と Kruskal の最小スパニング ツリー アルゴリズムが有向グラフで失敗するのはなぜですか?
Sep 02, 2023 pm 05:29 PM
Prim と Kruskal の最小スパニング ツリー アルゴリズムが有向グラフで失敗するのはなぜですか?
Sep 02, 2023 pm 05:29 PM
プリムの方法とクラスカルのアルゴリズムは、無向グラフで MST (最小スパニング ツリー) を見つけるための 2 つの一般的な方法です。ただし、これらの手法では、有向グラフの正しい MST を生成できません。これは、有向グラフがプリムとクラスカルのアルゴリズムで使用される基本的な仮定と手法に適合しないためです。プリムのアルゴリズム まず、プリムのアルゴリズムがあります。これは、すべての頂点がカバーされるまで貪欲に拡張する最小スパニング ツリーにエッジを追加することを含みます。 MST 内の頂点は、最小の重みを持つエッジを介して MST の外側の頂点に接続されます。無向グラフ内のすべてのエッジは任意の方向に移動できるため、MST から外部頂点までの最短パスを見つけるのは簡単です。ただし、有向グラフではエッジは常に一方向を向いており、直線が存在しない場合があります。
 高速検索アルゴリズムとそのPHPへの応用
Jun 22, 2023 pm 05:31 PM
高速検索アルゴリズムとそのPHPへの応用
Jun 22, 2023 pm 05:31 PM
PHP は、人気のあるサーバーサイド プログラミング言語として、Web アプリケーション開発において不可欠な役割を果たしています。実際の開発では、大量のデータに対して検索や検索などの操作を行うことが多く、その際、検索アルゴリズムの高速化は非常に重要な方向性となっています。この記事では、PHPでよく使われる高速検索アルゴリズムとその応用例を紹介します。 1. 概要 データ構造において、検索とはデータ集合の中から指定した条件でデータを検索することをいい、一般的な検索方法には線形検索、二分検索、ハッシュ検索などが挙げられます。線形探索
 C++ で自動運転とインテリジェント交通システムを実装するにはどうすればよいですか?
Aug 26, 2023 am 08:58 AM
C++ で自動運転とインテリジェント交通システムを実装するにはどうすればよいですか?
Aug 26, 2023 am 08:58 AM
C++ で自動運転とインテリジェント交通システムを実装するにはどうすればよいですか?自動運転と知能型交通システムは現在、人工知能の分野で注目を集めており、その応用分野は交通、安全保護、都市計画など多くの側面に広がっています。この記事では、C++ プログラミング言語を使用して自動運転およびインテリジェント交通システムを実装する方法を検討し、関連するコード例を示します。自動運転と高度道路交通システムの基本原理を理解する 自動運転システムとは、コンピューター、センサー、その他の機器を使用して車両を自律的に移動および運転する技術を指します。リアルタイムで認識する必要がある
 C++ を使用してリアルタイム機能を備えた組み込みシステムを実装する方法
Aug 25, 2023 pm 03:18 PM
C++ を使用してリアルタイム機能を備えた組み込みシステムを実装する方法
Aug 25, 2023 pm 03:18 PM
C++ を使用してリアルタイム機能を備えた組み込みシステムを実装する方法 はじめに: 技術の継続的な発展に伴い、組み込みシステムはさまざまな分野で広く使用されています。リアルタイム機能は、組み込みシステム、特に外部イベントへの即時応答が必要なシナリオにおいて重要な機能です。この記事では、C++ 言語を使用してリアルタイム機能を備えた組み込みシステムを実装する方法とコード例を紹介します。リアルタイム オペレーティング システム (RTOS) リアルタイム オペレーティング システム (RTOS) は、リアルタイム機能を実現するための鍵です。 RTOSにはタスクスケジューリング機能があり、
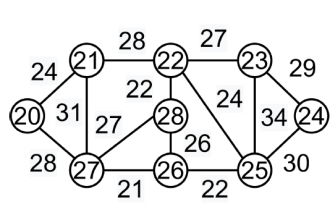 Kruskal の最小スパニング ツリー アルゴリズム - C++ の貪欲なアルゴリズム
Aug 28, 2023 pm 03:05 PM
Kruskal の最小スパニング ツリー アルゴリズム - C++ の貪欲なアルゴリズム
Aug 28, 2023 pm 03:05 PM
スパニング ツリーは、すべての頂点を接続する有向無向グラフのサブグラフです。グラフ内には多数のスパニング ツリーが存在する場合があります。各グラフの最小スパニング ツリー (MST) の重みは、他のすべてのスパニング ツリーと同じかそれより小さくなります。重みはスパニング ツリーのエッジに割り当てられ、合計が各エッジに割り当てられた重みになります。 V はグラフ内の頂点の数であるため、V をエッジの数とすると、最小スパニング ツリーのエッジの数は (V-1) になります。クラスカルのアルゴリズムを使用して最小スパニング ツリーを見つけます。すべてのエッジは重みの降順以外に配置する必要があります。最小の辺を選択します。ループが形成されていない場合は、エッジが含まれます。ステップ 2 は、スパニング ツリーに (V-1) 個のエッジができるまで実行する必要があります。この場合、貪欲なアプローチを使用するように言われます。欲張りなオプションは、最小の重みを持つエッジを選択することです。例: このグラフの最小スパニング ツリーは (9-1)=8 です。
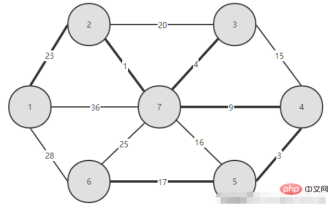 Java で Kruskal アルゴリズムを実装する方法
May 11, 2023 pm 10:19 PM
Java で Kruskal アルゴリズムを実装する方法
May 11, 2023 pm 10:19 PM
最小スパニング ツリーを構築するための別のアルゴリズム、つまりクラスカル アルゴリズムを導入します: グラフ G = (V, E) を無向接続加重グラフ V = {1, 2,...n} とし、最小スパニング ツリーをT = (V, TE)、ツリーの初期状態は、n 個のノードのみとエッジを持たない非接続グラフです T = (V, {})。クラスカルのアルゴリズムは、これらの n ノードを n 個の孤立した接続された枝として扱います。まず、すべてのエッジを重みに従って小さいものから大きいものまで並べ替えます。次に、T で選択されるエッジの数が n-1 未満の場合は、次のような貪欲な選択を行います。 エッジ (i, j) を選択します。エッジ セット E 内の最小の重みを持つエッジ (i, j) をセット TE に追加してもサイクルが生成されない場合は、エッジ (i, j) をエッジ セット TE に追加します。つまり、エッジ (i 、j) 2 つのブランチを 1 つにマージします。




