Floyd-Warshal アルゴリズムを使用して、任意の 2 つのノード間の最短パスを検索します。
C コードまたは期待値として定義されるマクロがあり、ユーザーが必要とするたびに再利用されます。フロイド・ウォルシャル アルゴリズムは、指定された重み付きグラフ内の頂点のすべてのペア間の最短経路を見つけるプロセスです。このアルゴリズムは動的プログラミング アプローチに従って、最小重みグラフを見つけます。
フロイト・ワルシャルアルゴリズムの意味を図で理解しましょう -
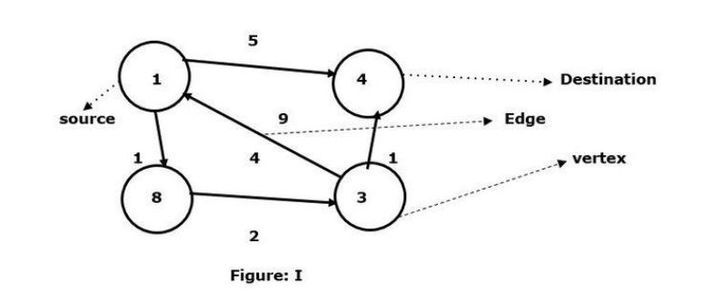
頂点 1 をソース、頂点 4 を目的地として、それらの間の最短パスを見つけます。
ターゲット頂点 4 に接続できるパスが 2 つあることがわかりました。
1 -> 4 – エッジの重みは 5
1 -> 8 -> 3 -> 4 – エッジの重み (1 2 1) は 4 です。
与えられたグラフ I では、2 つの頂点を接続する最小のエッジが表示されます。ここで、頂点 8 と頂点 3 の間のパスは、頂点 1 と頂点 4 を接続し、エッジは 4## になります。 #。一方、頂点 1 と頂点 4 の間には有向辺があり、辺の重みは 5 です。
次に、2 つの重み、つまり4 と 5 を比較します。したがって、ここでの 4 は、Floyd Warshall アルゴリズムに従って計算されたグラフの最小重みです。
この記事では、Floyd Warshall アルゴリズムを使用して、任意の 2 つのノード間の最短パスを見つけます。###文法###
プログラムでは次の構文が使用されます -リーリー
パラメータ
data_type[][]
- ユーザーが指定したデータ型。最初の配列は行を表し、2 番目の配列は列を表します。したがって、これは 2 次元配列を表します。array_name
- 配列に付けられた名前。###アルゴリズム###
ヘッダー ファイル'iostream'
でプログラムを開始し、マクロの位置を- 'INF'
- (無限大) として定義します。これは、後で 2 つの条件を満たすためです。次元配列行列と if-else ステートメント。
次に、'printPath'
という名前のグローバル関数定義を作成し、3 つのパラメーター、つまり 'parent[]'、'i' - 、および
を受け入れます。 j' パスが存在することを確認します。 次に、main 関数を開始し、頂点の数を表す値 ‘4’
を変数 ‘V’ - に保存します。次に、値を隣接行列の形式で変数
'dist[V][V]' に保存します。ご存知のとおり、dist[i][j] は 2D 行列を表し、'i' から 'j' までのエッジの重みを定義します。隣接行列を保存します。 次に、変数 'parent'
の 2D 配列を初期化しています。サイズは [V][V] - です。
この変数では、頂点の各ペア 'i' と
'j' w.r.t -
If (dist[i][j] != INF && i != j) { parent[i][j] = i;}
の中国語訳は次のとおりです:parent[i][j] = i;} - 'and' (&&)
演算子を使用して 2 つの条件を表現します。両方の条件が満たされた場合、'i' は 'parent[i ][j] に格納されます。 ]' を実行し、パスが存在することを確認します。
#########他の{ parent[i][j] = -1;} の中国語訳は次のとおりです:parent[i][j] = -1;}else ステートメントでは、パスが存在しないことを確認するために、「-1」を "parent[i][j]"
に初期化します。 -
次に、3 つのネストされたfor ループから開始し、0 ~ V-1 の範囲にある k 個の頂点を適用します。この範囲を利用して、最短距離とパスが更新されます。 3 番目のネストされたループでは、
のような次の条件を使用します。
リーリー
- ここで、K は 2 次元配列行列の行部分と列部分を更新し、新しく更新された最短経路と距離を検証します。
次に、次の条件を与えて、すべての頂点ペアの最短距離とパスを出力します。
'parent[i][j]' を表示するために使用します。 ネストされた 2 つの for ループを使用して、最短パスを見つけます。最初の for ループは、行列内の行を反復処理します。次に、2 番目の for ループを通じて行列内の列を反復処理し、if-else ステートメント -
を使用して次の条件を確認します。- if ステートメントでは、
- 2 番目の for ループの下で if ステートメントを使用して、dist[i][j] が無限大に等しいかどうかを確認します。無限大であることが判明した場合は「INF」を出力し、それ以外の場合は最短パスを出力します。
- 最後に、3 つのパラメータ (parent[i]、i、j) を渡して、
- 'printPath()'
という名前の関数を呼び出します。
-
#include <iostream> using namespace std; #define INF 1000000000 // Infinity void printPath(int parent[], int i, int j) { if (i == j) cout << i << " "; else if (parent[j] == -1) cout << "No path exists"; else { printPath(parent, i, parent[j]); cout << j << " "; } } int main() { int V = 4; // V represent number of vertices int dist[V][V] = {{0, 2, INF, 4}, {6, 0, 5, 3}, {INF, 10, 0, 1}, {7, 9, 8, 0}}; // Represent the graph using adjacency matrix // Apply the Floyd Warshall algorithm to find the shortest paths int parent[V][V]; for (int i = 0; i < V; i++) { for (int j = 0; j < V; j++) { if (dist[i][j] != INF && i != j) parent[i][j] = i; else parent[i][j] = -1; } } // update the path and distance using the k vertex range from 0 to V-1. for (int k = 0; k < V; k++) { for (int i = 0; i < V; i++) { for (int j = 0; j < V; j++) { if (dist[i][j] > dist[i][k] + dist[k][j]) { dist[i][j] = dist[i][k] + dist[k][j]; parent[i][j] = parent[k][j]; } } } } // Print shortest distances and paths between all pairs of vertices for (int i = 0; i < V; i++) { for (int j = 0; j < V; j++) { cout << "The Shortest distance between " << i << " and " << j << " is "; if (dist[i][j] == INF) cout << "INF "; else cout << dist[i][j] << " "; cout << "and the shortest path is:- "; printPath(parent[i], i, j); cout << endl; } } return 0; }ログイン後にコピー输出
The Shortest distance between 0 and 0 is 0 and the shortest path is:- 0 The Shortest distance between 0 and 1 is 2 and the shortest path is:- 0 1 The Shortest distance between 0 and 2 is 7 and the shortest path is:- 0 1 2 The Shortest distance between 0 and 3 is 4 and the shortest path is:- 0 3 The Shortest distance between 1 and 0 is 6 and the shortest path is:- 1 0 The Shortest distance between 1 and 1 is 0 and the shortest path is:- 1 The Shortest distance between 1 and 2 is 5 and the shortest path is:- 1 2 The Shortest distance between 1 and 3 is 3 and the shortest path is:- 1 3 The Shortest distance between 2 and 0 is 8 and the shortest path is:- 2 3 0 The Shortest distance between 2 and 1 is 10 and the shortest path is:- 2 1 The Shortest distance between 2 and 2 is 0 and the shortest path is:- 2 The Shortest distance between 2 and 3 is 1 and the shortest path is:- 2 3 The Shortest distance between 3 and 0 is 7 and the shortest path is:- 3 0 The Shortest distance between 3 and 1 is 9 and the shortest path is:- 3 1 The Shortest distance between 3 and 2 is 8 and the shortest path is:- 3 2 The Shortest distance between 3 and 3 is 0 and the shortest path is:- 3
ログイン後にコピー结论
我们学习了使用Floyd Warshall算法找到任意两个节点之间的最短路径的概念。我们使用邻接矩阵作为程序的输入,通过它我们找到了最短路径和距离。此外,为了更新路径和距离,我们使用了k个顶点来更新行和列。在我们的日常生活中,我们在谷歌地图上搜索最短路线或路径,从一个起点到目的地。
ネストされた 2 つの for ループを使用して、最短距離とパスを出力します。
以上がFloyd-Warshal アルゴリズムを使用して、任意の 2 つのノード間の最短パスを検索します。の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7450
7450
 15
15
 1374
1374
 52
52
 77
77
 11
11
 14
14
 7
7
 ツリー内の最短パスのすべてのペアの合計
Aug 28, 2023 pm 03:17 PM
ツリー内の最短パスのすべてのペアの合計
Aug 28, 2023 pm 03:17 PM
ツリーでは、「ノードのすべてのペアの最短パスの合計」という用語は、ノードのすべてのペアの個々の最短パスの合計の計算を指します。効果的な方法は、デュアル DFS (深さ優先検索) アルゴリズムを使用することです。選択したノードと他のすべてのノードの間の距離は、最初の DFS パス中に決定されます。ツリーは 2 回目の DFS パス中に再び走査され、各ノードを潜在的な LCA (最下位共通祖先) とみなして、選択された LCA の子孫ノードのペア間の距離の合計を計算します。この方法を使用すると、ツリー内のノードのすべてのペアの最短パスの合計を計算し、理想的な解を確実に得ることができます。 使用される方法 デュアル DFS (深さ優先検索) メソッド ダイナミック プログラミング メソッド ツリーのデュアル DFS (深さ優先検索) メソッド すべて最短経路のペア
 ノード X から始まるサブツリーの最小重みと最大 D の距離を照会します。
Aug 25, 2023 am 11:25 AM
ノード X から始まるサブツリーの最小重みと最大 D の距離を照会します。
Aug 25, 2023 am 11:25 AM
コンピューター プログラミングを行う場合、特定のノードから D 単位以上離れたノードをサブツリーに含めることができないという条件で、特定のノードに由来するサブツリーの最小重みを見つけることが必要になる場合があります。この問題は、グラフ理論、ツリーベースのアルゴリズム、ネットワーク最適化など、さまざまな分野やアプリケーションで発生します。サブツリーは、指定されたノードがサブツリーのルート ノードとして機能する、より大きなツリー構造のサブセットです。サブツリーには、ルート ノードのすべての子孫とそれらの接続エッジが含まれます。ノードの重みは、そのノードに割り当てられた特定の値を指し、その重要性、重要性、またはその他の関連するメトリックを表すことができます。この問題の目標は、ルート ノードから最大 D 単位離れたノードにサブツリーを制限しながら、サブツリー内のすべてのノード間の最小重みを見つけることです。次の記事では、サブツリーから最小重みをマイニングする複雑さについて詳しく説明します。
 Javaを使用して最短パスアルゴリズムを実装する方法
Sep 19, 2023 am 08:18 AM
Javaを使用して最短パスアルゴリズムを実装する方法
Sep 19, 2023 am 08:18 AM
Java を使用して最短パス アルゴリズムを実装する方法の概要: 最短パス アルゴリズムはグラフ理論の重要なアプリケーションであり、ネットワーク ルーティング、マップ ナビゲーション、その他の分野で広く使用されています。この記事では、Java を使用して最短パス アルゴリズムを実装する方法を学び、具体的なコード例を示します。アルゴリズムのアイデア: 最短経路アルゴリズムを実装するには多くの方法がありますが、その中で最も有名な 2 つのアルゴリズムは、ダイクストラ アルゴリズムと A* アルゴリズムです。ここでは、ダイクストラのアルゴリズムの実装に焦点を当てます。ダイクストラのアルゴリズムの基礎
 Vue と jsmind を使用してマインド マップのノード コピーおよびカット機能を実装するにはどうすればよいですか?
Aug 15, 2023 pm 05:57 PM
Vue と jsmind を使用してマインド マップのノード コピーおよびカット機能を実装するにはどうすればよいですか?
Aug 15, 2023 pm 05:57 PM
Vue と jsmind を使用してマインド マップのノード コピーおよびカット機能を実装するにはどうすればよいですか?マインド マップは、考えを整理し、思考ロジックを整理するのに役立つ一般的な思考ツールです。ノードのコピーとカット機能は、マインド マップでよく使用される操作であり、既存のノードをより便利に再利用し、思考整理の効率を向上させることができます。この記事では、Vue と jsmind の 2 つのツールを使用して、マインド マップのノードのコピーとカット機能を実装します。まず、Vue と jsmind をインストールし、
 jsでノードを削除する方法は何ですか
Sep 01, 2023 pm 05:00 PM
jsでノードを削除する方法は何ですか
Sep 01, 2023 pm 05:00 PM
js でノードを削除するメソッドは次のとおりです: 1. RemoveChild() メソッドは、指定された子ノードを親ノードから削除するために使用されます。これには 2 つのパラメータが必要です。最初のパラメータは削除される子ノードで、2 番目のパラメータは次のとおりです。親ノード ノード; 2.parentNode.removeChild() メソッドは、親ノードを介して直接呼び出して子ノードを削除できます; 3.remove() メソッドは、親ノードを指定せずにノードを直接削除できます; 4. innerHTML 属性は、ノードのコンテンツを削除するために使用されます。
 Floyd-Warshal アルゴリズムを使用して、任意の 2 つのノード間の最短パスを検索します。
Sep 20, 2023 pm 02:21 PM
Floyd-Warshal アルゴリズムを使用して、任意の 2 つのノード間の最短パスを検索します。
Sep 20, 2023 pm 02:21 PM
C++ にはコードの一部または期待値として定義されるマクロがあり、ユーザーが必要とするたびに再利用されます。フロイド・ウォルシャル アルゴリズムは、指定された重み付きグラフ内の頂点のすべてのペア間の最短経路を見つけるプロセスです。このアルゴリズムは動的プログラミング アプローチに従って、最小重みグラフを見つけます。図を通してフロイド・ウォルシャルアルゴリズムの意味を理解しましょう - 頂点 1 をソースとして、頂点 4 を目的地として取り、それらの間の最短パスを見つけます。ターゲット頂点 4 に接続できるパスが 2 つあることがわかりました。 1->4 – エッジの重みは 51->8->3->4 – エッジの重み (1+2+1)は4です。与えられたグラフ I では、2 つの頂点を接続する最小のエッジが表示されます。ここに頂点があります
 js で要素ノードを作成、削除、追加、置換する方法 (コード例付き)
Aug 06, 2022 pm 05:26 PM
js で要素ノードを作成、削除、追加、置換する方法 (コード例付き)
Aug 06, 2022 pm 05:26 PM
この記事では主にjsで要素ノードを作成、削除、追加、置換する方法を紹介しますので、困っている方の参考になれば幸いです。
 PHP アルゴリズム設計のアイデア: グラフの最短経路問題に対する効率的な解決策を達成するには?
Sep 19, 2023 pm 03:43 PM
PHP アルゴリズム設計のアイデア: グラフの最短経路問題に対する効率的な解決策を達成するには?
Sep 19, 2023 pm 03:43 PM
PHP アルゴリズム設計のアイデア: グラフの最短経路問題に対する効率的な解決策を達成するには?実際の開発では、地図ナビゲーション、ネットワークルーティング、物流流通などの分野で、最短経路の問題を解決する必要があることがよくあります。この種の問題を解決するには、グラフの最短パス アルゴリズムが鍵となります。グラフは、頂点のセットとエッジのセットで構成されます。頂点はノードを表し、エッジはノード間の関係を表します。最短パスの問題は、2 つのノードを接続する最短パスを見つけることです。 PHP では、さまざまなアルゴリズムを使用して最短経路問題を解決できます。その中で最も有名なものは次のとおりです。




