C++ でナップザック問題アルゴリズムを使用する方法

C でナップサック問題アルゴリズムを使用する方法
ナップサック問題は、コンピューター アルゴリズムにおける古典的な問題の 1 つです。アイテムのトータル価値を最大限に高めるバックパック。この記事では、C で動的計画アルゴリズムを使用してナップザック問題を解決する方法と、具体的なコード例を詳しく紹介します。
まず、ナップザック問題の入力と出力を定義する必要があります。入力には、アイテムの重み配列 wt[]、アイテムの値配列 val[]、およびバックパックの容量 W が含まれます。アウトプットは、価値を最大化するためにバックパックに入れるアイテムを選択することです。定義は次のとおりです。
int knapSack(int W, int wt[], int val[], int n) {
// 动态规划表格
int dp[n+1][W+1];
// 填充动态规划表格
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= W; j++) {
if (i == 0 || j == 0)
dp[i][j] = 0; // 边界条件
else if (wt[i - 1] <= j)
dp[i][j] = max(val[i - 1] + dp[i - 1][j - wt[i - 1]], dp[i - 1][j]);
else
dp[i][j] = dp[i - 1][j];
}
}
return dp[n][W]; // 返回最大价值
}上記のコードでは、2 次元配列 dp[][] を使用して動的プログラミングの状態遷移テーブルを表します。ここで、dpi は最初の i 項目の選択を表します。 、バックパックの容量は j ケースの最大合計値です。特定のアルゴリズムは次のように実装されます。
- 2 次元配列 dp[][] の最初の行と列を 0 に初期化します。これは、選択する項目がないこと、または最大値が存在しないことを意味します。容量が 0 の場合の合計値は 0;
行 1 列 1 から開始して、各 dpi を計算します:
- 現在のアイテムの重量 wt[i -1] はバックパックの容量 j 以下で、アイテムを入れるか入れないかを選択でき、両方の場合で最大の合計値を選択できます。
- 現在のアイテムの重量が wt[i -1] はバックパックの容量 j より大きく、現在のアイテムを入れることはできません、合計値は前の状態、つまり dpi-1 に等しいです;
- 最終的に戻りますdpn は、最初の n 個のアイテムが選択されており、バックパックの容量が最大合計値 W であることを示します。
以下は、ナップザック問題アルゴリズムを使用したサンプル コードです。
#includeusing namespace std; int knapSack(int W, int wt[], int val[], int n) { // 动态规划表格 int dp[n+1][W+1]; // 填充动态规划表格 for (int i = 0; i <= n; i++) { for (int j = 0; j <= W; j++) { if (i == 0 || j == 0) dp[i][j] = 0; // 边界条件 else if (wt[i - 1] <= j) dp[i][j] = max(val[i - 1] + dp[i - 1][j - wt[i - 1]], dp[i - 1][j]); else dp[i][j] = dp[i - 1][j]; } } return dp[n][W]; // 返回最大价值 } int main() { int val[] = {60, 100, 120}; int wt[] = {10, 20, 30}; int W = 50; int n = sizeof(val) / sizeof(val[0]); cout << "最大总价值为:" << knapSack(W, wt, val, n) << endl; return 0; }
上記のコードを実行すると、出力結果の最大合計値は 220 になります。これは、ナップザック問題のアルゴリズムを使用した場合に、容量は50、アイテム1とアイテム3を選択することで獲得できる合計値の最大値となります。
上記の動的プログラミング手法に加えて、バックトラッキング アルゴリズムや貪欲アルゴリズムなどの他の手法を使用してナップザック問題を解決することもできます。上記は、C でナップザック問題アルゴリズムを使用する方法について詳しく説明したものです。お役に立てば幸いです。
以上がC++ でナップザック問題アルゴリズムを使用する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7517
7517
 15
15
 1378
1378
 52
52
 79
79
 11
11
 21
21
 66
66
 C# を使用して動的プログラミング アルゴリズムを作成する方法
Sep 20, 2023 pm 04:03 PM
C# を使用して動的プログラミング アルゴリズムを作成する方法
Sep 20, 2023 pm 04:03 PM
C# を使用して動的プログラミング アルゴリズムを作成する方法 概要: 動的プログラミングは、最適化問題を解決するための一般的なアルゴリズムであり、さまざまなシナリオに適しています。この記事では、C# を使用して動的プログラミング アルゴリズムを作成する方法を紹介し、具体的なコード例を示します。 1. 動的プログラミング アルゴリズムとは何ですか? 動的プログラミング (DP) は、重複する部分問題と最適な部分構造特性を持つ問題を解決するために使用されるアルゴリズムのアイデアです。動的プログラミングでは、問題を解決するためのいくつかのサブ問題に分解し、各サブ問題の解決策を記録します。
 PHP アルゴリズム分析: 動的プログラミング アルゴリズムを使用して最長回文部分文字列問題を解決するにはどうすればよいですか?
Sep 19, 2023 pm 12:19 PM
PHP アルゴリズム分析: 動的プログラミング アルゴリズムを使用して最長回文部分文字列問題を解決するにはどうすればよいですか?
Sep 19, 2023 pm 12:19 PM
PHP アルゴリズム分析: 動的プログラミング アルゴリズムを使用して最長回文部分文字列問題を解決するにはどうすればよいですか?動的計画法 (動的計画法) は、多くの複雑な問題を解決できる、一般的に使用されるアルゴリズムのアイデアです。そのうちの 1 つは、最長回文部分文字列の問題です。これは、文字列内の最長回文部分文字列の長さを見つけることです。この記事では、PHP を使用してこの問題を解決する動的プログラミング アルゴリズムを作成する方法を紹介し、具体的なコード例を示します。まず、最長の回文部分文字列を定義しましょう。回文文字列とは、前から見ても後ろから読んでも同じ文字列を指します。
 C# を使用してナップザック問題アルゴリズムを作成する方法
Sep 19, 2023 am 09:21 AM
C# を使用してナップザック問題アルゴリズムを作成する方法
Sep 19, 2023 am 09:21 AM
C# を使用してナップザック問題アルゴリズムを作成する方法 ナップザック問題 (ナップザック問題) は、古典的な組み合わせ最適化問題であり、指定された容量と一連の項目を備えたナップザックを記述します。各項目は独自の値と重みを持ちます。目標は、バックパックの容量を超えずに、バックパックに詰めたアイテムの合計価値を最大化する最適な戦略を見つけることです。 C# では、動的プログラミングによってナップザック問題を解決できます。具体的な実装は次のとおりです。 usingSystem;namespace
 C++ でナップザック問題アルゴリズムを使用する方法
Sep 21, 2023 pm 02:18 PM
C++ でナップザック問題アルゴリズムを使用する方法
Sep 21, 2023 pm 02:18 PM
C++ でのナップザック問題アルゴリズムの使用方法 ナップザック問題は、コンピュータ アルゴリズムにおける古典的な問題の 1 つであり、アイテムの合計価値を最大化するために、指定されたナップザック容量の下でナップザックに入れるいくつかのアイテムを選択する方法が含まれます。この記事では、C++ の動的プログラミング アルゴリズムを使用してナップザック問題を解決する方法と、具体的なコード例を詳しく紹介します。まず、ナップサック問題の入力と出力を定義する必要があります。入力には、アイテムの重み配列 wt[]、アイテムの値配列 val[]、およびバックパックの容量 W が含まれます。出力はどのオブジェクトが選択されているかです。
 動的計画法アルゴリズムを使用してPHPのナップザック問題を解決し、最適な解決策を得るにはどうすればよいですか?
Sep 21, 2023 am 10:33 AM
動的計画法アルゴリズムを使用してPHPのナップザック問題を解決し、最適な解決策を得るにはどうすればよいですか?
Sep 21, 2023 am 10:33 AM
動的計画法アルゴリズムを使用してPHPのナップザック問題を解決し、最適な解決策を得るにはどうすればよいですか?ナップザック問題は、コンピューター サイエンスにおける古典的な組み合わせ最適化問題の 1 つです。アイテムのセットとナップザックの容量が与えられた場合、ナップザック内のアイテムの合計価値を最大化するためにナップザックに入れるアイテムをどのように選択するかが、解決すべきナップザック問題の核心です。動的プログラミングは、ナップザック問題を解決する一般的な方法の 1 つです。問題をサブ問題に分割し、そのサブ問題に対する解決策を保存することにより、最終的に最適な解決策が得られます。以下では、PHP で動的計画アルゴリズムを使用する方法を詳しく説明します。
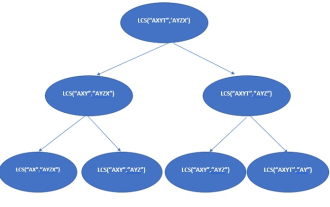 Java でのメモ化 (1D、2D、および 3D) 動的プログラミング
Aug 23, 2023 pm 02:13 PM
Java でのメモ化 (1D、2D、および 3D) 動的プログラミング
Aug 23, 2023 pm 02:13 PM
メモ化は、提供された入力の結果 (配列に格納) を記録することで、同じ入力セットに対してメソッドが複数回実行されないようにし、再帰的アルゴリズムのパフォーマンスを向上させるために使用される動的プログラミングに基づく手法です。メモ化は、再帰的メソッドを実装するトップダウンのアプローチを通じて実現できます。基本的なフィボナッチ数列の例を通してこの状況を理解しましょう。 1-D メモ化 非定数パラメーターが 1 つだけ (値が変化するパラメーターは 1 つだけ) の再帰的アルゴリズムを検討します。そのため、この方法は 1-D メモ化と呼ばれます。次のコードは、フィボナッチ数列の N 番目 (N までのすべての項) を見つけるためのものです。例 publicintfibonacci(intn){ &nb
 PHPの動的計画法アルゴリズムを詳しく解説
Jul 07, 2023 am 10:48 AM
PHPの動的計画法アルゴリズムを詳しく解説
Jul 07, 2023 am 10:48 AM
PHP における動的計画法アルゴリズムの詳細な説明 動的計画法 (Dynamic Programming) は、問題を解決するためのアルゴリズムの考え方であり、問題をより小さな部分問題に分解し、解決された部分問題の結果を使用することで全体的な問題を解決します。 PHP では、動的プログラミング アルゴリズムは、最短パス、文字列マッチング、ナップサック問題など、コンピューター サイエンスや数学の多くの分野で広く使用できます。この記事では、PHP の動的プログラミング アルゴリズムの原理を詳しく紹介し、コード例を示して説明します。 1. 動的計画計算
 PHP を使用してナップザック問題アルゴリズムを実装する方法
Jul 09, 2023 am 09:15 AM
PHP を使用してナップザック問題アルゴリズムを実装する方法
Jul 09, 2023 am 09:15 AM
PHP を使用してナップザック問題アルゴリズムを実装する方法。ナップザック問題は古典的な組み合わせ最適化問題です。その目標は、限られたバックパック容量の下で合計値を最大化するアイテムのセットを選択することです。この記事では、PHP を使用してナップザック問題のアルゴリズムを実装する方法と、対応するコード例を紹介します。ナップザック問題の説明 ナップザック問題は次のように説明できます。容量 C と N 個のアイテムを持つナップザックが与えられたとします。各項目 i には重み wi と値 vi があります。これらの N 個の項目から、次のような項目をいくつか選択する必要があります。




