チューリングの原理を再考し、矛盾による証明の力を感じてください。
アルゴリズムは至る所に普及しており、正確な数学用語で表現できるすべての問題には、対応するアルゴリズムがあるようです。しかし、そうではありません。実際には、一見単純に見える問題の中には、アルゴリズムでは決して解決できないものもあります。コンピュータ科学者の先駆者であるアラン チューリングは、これをほぼ 1 世紀前の論文で証明しました。この問題を解決するために、彼は現代のコンピューターサイエンスを開始する計算数学モデルを提案しました。
チューリングは、直観に反する戦略を使用して、この画期的な結果を実証しました。彼は、それを解決しようとするすべての試みに抵抗する問題を定義しました。 「例えば、私があなたに何をしているのかと尋ねたら、あなたの答えが何であれ、私は『私がやろうとしていることはあなたが言ったこととは違う』と言うだろう」とマサチューセッツ工科大学(MIT)の大学院生ラーフル・イランゴ氏は語った。理論的なコンピューターサイエンス。 書き直された内容: チューリングは、直観に反する戦略でこの画期的な結果を実証しました。彼は、それを解決しようとするすべての試みに抵抗する問題を定義しました。 「たとえば、私があなたに何をしているのかと尋ねたら、あなたの答えが何であれ、私は『私がやろうとしていることはあなたが言ったこととは違う』と言うだろう」とマサチューセッツ工科大学(MIT)の大学院生ラーフル・イランゴ氏は語った。理論的コンピューターサイエンス
#チューリングの戦略は、「対角証明」と呼ばれる長年の数学的手法に基づいています。以下は、彼の証明の背後にあるロジックの簡単な説明です。文字列
対角線の証明は、文字列に関する問題を解決するための巧妙なトリックから来ています。ビットは 0 または 1 です。問題の説明は次のとおりです。文字列のリストが与えられ、リスト内のすべての文字列が同じ長さである場合、リストにない新しい文字列をどのように生成できますか?
書き直された内容: 最も簡単な戦略の 1 つは、考えられるすべての文字列を順番に検討することです。 5 つの文字列があり、それぞれに 5 ビットがあるとします。まず、リストに 00000 が存在するかどうかを繰り返し確認します。存在しない場合は問題は解決されており、存在する場合は 00001 に進み、プロセスを繰り返します。この方法はシンプルですが、長い文字列から生じる長いリストの場合は遅くなります。 Diagonal は、存在しない文字列を段階的に構築するための実行可能な代替手段であることがわかります。リストの最初の文字列の最初のビットから始めて、それを反転すると、これが新しい文字列の最初のビットになります。次に、2 番目の文字列の 2 番目のビットを反転して、それを新しい文字列の 2 番目のビットとして使用し、リストの最後に到達するまでこれを繰り返します。ビット演算を逆にすることで、新しい文字列が元のリスト内のすべての文字列と少なくとも 1 位置異なっていることが保証されます。 (文字列のリスト内で対角線も形成するため、対角証明と呼ばれます。) #対角証明では、リスト内の各項目を順番にチェックするだけです。 . 文字列内の 1 ビットなので、通常は他のメソッドよりもはるかに高速ですが、その真の威力は無限に長い文字列の問題をいかにうまく処理できるかにあります。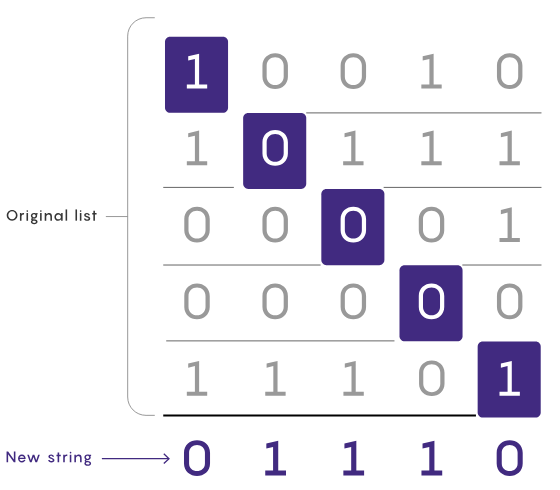 MIT の理論コンピューター科学者であるライアン ウィリアムズは、「文字列とリストは無限になる可能性がありますが、対角化手法は依然として効果的です。」
MIT の理論コンピューター科学者であるライアン ウィリアムズは、「文字列とリストは無限になる可能性がありますが、対角化手法は依然として効果的です。」
ジョージ カンター エルは、これを最初に利用しました。権力の権威であり、集合論という数学分野の創始者でした。 1873 年、彼は対角線を使用して、一部の無限値が他の値よりも大きいことを示しました。 60 年後、チューリングは、あるクラスの数学的問題が存在することを証明するために、このバージョンの対角証明を計算理論に適用しました。どのようなアルゴリズムでも解決することは不可能であるとチューリングは理論を提案しました。このタイプの問題には、明確に定義された入力と出力がありますが、入力を出力に変換するプロセスが定義されていません。チューリングは主に意思決定の問題に焦点を当て、この漠然とした課題をより具体的にしようと努めました。決定問題では、入力は 0 と 1 で構成される任意の文字列にすることができ、出力は 0 または 1 にすることができます
数値が素数 (1 とそれ自身でのみ割り切れる) かどうかの決定は決定です。問題は、数値を表す入力文字列が与えられた場合、その数値が素数であれば正しい出力は 1 であり、素数でない場合は 0 であるということです。別の例は、コンピューター プログラムの構文エラーをチェックすることです。入力文字列は、さまざまなプログラムのコードを表します。すべてのプログラムは、コンピューター上で保存および実行される方法であるため、この方法で表すことができます。ルールは、コードに構文エラーが含まれている場合は 1 を出力し、そうでない場合は 1 を出力します。 0を出力します。
アルゴリズムがすべての可能な入力に対して正しい出力を生成する場合にのみ、そのアルゴリズムは問題を解決したと言えます。一度でも失敗した場合、そのアルゴリズムは問題を解決するための一般的なアルゴリズムではありません。通常、解決したい問題を指定し、それを解決するためのアルゴリズムを見つけようとします。チューリングは、解決不可能な問題を探すときに、この論理をひっくり返しました。彼は、考えられるすべてのアルゴリズムの無限のリストを想像し、対角化を使用して、リスト上のすべてのアルゴリズムに対抗するパズルを構築しました。
20 個の質問からなる新しい質問を想像してください。回答者は、特定の概念から始めるのではなく、質問ごとに順番に不満の例を考え出します。ゲームが終了すると、解答者は、質問の反対の内容から完全に構成される命題を説明しました。
チューリングの対角証明プロセスでは、無限に長いアルゴリズムのリスト内の各アルゴリズムを実行します。思考: 「このアルゴリズムは問題を解決できるか?」計算不可能であることを証明したい問題は?」という、ゲームのコンテストのようなものです。ウィリアムズ氏は、「この方法は、元の問題を『無限問題』に変換します。」
ゲームに勝つために、チューリングは、各アルゴリズムによって与えられる答えが次の数になる質問を設計する必要があります。これは、最初のアルゴリズムで間違った答えを出力した特定の入力、2 番目のアルゴリズムを失敗させた別の入力などを見つけることを意味します。彼は、これらの特別な入力が、クルト・ゲーデルが少し前に「この命題は証明できない」のような自己言及的主張が数学の基礎に問題を引き起こす可能性があることを示したときに使用した方法と同様の方法を使用していることを発見しました。
ここで重要なのは、すべてのアルゴリズム (またはプログラム) は 0 と 1 の文字列として表現できるということです。これは、エラー チェッカーの例と同様に、アルゴリズムが別のアルゴリズムのエンコードを入力として受け取ることができることを意味します。原則として、アルゴリズムは独自のエンコーディングを入力として受け取ることもできます。
このようにして、チューリングの証明で述べた問題と同じように、計算不可能な問題を定義できます。「アルゴリズムのコードを表す入力文字列が与えられたとき、アルゴリズム自体のコードが入力として与えられたとき、アルゴリズムが 0 を出力する場合は 1 を出力し、そうでない場合は 0 を出力します。」 この問題を解決しようとするすべてのアルゴリズムは、少なくとも 1 つの入力、つまり独自のコードに対応する入力で誤った出力を生成します。これは、この異常な問題はどのアルゴリズムでも解決できないことを意味します
証明できないことは矛盾による証明です
コンピューター科学者による対角証明の使用はここで終わりではありません。 仕上げる。 1965 年、ジュリス ハートマニスとリチャード スターンズはチューリングの議論を応用して、すべての計算可能な問題が等しいわけではなく、本質的に他の問題よりも難しい問題があることを示しました。この結果は、計算問題の難しさの研究である計算複雑性理論の分野を開始しました。
複雑性理論の発展により、チューリングの対角証明の限界が明らかになりました。 1975 年、Baker、Gill、Solovy は、複雑性理論の多くの未解決問題が対角化だけでは解決できないことを示しました。その中で最も重要なのは有名な P/NP 問題です。これは、解の正しさが多項式時間で検証できるかどうか、また多項式時間で解けるかどうかに関する単純な問題です。
対角線の証明 限界これらは、それを非常に強力なものにする高度な抽象化の直接の結果です。チューリングの証明は、実際に発生する可能性のある計算不可能な問題にはまったく対処していません。代わりに、問題は抽象的な傾向があります。他の対角線も同様に現実世界から遠く離れていることが判明するため、現実世界の問題を解決することはできません。
ウィリアムズは、「対角証明は、グローブ ボックスで実験を行うのと同じように、問題自体には直接触れません。」
対角証明の減少傾向は、P を解くことが困難であることを示しています。 /NP 問題は長い道のりになるでしょう。限界があるにもかかわらず、対角証明は依然として複雑理論家の武器の重要なツールの 1 つです。 2011 年、ウィリアムズはこれを他のさまざまな手法と組み合わせて、制限された計算モデルではいくつかの信じられないほど難しい問題を解決できないことを実証しました。その結果、研究者を 25 年間悩ませてきた問題が解決されました。これは P/NP 問題の解決にはほど遠いものの、それでも大きな進歩を示しています。
何かが不可能であることを証明したい場合は、否定の力を過小評価しないでください。
元のリンク:
書き直す必要があります。内容は: https://www.quantamagazine.org/alan-turing-and-the-power-of-negative- Thinking-20230905/
以上がチューリングの原理を再考し、矛盾による証明の力を感じてください。の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7725
7725
 15
15
 1643
1643
 14
14
 1397
1397
 52
52
 1290
1290
 25
25
 1233
1233
 29
29
 パデュー大学による、時間をかける価値のある拡散モデルのチュートリアル
Apr 07, 2024 am 09:01 AM
パデュー大学による、時間をかける価値のある拡散モデルのチュートリアル
Apr 07, 2024 am 09:01 AM
拡散はより良いものを模倣するだけでなく、「創造」することもできます。拡散モデル(DiffusionModel)は、画像生成モデルである。 AI 分野でよく知られている GAN や VAE などのアルゴリズムと比較すると、拡散モデルは異なるアプローチを採用しており、その主な考え方は、最初に画像にノイズを追加し、その後徐々にノイズを除去するプロセスです。ノイズを除去して元の画像を復元する方法は、アルゴリズムの中核部分です。最後のアルゴリズムは、ランダムなノイズを含む画像から画像を生成できます。近年、生成 AI の驚異的な成長により、テキストから画像への生成、ビデオ生成など、多くのエキサイティングなアプリケーションが可能になりました。これらの生成ツールの背後にある基本原理は、以前の方法の制限を克服する特別なサンプリング メカニズムである拡散の概念です。
 ワンクリックでPPTを生成!キミ: まずは「PPT出稼ぎ労働者」を普及させましょう
Aug 01, 2024 pm 03:28 PM
ワンクリックでPPTを生成!キミ: まずは「PPT出稼ぎ労働者」を普及させましょう
Aug 01, 2024 pm 03:28 PM
キミ: たった 1 文の PPT がわずか 10 秒で完成します。 PPTはとても面倒です!会議を開催するには PPT が必要であり、週次報告書を作成するには PPT が必要であり、投資を勧誘するには PPT を提示する必要があり、不正行為を告発するには PPT を送信する必要があります。大学は、PPT 専攻を勉強するようなものです。授業中に PPT を見て、授業後に PPT を行います。おそらく、デニス オースティンが 37 年前に PPT を発明したとき、PPT がこれほど普及する日が来るとは予想していなかったでしょう。 PPT 作成の大変な経験を話すと涙が出ます。 「20 ページを超える PPT を作成するのに 3 か月かかり、何十回も修正しました。PPT を見ると吐きそうになりました。」 「ピーク時には 1 日に 5 枚の PPT を作成し、息をすることさえありました。」 PPTでした。」 即席の会議をするなら、そうすべきです
 CVPR 2024 のすべての賞が発表されました!オフラインでのカンファレンスには1万人近くが参加し、Googleの中国人研究者が最優秀論文賞を受賞した
Jun 20, 2024 pm 05:43 PM
CVPR 2024 のすべての賞が発表されました!オフラインでのカンファレンスには1万人近くが参加し、Googleの中国人研究者が最優秀論文賞を受賞した
Jun 20, 2024 pm 05:43 PM
北京時間6月20日早朝、シアトルで開催されている最高の国際コンピュータビジョンカンファレンス「CVPR2024」が、最優秀論文やその他の賞を正式に発表した。今年は、最優秀論文 2 件と学生優秀論文 2 件を含む合計 10 件の論文が賞を受賞しました。また、最優秀論文ノミネートも 2 件、学生優秀論文ノミネートも 4 件ありました。コンピュータービジョン (CV) 分野のトップカンファレンスは CVPR で、毎年多数の研究機関や大学が集まります。統計によると、今年は合計 11,532 件の論文が投稿され、2,719 件が採択され、採択率は 23.6% でした。ジョージア工科大学による CVPR2024 データの統計分析によると、研究テーマの観点から最も論文数が多いのは画像とビデオの合成と生成です (Imageandvideosyn
 PyCharm Community Edition インストール ガイド: すべての手順をすばやくマスターする
Jan 27, 2024 am 09:10 AM
PyCharm Community Edition インストール ガイド: すべての手順をすばやくマスターする
Jan 27, 2024 am 09:10 AM
PyCharm コミュニティ版のクイック スタート: 詳細なインストール チュートリアル 完全な分析 はじめに: PyCharm は、開発者が Python コードをより効率的に作成できるようにする包括的なツール セットを提供する強力な Python 統合開発環境 (IDE) です。この記事では、PyCharm Community Edition のインストール方法を詳しく紹介し、初心者がすぐに使い始めるのに役立つ具体的なコード例を示します。ステップ 1: PyCharm Community Edition をダウンロードしてインストールする PyCharm を使用するには、まず公式 Web サイトからダウンロードする必要があります
 ベアメタルから 700 億のパラメータを備えた大規模モデルまで、チュートリアルとすぐに使えるスクリプトがここにあります
Jul 24, 2024 pm 08:13 PM
ベアメタルから 700 億のパラメータを備えた大規模モデルまで、チュートリアルとすぐに使えるスクリプトがここにあります
Jul 24, 2024 pm 08:13 PM
LLM が大量のデータを使用して大規模なコンピューター クラスターでトレーニングされていることはわかっています。このサイトでは、LLM トレーニング プロセスを支援および改善するために使用される多くの方法とテクノロジが紹介されています。今日、私たちが共有したいのは、基礎となるテクノロジーを深く掘り下げ、オペレーティング システムさえ持たない大量の「ベア メタル」を LLM のトレーニング用のコンピューター クラスターに変える方法を紹介する記事です。この記事は、機械がどのように考えるかを理解することで一般的な知能の実現に努めている AI スタートアップ企業 Imbue によるものです。もちろん、オペレーティング システムを持たない大量の「ベア メタル」を LLM をトレーニングするためのコンピューター クラスターに変換することは、探索と試行錯誤に満ちた簡単なプロセスではありませんが、Imbue は最終的に 700 億のパラメータを備えた LLM のトレーニングに成功しました。プロセスが蓄積する
 C言語学習を始めるためのプログラミングソフト5選
Feb 19, 2024 pm 04:51 PM
C言語学習を始めるためのプログラミングソフト5選
Feb 19, 2024 pm 04:51 PM
C言語は広く使われているプログラミング言語であり、コンピュータプログラミングを志す人にとって必ず学ばなければならない基本的な言語の一つです。ただし、初心者にとって、特に関連する学習ツールや教材が不足しているため、新しいプログラミング言語を学習するのは難しい場合があります。この記事では、C言語初心者がすぐに始められるプログラミングソフトを5つ紹介します。最初のプログラミング ソフトウェアは Code::Blocks でした。 Code::Blocks は、無料のオープンソース統合開発環境 (IDE) です。
 AIの活用 | AIが一人暮らしの女の子の生活ビデオブログを作成、3日間で数万件の「いいね!」を獲得
Aug 07, 2024 pm 10:53 PM
AIの活用 | AIが一人暮らしの女の子の生活ビデオブログを作成、3日間で数万件の「いいね!」を獲得
Aug 07, 2024 pm 10:53 PM
Machine Power Report 編集者: Yang Wen 大型モデルや AIGC に代表される人工知能の波は、私たちの生活や働き方を静かに変えていますが、ほとんどの人はまだその使い方を知りません。そこで、直感的で興味深く、簡潔な人工知能のユースケースを通じてAIの活用方法を詳しく紹介し、皆様の思考を刺激するコラム「AI in Use」を立ち上げました。また、読者が革新的な実践的な使用例を提出することも歓迎します。ビデオリンク: https://mp.weixin.qq.com/s/2hX_i7li3RqdE4u016yGhQ 最近、Xiaohongshu で一人暮らしの女の子の生活 vlog が人気になりました。イラスト風のアニメーションといくつかの癒しの言葉を組み合わせれば、数日で簡単に習得できます。
 技術初心者必読:C言語とPythonの難易度分析
Mar 22, 2024 am 10:21 AM
技術初心者必読:C言語とPythonの難易度分析
Mar 22, 2024 am 10:21 AM
タイトル: 技術初心者必読: 具体的なコード例を必要とする C 言語と Python の難易度分析 今日のデジタル時代において、プログラミング技術はますます重要な能力となっています。ソフトウェア開発、データ分析、人工知能などの分野で働きたい場合でも、単に興味があってプログラミングを学びたい場合でも、適切なプログラミング言語を選択することが最初のステップです。数あるプログラミング言語の中でも、C言語とPythonは広く使われているプログラミング言語であり、それぞれに独自の特徴があります。この記事ではC言語とPythonの難易度を分析します。




