混合ガウスモデルを使用した多峰性分布の分解

混合ガウス モデルを使用して、一次元の多峰性分布を複数の分布に分割します

混合ガウス モデル (混合ガウス モデル) (略して GMM) は、複雑なデータ分布をモデル化および分析するために統計および機械学習の分野で一般的に使用される確率モデルです。 GMM は、観測データが複数のガウス分布で構成され、各ガウス分布がコンポーネントと呼ばれ、これらのコンポーネントが重みによってデータへの寄与を制御すると仮定する生成モデルです。

マルチモーダル分布でデータを生成する

データ セットに複数の異なるピークまたはモードが表示される場合、通常は、複数の顕著なクラスターがあることを意味します。またはデータセット内のデータポイントの集中。各モードは、分布内の顕著なクラスターまたはデータ ポイントの集中を表し、データ値が発生する可能性がより高い高密度領域と考えることができます。 numpy で生成された 1 次元の配列。

import numpy as np  dist_1 = np.random.normal(10, 3, 1000) dist_2 = np.random.normal(30, 5, 4000) dist_3 = np.random.normal(45, 6, 500)  multimodal_dist = np.concatenate((dist_1, dist_2, dist_3), axis=0)

一次元のデータ分布を視覚化してみましょう。

import matplotlib.pyplot as plt import seaborn as sns sns.set_style('whitegrid')  plt.hist(multimodal_dist, bins=50, alpha=0.5) plt.show()

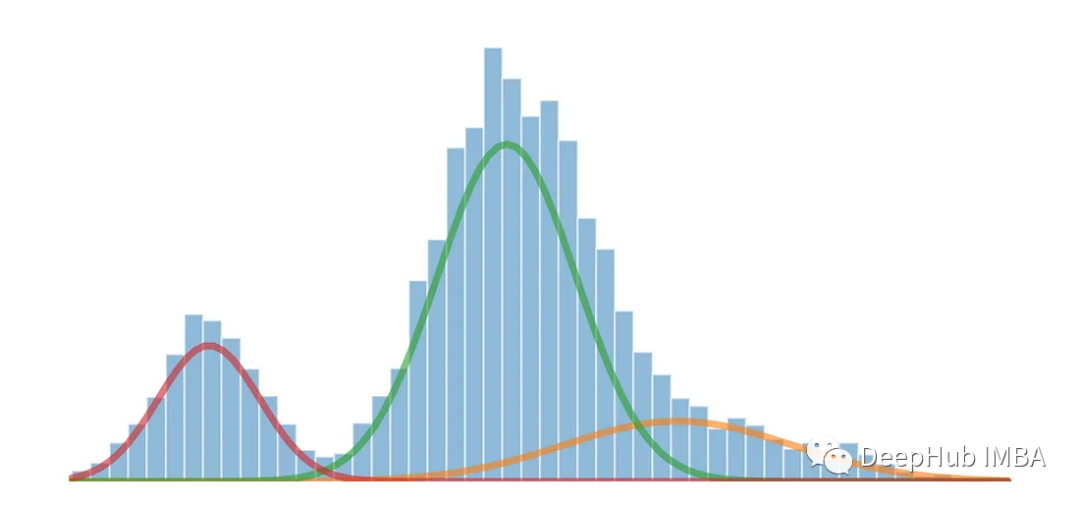
混合ガウス モデルを使用したマルチモーダル分布の分割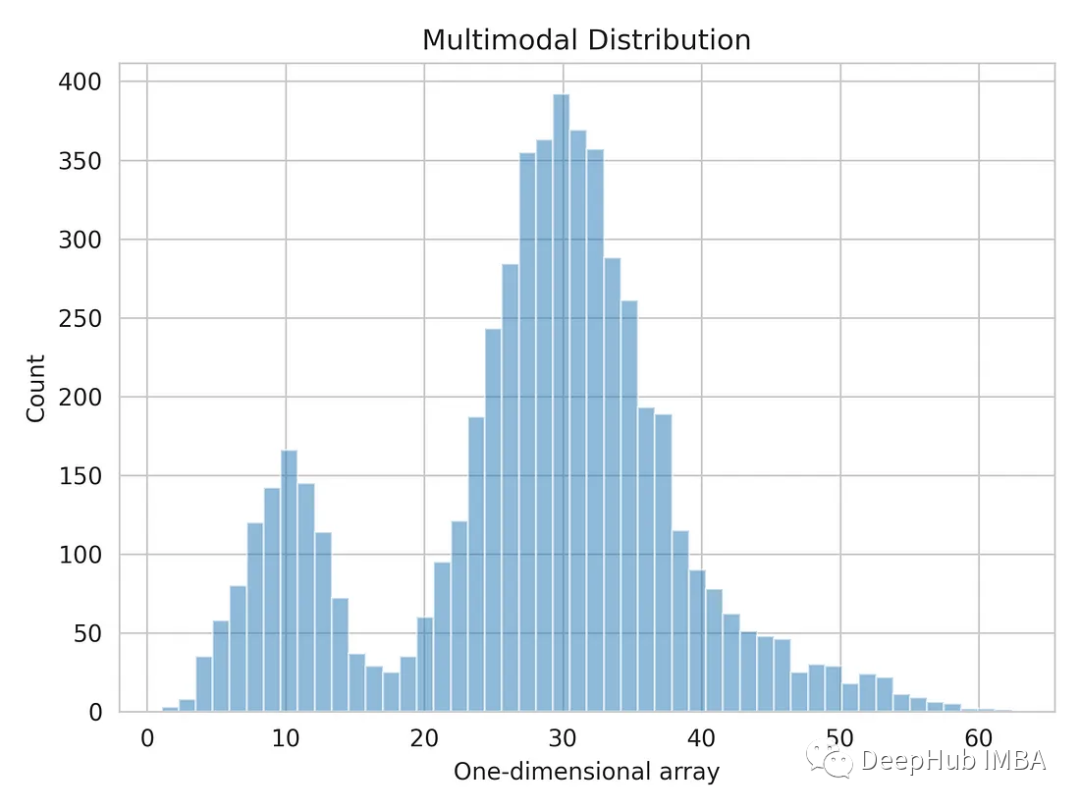

混合ガウス モデルを使用して、各分布の平均と標準偏差を計算し、多峰性分布を 3 つの元の分布に分離します。混合ガウス モデルは、データ クラスタリングに使用できる教師なし確率モデルです。期待値最大化アルゴリズムを使用して密度領域を推定します

from sklearn.mixture import GaussianMixture  gmm = GaussianMixture(n_compnotallow=3) gmm.fit(multimodal_dist.reshape(-1, 1))  means = gmm.means_  # Conver covariance into Standard Deviation standard_deviations = gmm.covariances_**0.5  # Useful when plotting the distributions later weights = gmm.weights_   print(f"Means: {means}, Standard Deviations: {standard_deviations}")  #Means: [29.4, 10.0, 38.9], Standard Deviations: [4.6, 3.1, 7.9]

すでに平均と標準偏差が得られており、元の分布をモデル化できます。平均値と標準偏差は正確には正確ではないかもしれませんが、おおよその推定値が得られることがわかります。

推定値を元のデータと比較してください。

from scipy.stats import norm  fig, axes = plt.subplots(nrows=3, ncols=1, sharex='col', figsize=(6.4, 7))  for bins, dist in zip([14, 34, 26], [dist_1, dist_2, dist_3]):axes[0].hist(dist, bins=bins, alpha=0.5)  axes[1].hist(multimodal_dist, bins=50, alpha=0.5)  x = np.linspace(min(multimodal_dist), max(multimodal_dist), 100)  for mean, covariance, weight in zip(means, standard_deviations, weights):pdf = weight*norm.pdf(x, mean, std)plt.plot(x.reshape(-1, 1), pdf.reshape(-1, 1), alpha=0.5)  plt.show()

概要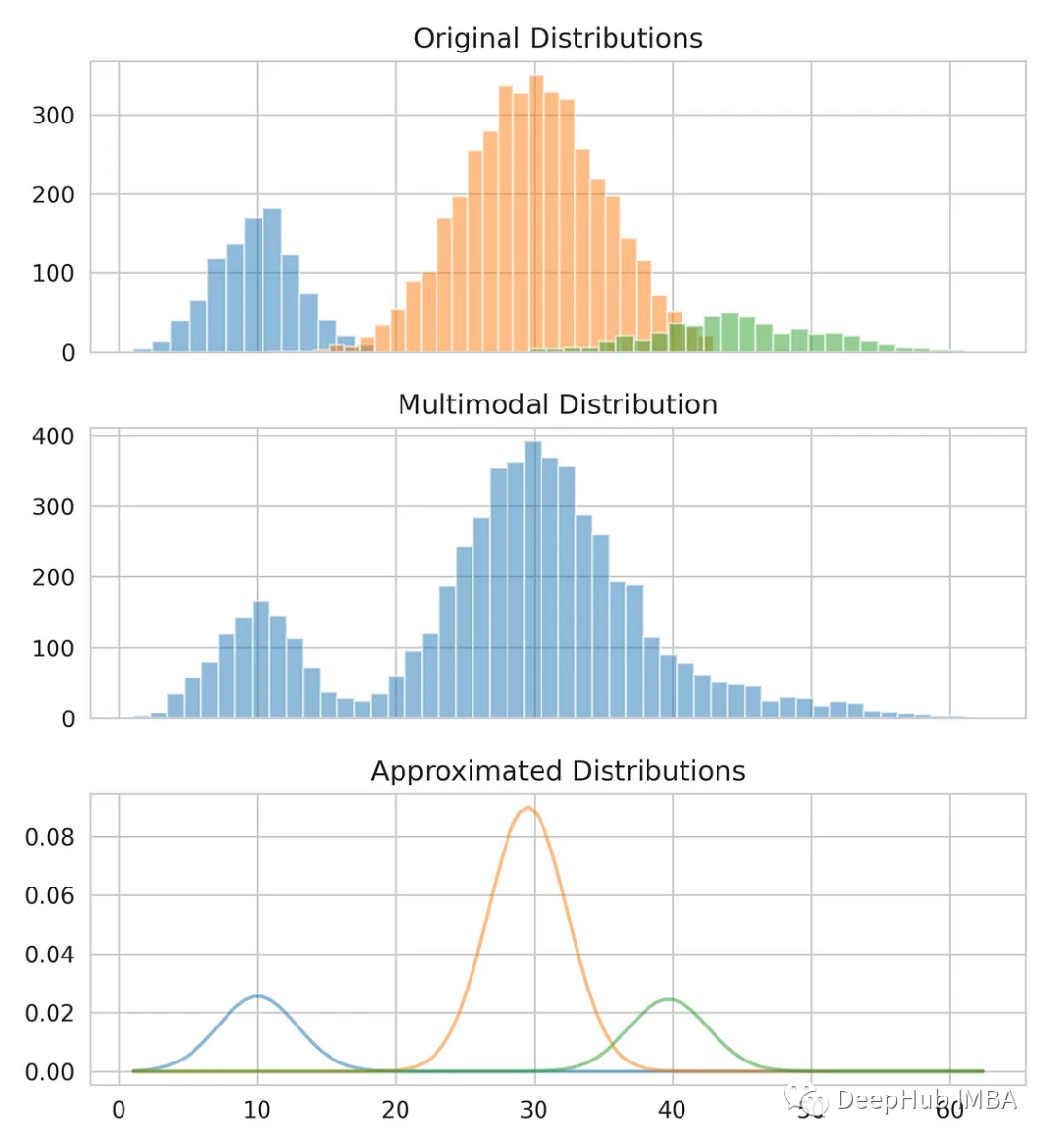

混合ガウス モデルは、複雑なデータの分析に使用できる強力なツールです。データ分布のモデル化と分析に使用され、多くの機械学習アルゴリズムの基礎の 1 つでもあります。これには幅広い用途があり、さまざまなデータ モデリングや分析の問題を解決できます。

このメソッドは、特徴量エンジニアリング手法として使用して、部分分布の信頼区間を推定できます。入力変数

以上が混合ガウスモデルを使用した多峰性分布の分解の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。