より多用途かつ効果的な、Ant の自社開発オプティマイザー WSAM が KDD Oral に採用されました
ディープ ニューラル ネットワーク (DNN) の汎化能力は、極値点の平坦性に密接に関係しているため、より平坦な極点を見つけて汎化能力を向上させるために、Sharpness-Aware Minimization (SAM) アルゴリズムが登場しました。 。この論文では、SAM の損失関数を再検討し、平坦性を正則化項として使用することでトレーニング極点の平坦性を改善する、より一般的で効果的な方法 WSAM を提案します。さまざまな公開データセットでの実験では、元のオプティマイザーである SAM およびそのバリアントと比較して、WSAM がほとんどの場合で優れた汎化パフォーマンスを達成することが示されています。 WSAM は、Ant の社内デジタル決済、デジタル金融、その他のシナリオでも広く採用されており、目覚ましい成果を上げています。この論文はKDD '23に口頭論文として受理されました。

- 論文アドレス: https: / /arxiv.org/pdf/2305.15817.pdf
- コードアドレス: https://github.com/intelligent-machine-learning/dlrover/tree/master /atorch/atorch/optimizers
#深層学習テクノロジーの発展に伴い、CV や NLP などのさまざまな機械学習シナリオで高度に過剰パラメータ化された DNN が使用されています。 . 大成功でした。過剰にパラメータ化されたモデルはトレーニング データを過剰適合する傾向がありますが、通常は優れた汎化機能を備えています。一般化の秘密はますます注目を集めており、深層学習の分野で人気の研究トピックとなっています。
最新の研究では、一般化能力が極点の平坦度と密接に関係していることが示されています。言い換えれば、損失関数の「ランドスケープ」に平坦な極点が存在することで、汎化誤差が小さくなる可能性があります。 Sharpness-Aware Minimization (SAM) [1] は、平坦な極点を見つけるための手法であり、現在最も有望な技術方向の 1 つであると考えられています。 SAM テクノロジーは、コンピューター ビジョン、自然言語処理、2 層学習などの多くの分野で広く使用されており、これらの分野における以前の最先端の手法を大幅に上回っています
より平坦な の最小値を探索するために、SAM は w における損失関数 L の平坦性を次のように定義します。
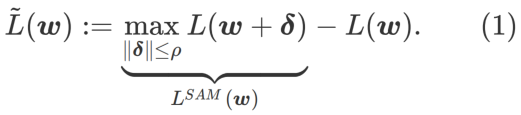
GSAM [2] は、 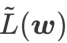 が局所極点におけるヘッセ行列の最大固有値の近似値であることを証明し、 が実際に平坦度 (急峻さ) の有効な尺度であることを示しています。ただし、
が局所極点におけるヘッセ行列の最大固有値の近似値であることを証明し、 が実際に平坦度 (急峻さ) の有効な尺度であることを示しています。ただし、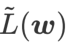 は最小点ではなく平坦な領域を見つけるためにのみ使用できるため、損失関数が (周囲の領域は平坦であるにもかかわらず) 損失値がまだ大きい点に収束する可能性があります。したがって、SAM は
は最小点ではなく平坦な領域を見つけるためにのみ使用できるため、損失関数が (周囲の領域は平坦であるにもかかわらず) 損失値がまだ大きい点に収束する可能性があります。したがって、SAM は 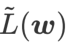
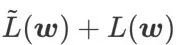 、つまり
、つまり 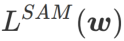 を損失関数として使用します。これは、より平坦な表面を見つけることと、 と
を損失関数として使用します。これは、より平坦な表面を見つけることと、 と 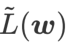
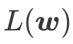 の間でより小さい損失値を見つけることとの間の妥協点と見なすことができ、両方に同じ重みが与えられます。
の間でより小さい損失値を見つけることとの間の妥協点と見なすことができ、両方に同じ重みが与えられます。
この記事では、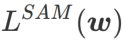 の構造を再考し、
の構造を再考し、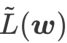 を正則化用語とみなします。私たちは、WSAM (Weighted Sharpness-Aware Minimization) と呼ばれる、より一般的で効果的なアルゴリズムを開発しました。このアルゴリズムの損失関数は、重み付き平坦性項
を正則化用語とみなします。私たちは、WSAM (Weighted Sharpness-Aware Minimization) と呼ばれる、より一般的で効果的なアルゴリズムを開発しました。このアルゴリズムの損失関数は、重み付き平坦性項 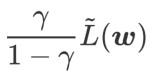 を通常の項として追加し、ハイパーパラメータ
を通常の項として追加し、ハイパーパラメータ 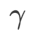 平面度の重みを制御します。手法の紹介の章では、
平面度の重みを制御します。手法の紹介の章では、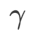 を使用して損失関数をガイドし、より平坦な、またはより小さい極値点を見つける方法を説明しました。私たちの主な貢献は次のように要約できます。
を使用して損失関数をガイドし、より平坦な、またはより小さい極値点を見つける方法を説明しました。私たちの主な貢献は次のように要約できます。
- 我々は、平坦性を正則化項として扱い、異なるタスク間で異なる重みを与える WSAM を提案します。現在のステップの平坦性を正確に反映することを目的として、更新式の正則化項を処理する「重みデカップリング」手法を提案します。基礎となるオプティマイザーが SGD ではない場合 (SGDM や Adam など)、WSAM の形式は SAM とは大きく異なります。アブレーション実験では、この技術によりほとんどの場合のパフォーマンスが向上することが示されています。
- 公開データセットの一般的なタスクにおける WSAM の有効性を検証しました。実験結果は、SAM およびそのバリアントと比較して、ほとんどの状況で WSAM の汎化パフォーマンスが優れていることを示しています。
予備知識
SAMとは、式(1)で定義される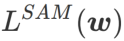 のミニマックス最適化問題を解く技術です。
のミニマックス最適化問題を解く技術です。
まず、SAM は、w の周りの一次テイラー展開を使用して、内層の最大化問題、つまり 、
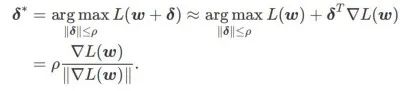 を近似します。
を近似します。
##2 番目に、SAM は の近似勾配を採用することで w を更新します。つまり、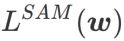
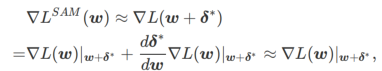
2 番目の近似は次のとおりです。加速度を計算します。他の勾配ベースのオプティマイザー (ベース オプティマイザーと呼ばれる) は、SAM の一般的なフレームワークに組み込むことができます。詳細については、アルゴリズム 1 を参照してください。アルゴリズム 1 の 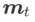 と
と 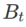 を変更すると、SGD、SGDM、Adam などのさまざまな基本オプティマイザーを取得できます (表 1 を参照)。基本オプティマイザーが SGD の場合、アルゴリズム 1 は SAM 論文 [1] の元の SAM にフォールバックすることに注意してください。
を変更すると、SGD、SGDM、Adam などのさまざまな基本オプティマイザーを取得できます (表 1 を参照)。基本オプティマイザーが SGD の場合、アルゴリズム 1 は SAM 論文 [1] の元の SAM にフォールバックすることに注意してください。


##WSAM の設計詳細
ここでは、規則的な損失と平坦性の項で構成される
の正式な定義を示します。式 (1) から、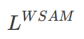
=0 の場合、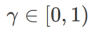 は通常の損失に退化します。
は通常の損失に退化します。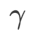 =1/2 の場合、
=1/2 の場合、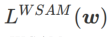 は # と等価です。 ## ;
は # と等価です。 ## ; 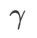 >1/2 の場合、 は平坦度をより重視するため、SAM と比較して損失値が小さいよりも曲率が小さい点を見つけやすくなり、その逆も同様です。 ; 同じく。
>1/2 の場合、 は平坦度をより重視するため、SAM と比較して損失値が小さいよりも曲率が小さい点を見つけやすくなり、その逆も同様です。 ; 同じく。 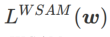
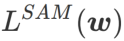
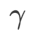 さまざまな基本オプティマイザーを含む WSAM の一般的なフレームワークは、さまざまな
さまざまな基本オプティマイザーを含む WSAM の一般的なフレームワークは、さまざまな 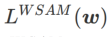 および
および
を選択することで実装できます。「アルゴリズム」を参照してください。 2.たとえば、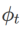 と
と 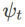 の場合、基本オプティマイザーが SGD である WSAM が得られます。アルゴリズム 3 を参照してください。ここでは、「重みデカップリング」手法を採用します。つまり、 平坦性項は、勾配の計算と重みの更新のために基本オプティマイザーと統合されず、独立して計算されます (アルゴリズム 2 の 7 行目の最後の項)。このように、正則化の効果は、追加情報なしで現在のステップの平坦性のみを反映します。比較のために、アルゴリズム 4 では、「重みデカップリング」を行わない WSAM (Coupled-WSAM と呼ばれる) が得られます。たとえば、基礎となるオプティマイザが SGDM である場合、結合 WSAM の正則化項は平坦性の指数移動平均です。実験セクションで示したように、「重みデカップリング」により、ほとんどの場合、汎化パフォーマンスが向上します。
の場合、基本オプティマイザーが SGD である WSAM が得られます。アルゴリズム 3 を参照してください。ここでは、「重みデカップリング」手法を採用します。つまり、 平坦性項は、勾配の計算と重みの更新のために基本オプティマイザーと統合されず、独立して計算されます (アルゴリズム 2 の 7 行目の最後の項)。このように、正則化の効果は、追加情報なしで現在のステップの平坦性のみを反映します。比較のために、アルゴリズム 4 では、「重みデカップリング」を行わない WSAM (Coupled-WSAM と呼ばれる) が得られます。たとえば、基礎となるオプティマイザが SGDM である場合、結合 WSAM の正則化項は平坦性の指数移動平均です。実験セクションで示したように、「重みデカップリング」により、ほとんどの場合、汎化パフォーマンスが向上します。 
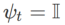
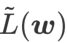

 #
#
図 1 は、さまざまな 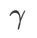 値での WSAM 更新プロセスを示しています。
値での WSAM 更新プロセスを示しています。 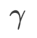 の場合、
の場合、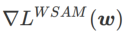 が
が 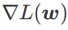 と
と 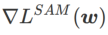 の間にあり、## となります。 # が増加すると、徐々に
の間にあり、## となります。 # が増加すると、徐々に 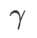
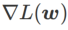 から外れます。
から外れます。

簡単な例
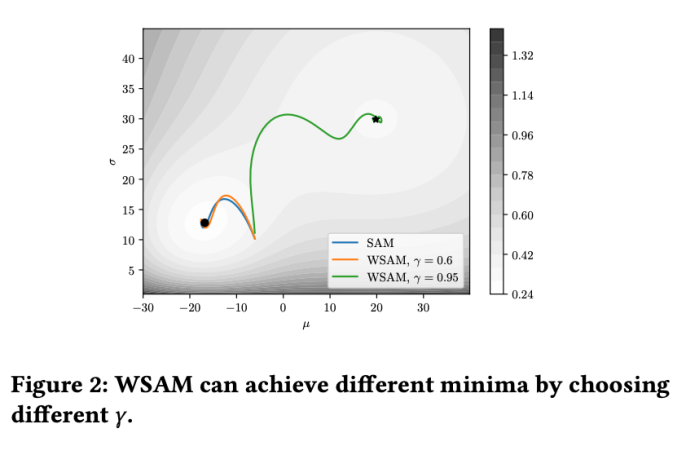
WSAM における γ の効果と利点をよりよく説明するために、次のようにします。 set これは簡単な 2 次元の例です。図 2 に示すように、損失関数には、左下隅に比較的不均一な極点 (位置: (-16.8, 12.8)、損失値: 0.28) があり、右上隅に平坦な極点 (位置: (19.8、29.9)、損失値: 0.36)。損失関数は次のように定義されます: 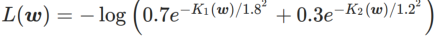 、ここで
、ここで 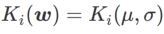 は、単変量ガウス モデルと 2 つの正規分布の間の KL 発散、つまり です。
は、単変量ガウス モデルと 2 つの正規分布の間の KL 発散、つまり です。 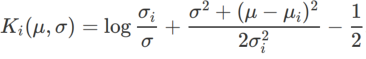 、ここで
、ここで 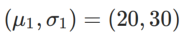 と
と 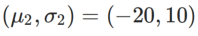 。
。
ベース オプティマイザーとしてモーメンタム 0.9 の SGDM を使用し、SAM と WSAM に 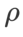 =2 を設定します。損失関数は、初期点 (-6、10) から開始して、学習率 5 を使用して 150 ステップで最適化されます。 SAM は、損失値がより低いもののより不均一になる極点に収束します。
=2 を設定します。損失関数は、初期点 (-6、10) から開始して、学習率 5 を使用して 150 ステップで最適化されます。 SAM は、損失値がより低いもののより不均一になる極点に収束します。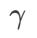 =0.6 の WSAM も同様です。ただし、#=0.95 では、損失関数が平坦な極値点に収束します。これは、より強力な平坦性正則化が役割を果たしていることを示しています。
=0.6 の WSAM も同様です。ただし、#=0.95 では、損失関数が平坦な極値点に収束します。これは、より強力な平坦性正則化が役割を果たしていることを示しています。 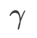
WSAM の有効性を検証するために、さまざまなタスクについて実験を実施しました。
画像分類
最初に、Cifar10 および Cifar100 データセットでトレーニング モデルに対する WSAM の効果を最初から調査しました。私たちが選択したモデルには、ResNet18 と WideResNet-28-10 が含まれます。 ResNet18 と WideResNet-28-10 に対してそれぞれ 128、256 の事前定義されたバッチ サイズを使用して、Cifar10 と Cifar100 でモデルをトレーニングします。ここで使用される基本オプティマイザーは、モーメンタム 0.9 の SGDM です。 SAM [1] の設定に従って、各基本オプティマイザーは SAM クラス オプティマイザーの 2 倍のエポック数を実行します。両方のモデルを 400 エポック (SAM クラス オプティマイザーの場合は 200 エポック) トレーニングし、コサイン スケジューラーを使用して学習率を下げました。ここでは、カットアウトや自動拡張などの他の高度なデータ拡張方法は使用しません。
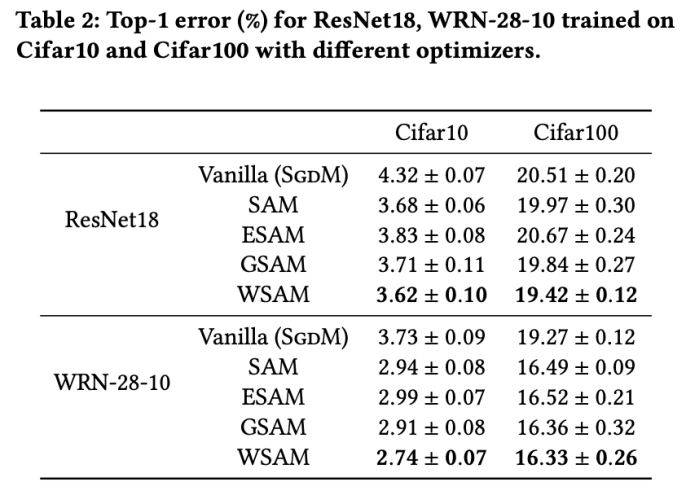
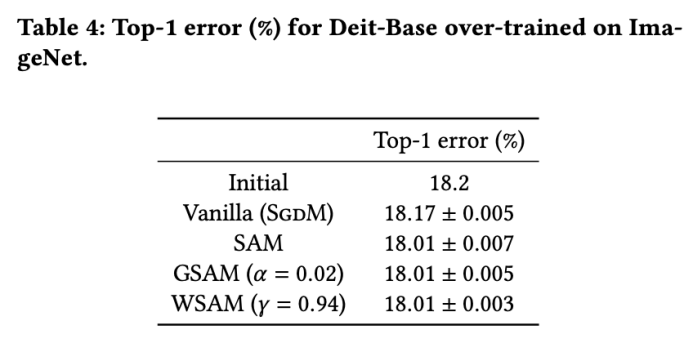
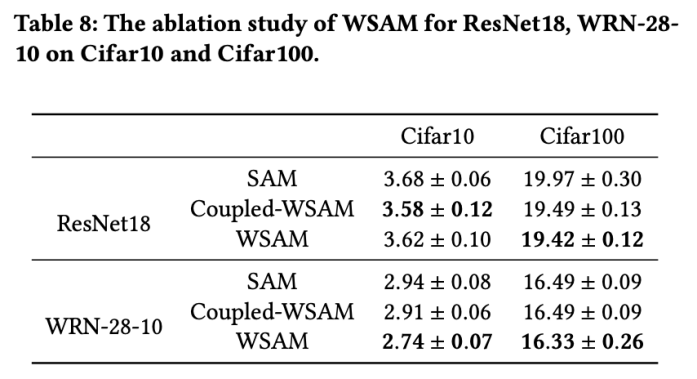
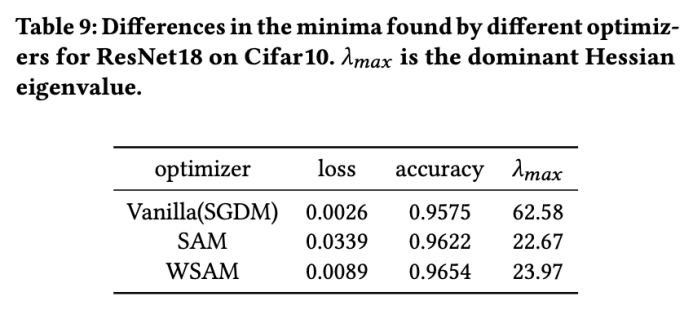
両方のモデルで、ジョイント グリッド検索を使用して基本オプティマイザーの学習率と重み減衰係数を決定し、次の SAM のようなオプティマイザー実験でそれらを一定に保ちます。学習率と重み減衰係数の検索範囲はそれぞれ {0.05, 0.1} と {1e-4, 5e-4, 1e-3} です。すべての SAM クラス オプティマイザーにはハイパーパラメーター 表 2 は、さまざまなオプティマイザーでの Cifar10 および Cifar100 での ResNet18 および WRN-28-10 のトップテスト結果を示しています (エラー率 1)。 SAM クラス オプティマイザーは、基本オプティマイザーと比較してパフォーマンスが大幅に向上すると同時に、WSAM は他の SAM クラス オプティマイザーよりも大幅に優れています。 ImageNet データセットの Transformers ネットワークで Data-Efficient Image をさらに使用します実験用の構造。事前にトレーニングされた DeiT ベースのチェックポイントを再開し、3 エポックの間トレーニングを続けます。モデルはバッチ サイズ 256 を使用してトレーニングされ、基本オプティマイザーは運動量 0.9 の SGDM、重み減衰係数は 1e-4、学習率は 1e-5 です。 4 枚のカード NVIDIA A100 GPU で実行を 5 回繰り返し、平均誤差と標準偏差を計算しました。 {0.05, 0.1, 0.5, 1.0,⋯ , 6.0} 最高の モデルの最初のトップ 1 エラー率は 18.2% で、さらに 3 エポック後のエラー率を表 4 に示します。 3 つの SAM に似たオプティマイザー間に大きな違いは見つかりませんでしたが、いずれも基本オプティマイザーよりも優れたパフォーマンスを示し、より平坦な極点を見つけ、より優れた汎化機能を備えていることを示しています。 以前の研究 [1、4、5] で示されているように、SAM クラス オプティマイザーはトレーニング セットにラベル ノイズが存在する場合でも良好に機能します。優れた堅牢性を実現します。ここでは、WSAM の堅牢性を SAM、ESAM、GSAM と比較します。 Cifar10 データセット上で ResNet18 を 200 エポック間トレーニングし、ノイズ レベル 20%、40%、60%、80% の対称ラベル ノイズを注入します。基本オプティマイザーとして 0.9 の運動量、バッチ サイズ 128、学習率 0.05、重み減衰係数 1e-3、および学習率を減衰するコサイン スケジューラを持つ SGDM を使用します。各ラベル ノイズ レベルについて、範囲 {0.01, 0.02, 0.05, 0.1, 0.2, 0.5} 内の SAM でグリッド検索を実行し、共通の SAM クラス オプティマイザーは ASAM で使用できます [4 ] と SAM [5] などのフィッシャー技術を組み合わせて、探索された近傍の形状を適応的に調整します。 Cifar10 上の WRN-28-10 で実験を実施し、それぞれ適応情報法とフィッシャー情報法を使用した場合の SAM と WSAM のパフォーマンスを比較し、探査領域のジオメトリが SAM のようなオプティマイザーの一般化パフォーマンスにどのような影響を与えるかを理解します。 驚くべきことに、表 7 に示すように、ベースライン WSAM は複数の候補の間でもより優れた一般化を示しています。したがって、固定 このセクションでは、WSAM をより深く理解するためにアブレーション実験を実施します。 「重量デカップリング」テクノロジーの重要性。 WSAM の設計の詳細で説明したように、「重みデカップリング」なしの WSAM バリアント (アルゴリズム 4) 結合 WSAM を元の方式と比較します。 結果を表 8 に示します。ほとんどの場合、結合 WSAM は SAM よりも優れた結果を生成し、WSAM はほとんどの場合に結果をさらに改善し、「重みデカップリング」技術の有効性を示しています。 ここでは、WSAM オプティマイザーと SAM オプティマイザーによって検出された極点の違いを比較することで、WSAM オプティマイザーについての理解をさらに深めます。極点での平坦さ (急峻さ) は、ヘッセ行列の最大固有値によって説明できます。固有値が大きいほど、平坦ではなくなります。この最大固有値を計算するには、Power Iteration アルゴリズムを使用します。 表 9 は、SAM オプティマイザーと WSAM オプティマイザーによって検出された極値間の差異を示しています。バニラ オプティマイザーで見つかった極点は損失値が小さいものの平坦度が低いのに対し、SAM で見つかった極点は損失値が大きいものの平坦度が高く、汎化パフォーマンスが向上していることがわかります。興味深いことに、WSAM によって検出された極値ポイントは、SAM よりも損失値がはるかに小さいだけでなく、SAM に非常に近い平坦性も持っています。これは、極値点を見つけるプロセスにおいて、WSAM がより平坦な領域を検索しようとする一方で、より小さい損失値を確保することを優先していることを示しています。 SAM と比較して、WSAM には追加のハイパーパラメータ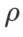 (近傍サイズ) があるため、次に SAM オプティマイザーで最適な
(近傍サイズ) があるため、次に SAM オプティマイザーで最適な 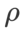 を検索し、他の SAM クラス オプティマイザーにも同じ値を使用します。
を検索し、他の SAM クラス オプティマイザーにも同じ値を使用します。 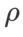 の検索範囲は {0.01, 0.02, 0.05, 0.1, 0.2, 0.5} です。最後に、他の SAM クラス オプティマイザーの固有のハイパーパラメーターを検索しました。検索範囲は、それぞれの元の記事の推奨範囲から得られました。 GSAM [2] の場合、{0.01, 0.02, 0.03, 0.1, 0.2, 0.3} の範囲で検索します。 ESAM [3] の場合、範囲 {0.4, 0.5, 0.6} 内の
の検索範囲は {0.01, 0.02, 0.05, 0.1, 0.2, 0.5} です。最後に、他の SAM クラス オプティマイザーの固有のハイパーパラメーターを検索しました。検索範囲は、それぞれの元の記事の推奨範囲から得られました。 GSAM [2] の場合、{0.01, 0.02, 0.03, 0.1, 0.2, 0.3} の範囲で検索します。 ESAM [3] の場合、範囲 {0.4, 0.5, 0.6} 内の  、範囲 {0.4, 0.5, 0.6} 内の
、範囲 {0.4, 0.5, 0.6} 内の 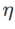 、および{0.4, 0.5, 0.6} の範囲内で
、および{0.4, 0.5, 0.6} の範囲内で  を検索します。 WSAM の場合、{0.5、0.6、0.7、0.8、0.82、0.84、0.86、0.88、0.9、0.92、0.94、0.96} の範囲で
を検索します。 WSAM の場合、{0.5、0.6、0.7、0.8、0.82、0.84、0.86、0.88、0.9、0.92、0.94、0.96} の範囲で  を検索します。異なるランダムシードを使用して実験を 5 回繰り返し、平均誤差と標準偏差を計算しました。シングルカードの NVIDIA A100 GPU で実験を行います。各モデルのオプティマイザのハイパーパラメータを表 3 にまとめます。
を検索します。異なるランダムシードを使用して実験を 5 回繰り返し、平均誤差と標準偏差を計算しました。シングルカードの NVIDIA A100 GPU で実験を行います。各モデルのオプティマイザのハイパーパラメータを表 3 にまとめます。 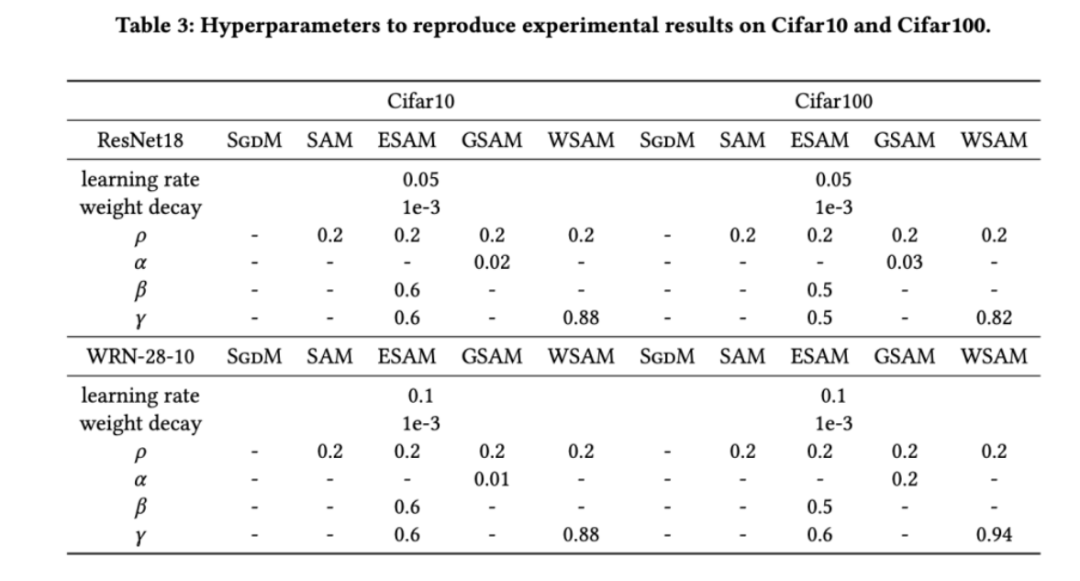
ImageNet に関する追加トレーニング
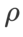 。最適な
。最適な 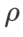 =5.5 は、他の SAM クラス オプティマイザーに直接使用されます。その後、{0.01, 0.02, 0.03, 0.1, 0.2, 0.3} で GSAM の最適な
=5.5 は、他の SAM クラス オプティマイザーに直接使用されます。その後、{0.01, 0.02, 0.03, 0.1, 0.2, 0.3} で GSAM の最適な  を検索し、ステップ サイズ 0.02 ## で 0.80 ~ 0.98 の範囲で WSAM の最適な WSAM を検索します。
を検索し、ステップ サイズ 0.02 ## で 0.80 ~ 0.98 の範囲で WSAM の最適な WSAM を検索します。 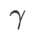 #。
#。 
ラベル ノイズに対する堅牢性
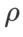 値を決定しました。次に、他のオプティマイザー固有のハイパーパラメーターを個別に検索して、最適な汎化パフォーマンスを見つけます。結果を再現するために必要なハイパーパラメータを表 5 に示します。表 6 に堅牢性テストの結果を示しますが、一般に WSAM は SAM、ESAM、GSAM よりも優れた堅牢性を持っています。
値を決定しました。次に、他のオプティマイザー固有のハイパーパラメーターを個別に検索して、最適な汎化パフォーマンスを見つけます。結果を再現するために必要なハイパーパラメータを表 5 に示します。表 6 に堅牢性テストの結果を示しますが、一般に WSAM は SAM、ESAM、GSAM よりも優れた堅牢性を持っています。 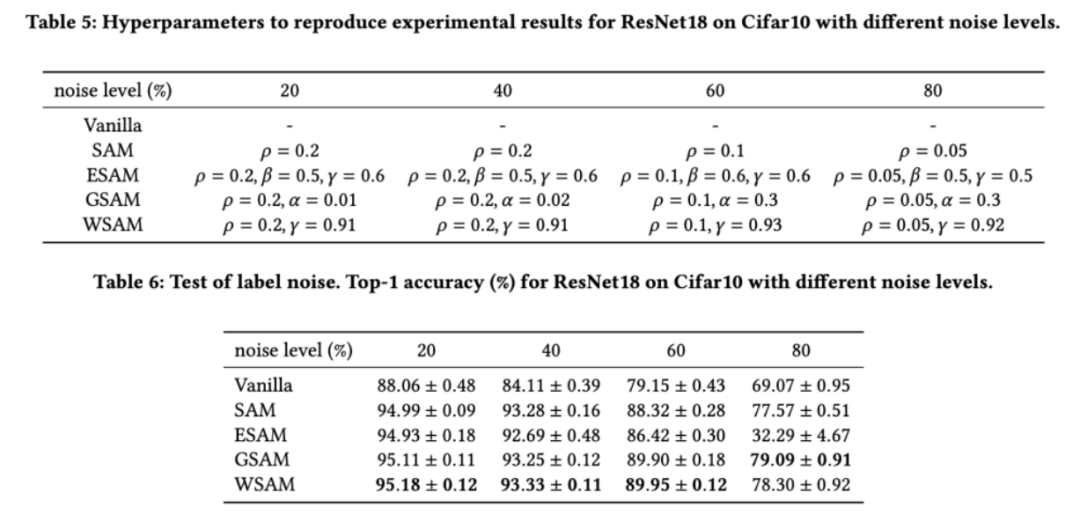
幾何構造の影響の調査
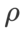 と
と 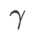 以外のパラメータを除き、画像分類での設定を再利用します。以前の研究 [4、5] によると、ASAM と Fisher SAM の
以外のパラメータを除き、画像分類での設定を再利用します。以前の研究 [4、5] によると、ASAM と Fisher SAM の 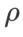 は通常より大きくなります。 {0.1, 0.5, 1.0,…, 6.0} で最適な
は通常より大きくなります。 {0.1, 0.5, 1.0,…, 6.0} で最適な 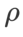 を検索します。ASAM と Fisher SAM の両方で最適な
を検索します。ASAM と Fisher SAM の両方で最適な 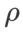 は 5.0 です。その後、ステップ サイズ 0.02 で 0.80 ~ 0.94 の WSAM の最適な
は 5.0 です。その後、ステップ サイズ 0.02 で 0.80 ~ 0.94 の WSAM の最適な 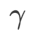 を検索しました。両方の方法の最適な
を検索しました。両方の方法の最適な 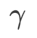 は 0.88 でした。
は 0.88 でした。 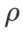 ベースラインを使用して WSAM を直接使用することをお勧めします。
ベースラインを使用して WSAM を直接使用することをお勧めします。 
アブレーション実験
極点分析
ハイパーパラメータの感度
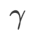 があります。平坦な (急な) 度項のサイズをスケールします。ここでは、このハイパーパラメータに対する WSAM の汎化パフォーマンスの感度をテストします。 Cifar10 および Cifar100 で WSAM を使用し、広範囲の
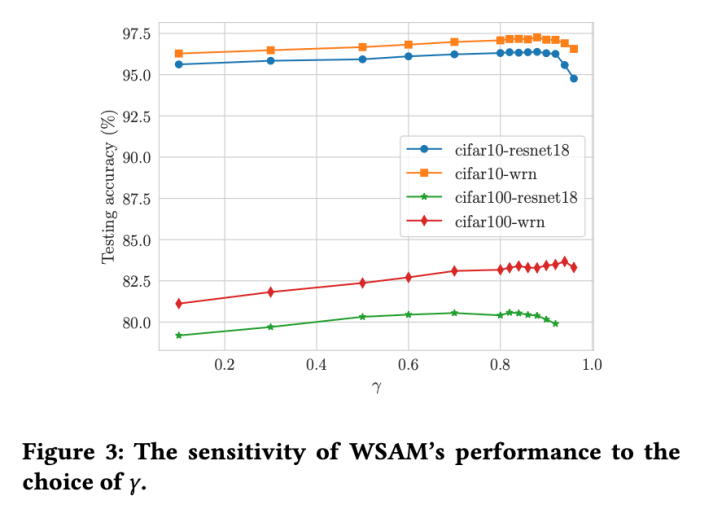
があります。平坦な (急な) 度項のサイズをスケールします。ここでは、このハイパーパラメータに対する WSAM の汎化パフォーマンスの感度をテストします。 Cifar10 および Cifar100 で WSAM を使用し、広範囲の 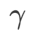 値を使用して ResNet18 および WRN-28-10 モデルをトレーニングしました。図 3 に示すように、結果は、WSAM がハイパーパラメーターの選択に影響を受けないことを示しています。また、WSAM の最適な汎化パフォーマンスは、ほとんどの場合、0.8 ~ 0.95 の間にあることもわかりました。
値を使用して ResNet18 および WRN-28-10 モデルをトレーニングしました。図 3 に示すように、結果は、WSAM がハイパーパラメーターの選択に影響を受けないことを示しています。また、WSAM の最適な汎化パフォーマンスは、ほとんどの場合、0.8 ~ 0.95 の間にあることもわかりました。 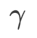
以上がより多用途かつ効果的な、Ant の自社開発オプティマイザー WSAM が KDD Oral に採用されましたの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7484
7484
 15
15
 1377
1377
 52
52
 77
77
 11
11
 19
19
 38
38
 ddrescue を使用して Linux 上のデータを回復する
Mar 20, 2024 pm 01:37 PM
ddrescue を使用して Linux 上のデータを回復する
Mar 20, 2024 pm 01:37 PM
DDREASE は、ハード ドライブ、SSD、RAM ディスク、CD、DVD、USB ストレージ デバイスなどのファイル デバイスまたはブロック デバイスからデータを回復するためのツールです。あるブロック デバイスから別のブロック デバイスにデータをコピーし、破損したデータ ブロックを残して正常なデータ ブロックのみを移動します。 ddreasue は、回復操作中に干渉を必要としないため、完全に自動化された強力な回復ツールです。さらに、ddasue マップ ファイルのおかげでいつでも停止および再開できます。 DDREASE のその他の主要な機能は次のとおりです。 リカバリされたデータは上書きされませんが、反復リカバリの場合にギャップが埋められます。ただし、ツールに明示的に指示されている場合は切り詰めることができます。複数のファイルまたはブロックから単一のファイルにデータを復元します
 オープンソース!ゾーイデプスを超えて! DepthFM: 高速かつ正確な単眼深度推定!
Apr 03, 2024 pm 12:04 PM
オープンソース!ゾーイデプスを超えて! DepthFM: 高速かつ正確な単眼深度推定!
Apr 03, 2024 pm 12:04 PM
0.この記事は何をするのですか?私たちは、多用途かつ高速な最先端の生成単眼深度推定モデルである DepthFM を提案します。従来の深度推定タスクに加えて、DepthFM は深度修復などの下流タスクでも最先端の機能を実証します。 DepthFM は効率的で、いくつかの推論ステップ内で深度マップを合成できます。この作品について一緒に読みましょう〜 1. 論文情報タイトル: DepthFM: FastMonocularDepthEstimationwithFlowMatching 著者: MingGui、JohannesS.Fischer、UlrichPrestel、PingchuanMa、Dmytr
 こんにちは、電気アトラスです!ボストン・ダイナミクスのロボットが復活、180度の奇妙な動きにマスク氏も恐怖
Apr 18, 2024 pm 07:58 PM
こんにちは、電気アトラスです!ボストン・ダイナミクスのロボットが復活、180度の奇妙な動きにマスク氏も恐怖
Apr 18, 2024 pm 07:58 PM
Boston Dynamics Atlas は正式に電動ロボットの時代に突入します!昨日、油圧式アトラスが歴史の舞台から「涙ながらに」撤退したばかりですが、今日、ボストン・ダイナミクスは電動式アトラスが稼働することを発表しました。ボストン・ダイナミクス社は商用人型ロボットの分野でテスラ社と競争する決意を持っているようだ。新しいビデオが公開されてから、わずか 10 時間ですでに 100 万人以上が視聴しました。古い人が去り、新しい役割が現れるのは歴史的な必然です。今年が人型ロボットの爆発的な年であることは間違いありません。ネットユーザーは「ロボットの進歩により、今年の開会式は人間のように見え、人間よりもはるかに自由度が高い。しかし、これは本当にホラー映画ではないのか?」とコメントした。ビデオの冒頭では、アトラスは仰向けに見えるように地面に静かに横たわっています。次に続くのは驚くべきことです
 Google は大喜び: JAX のパフォーマンスが Pytorch や TensorFlow を上回りました! GPU 推論トレーニングの最速の選択肢となる可能性があります
Apr 01, 2024 pm 07:46 PM
Google は大喜び: JAX のパフォーマンスが Pytorch や TensorFlow を上回りました! GPU 推論トレーニングの最速の選択肢となる可能性があります
Apr 01, 2024 pm 07:46 PM
Google が推進する JAX のパフォーマンスは、最近のベンチマーク テストで Pytorch や TensorFlow のパフォーマンスを上回り、7 つの指標で 1 位にランクされました。また、テストは最高の JAX パフォーマンスを備えた TPU では行われませんでした。ただし、開発者の間では、依然として Tensorflow よりも Pytorch の方が人気があります。しかし、将来的には、おそらくより大規模なモデルが JAX プラットフォームに基づいてトレーニングされ、実行されるようになるでしょう。モデル 最近、Keras チームは、ネイティブ PyTorch 実装を使用して 3 つのバックエンド (TensorFlow、JAX、PyTorch) をベンチマークし、TensorFlow を使用して Keras2 をベンチマークしました。まず、主流のセットを選択します
 iPhoneのセルラーデータインターネット速度が遅い:修正
May 03, 2024 pm 09:01 PM
iPhoneのセルラーデータインターネット速度が遅い:修正
May 03, 2024 pm 09:01 PM
iPhone のモバイル データ接続に遅延や遅い問題が発生していませんか?通常、携帯電話の携帯インターネットの強度は、地域、携帯ネットワークの種類、ローミングの種類などのいくつかの要因によって異なります。より高速で信頼性の高いセルラー インターネット接続を実現するためにできることがいくつかあります。解決策 1 – iPhone を強制的に再起動する 場合によっては、デバイスを強制的に再起動すると、携帯電話接続を含む多くの機能がリセットされるだけです。ステップ 1 – 音量を上げるキーを 1 回押して放します。次に、音量小キーを押して、もう一度放します。ステップ 2 – プロセスの次の部分は、右側のボタンを押し続けることです。 iPhone の再起動が完了するまで待ちます。セルラーデータを有効にし、ネットワーク速度を確認します。もう一度確認してください 修正 2 – データ モードを変更する 5G はより優れたネットワーク速度を提供しますが、信号が弱い場合はより適切に機能します
 Kuaishou バージョンの Sora「Ke Ling」がテスト用に公開されています。120 秒以上のビデオを生成し、物理学をより深く理解し、複雑な動きを正確にモデル化できます。
Jun 11, 2024 am 09:51 AM
Kuaishou バージョンの Sora「Ke Ling」がテスト用に公開されています。120 秒以上のビデオを生成し、物理学をより深く理解し、複雑な動きを正確にモデル化できます。
Jun 11, 2024 am 09:51 AM
何?ズートピアは国産AIによって実現するのか?ビデオとともに公開されたのは、「Keling」と呼ばれる新しい大規模な国産ビデオ生成モデルです。 Sora も同様の技術的ルートを使用し、自社開発の技術革新を多数組み合わせて、大きく合理的な動きをするだけでなく、物理世界の特性をシミュレートし、強力な概念的結合能力と想像力を備えたビデオを制作します。データによると、Keling は、最大 1080p の解像度で 30fps で最大 2 分の超長時間ビデオの生成をサポートし、複数のアスペクト比をサポートします。もう 1 つの重要な点は、Keling は研究所が公開したデモやビデオ結果のデモンストレーションではなく、ショートビデオ分野のリーダーである Kuaishou が立ち上げた製品レベルのアプリケーションであるということです。さらに、主な焦点は実用的であり、白紙小切手を書かず、リリースされたらすぐにオンラインに移行することです。Ke Ling の大型モデルは Kuaiying でリリースされました。
 超知性の生命力が覚醒する!しかし、自己更新 AI の登場により、母親はデータのボトルネックを心配する必要がなくなりました。
Apr 29, 2024 pm 06:55 PM
超知性の生命力が覚醒する!しかし、自己更新 AI の登場により、母親はデータのボトルネックを心配する必要がなくなりました。
Apr 29, 2024 pm 06:55 PM
世界は狂ったように大きなモデルを構築していますが、インターネット上のデータだけではまったく不十分です。このトレーニング モデルは「ハンガー ゲーム」のようであり、世界中の AI 研究者は、データを貪欲に食べる人たちにどのように餌を与えるかを心配しています。この問題は、マルチモーダル タスクで特に顕著です。何もできなかった当時、中国人民大学学部のスタートアップチームは、独自の新しいモデルを使用して、中国で初めて「モデル生成データフィード自体」を実現しました。さらに、これは理解側と生成側の 2 つの側面からのアプローチであり、両方の側で高品質のマルチモーダルな新しいデータを生成し、モデル自体にデータのフィードバックを提供できます。モデルとは何ですか? Awaker 1.0 は、中関村フォーラムに登場したばかりの大型マルチモーダル モデルです。チームは誰ですか?ソフォンエンジン。人民大学ヒルハウス人工知能大学院の博士課程学生、ガオ・イージャオ氏によって設立されました。
 アメリカ空軍が初のAI戦闘機を公開し注目を集める!大臣はプロセス全体を通じて干渉することなく個人的にテストを実施し、10万行のコードが21回にわたってテストされました。
May 07, 2024 pm 05:00 PM
アメリカ空軍が初のAI戦闘機を公開し注目を集める!大臣はプロセス全体を通じて干渉することなく個人的にテストを実施し、10万行のコードが21回にわたってテストされました。
May 07, 2024 pm 05:00 PM
最近、軍事界は、米軍戦闘機が AI を使用して完全自動空戦を完了できるようになったというニュースに圧倒されました。そう、つい最近、米軍のAI戦闘機が初めて公開され、その謎が明らかになりました。この戦闘機の正式名称は可変安定性飛行シミュレーター試験機(VISTA)で、アメリカ空軍長官が自ら飛行させ、一対一の空戦をシミュレートした。 5 月 2 日、フランク ケンダル米国空軍長官は X-62AVISTA でエドワーズ空軍基地を離陸しました。1 時間の飛行中、すべての飛行動作が AI によって自律的に完了されたことに注目してください。ケンダル氏は「過去数十年にわたり、私たちは自律型空対空戦闘の無限の可能性について考えてきたが、それは常に手の届かないものだと思われてきた」と語った。しかし今では、




