逆の考え方: MetaMath の新しい数学的推論言語モデルが大規模モデルをトレーニングする
複雑な数的推論は、大規模な言語モデルの推論能力を評価するための重要な指標です。現在、一般的に使用されている数的推論データセットはサンプルサイズが限られており、問題の多様性が不十分であるため、「逆転の呪い」現象が発生しています。大規模な言語モデルでは、つまり、「A は B である」に基づいてトレーニングされた A 言語モデルを「B は A である」に一般化することはできません [1]。数学的推論タスクにおけるこの現象の具体的な形式は次のとおりです。数学的問題が与えられた場合、言語モデルは順推論を使用して問題を解決するのは得意ですが、逆推論で問題を解決する能力に欠けています。次の 2 つの例に示すように、数学の問題では逆推論が非常に一般的です。
1. 典型的な問題 - ニワトリとウサギが同じケージに入っている
- 前向き推論: ケージには 23 羽のニワトリと 12 羽のウサギがいます。檻の中には頭が何本、足は何本あるのか聞いてください。
- 逆の推論: 同じかごの中に数羽のニワトリとウサギがいます。上から数えると頭が 35 本、下から数えると足が 94 本あります。檻の中には鶏とウサギが何羽いますか?
2. GSM8K の質問
- 前向き推論: ジェームズは、それぞれ 4 ポンドの牛肉を 5 パック購入します。牛肉の価格は 1 ポンドあたり 5.50 ドルです。彼はいくら支払いましたか?
- 逆の推論: ジェームズは、1 ポンドあたり 4 ポンドの牛肉を x パック買います。牛肉の価格は 1 ポンドあたり 5.50 ドルです。彼はいくら支払いましたか? 上の質問の答えが 110 であることがわかっている場合、未知の変数 x の値は何ですか?
フォワードサムを改善するには逆推論機能を実現するために、ケンブリッジ、香港科技大学、およびファーウェイの研究者は、一般的に使用される 2 つの数学的データ セット (GSM8K および MATH) に基づいた MetaMathQA データ セットを提案しました。高品質。 MetaMathQA は、大規模な言語モデルによって生成された 395K の順方向および逆方向の数学的な質問と回答のペアで構成されています。彼らは、MetaMathQA データ セットで LLaMA-2 を微調整して、数学的推論 (順方向および逆数) に焦点を当てた大規模な言語モデルである MetaMath を取得しました。これは、数学的推論データ セットで SOTA に到達しました。さまざまなスケールの MetaMathQA データセットと MetaMath モデルは、研究者による使用のためにオープンソース化されています。

- プロジェクトアドレス: https://meta-math.github.io/ 論文アドレス: https://arxiv.org/abs/2309.12284
- データ アドレス: https://huggingface.co/datasets/meta-math/MetaMathQA
- モデルアドレス: https://huggingface.co/meta-math
- コードアドレス: https://github.com/meta-math/MetaMath
#MetaMathQA には 4 つのデータ拡張メソッドが含まれています:
1. 回答拡張 (回答拡張):
問題が与えられた場合、正しい結果を得ることができる思考の連鎖が、データ拡張として大規模な言語モデルを通じて生成されます。 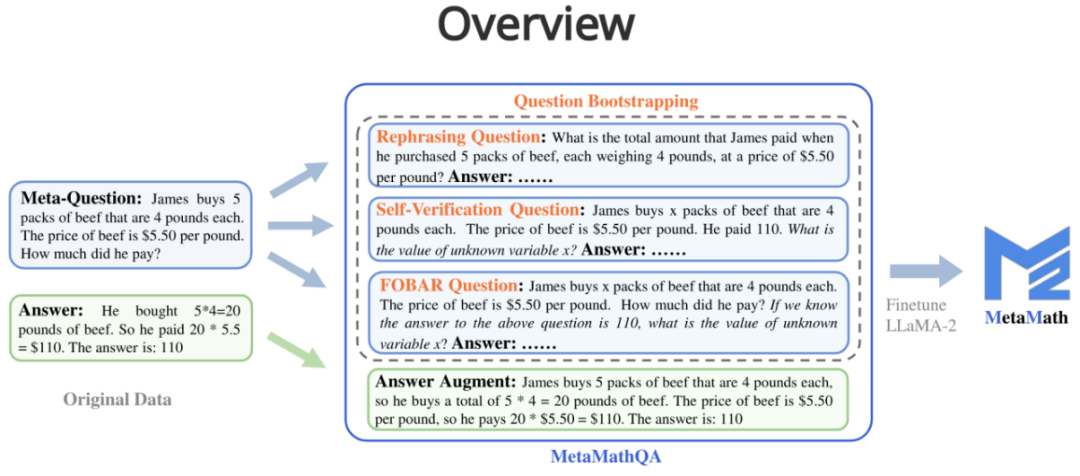
質問: ジェームズは、それぞれ 4 ポンドの牛肉を 5 パック購入します。牛肉の価格は 1 ポンドあたり 5.50 ドルです。彼はいくら支払いましたか?
答え: ジェームズは、それぞれ 4 ポンドの牛肉を 5 パック購入するので、合計 5 * 4 = 20 ポンドの牛肉を購入します。牛肉の価格は 1 ポンドあたり 5.50 ドルなので、彼は 20 * 5.50 ドルを支払います= $110。答えは: 110.2. 質問の言い換え (質問書き換えの強化):
- 指定されたメタ質問、大規模な言語モデルを通じて問題を書き換え、データ拡張として正しい結果が得られる思考連鎖を生成します。
- #質問: ジェームズが 1 ポンドあたり 5.50 ドルの重さ 4 ポンドの牛肉を 5 パック購入したときに支払った総額はいくらですか?
- 答え: 牛肉の各パックの重さは 4 ポンドなので、5 パックの重さは合計 4 * 5 = 20 ポンドです。牛肉 1 ポンドあたりの価格は 5.50 ドルなので、20 ポンドの合計コストは 20 * 5.50 ドル = 110 ドルとなります。したがって、 James は合計 $110 を支払いました。答えは 110.
##3. FOBAR 質問 (FOBAR 逆質問拡張): #メタ質問が与えられた場合、マスク条件の数値は次のようになります。例:「上の質問に対する答えが 110 であることがわかっている場合、未知の変数 x の値は何ですか?」)。
- 質問: ジェームズは、それぞれ 4 ポンドの牛肉を x パック購入します。牛肉の価格は 1 ポンドあたり 5.50 ドルです。彼はいくら支払いましたか? の答えがわかっている場合上の質問は 110 です。未知の変数 x の値は何ですか?
- 答え: ジェームズはそれぞれ 4 ポンドの牛肉を x パック購入するため、合計 4 ポンドの牛肉を購入します。牛肉。牛肉の価格は 1 ポンドあたり 5.50 ドルなので、牛肉の総コストは 5.50 * 4x = 22x です。総コストは 110 ドルと与えられているので、次のように書くことができます: 22x = 110。両辺を 22 で割ると、 x = 5 が得られます。x の値は 5 です。
4. 自己確認の質問 (自己確認の逆質問の拡張): FOBAR に基づいて、逆問題部分を大規模な言語モデルを使用したステートメントに書き換えることによってデータ拡張が実行されます (書き換え例:「彼はいくら払いましたか?」(答えは 110) は「彼はいくら払いましたか?」に書き換えられました) 110インチを支払いました)。
- 質問: ジェームズは、それぞれ 4 ポンドの牛肉を x パック購入します。牛肉の価格は 1 ポンドあたり 5.50 ドルです。彼は 110 支払いました。未知の変数 x の値は何ですか? ?
- 答え: この問題を解決するには、ジェームズが買った牛肉のパックの数を表す x の値を決定する必要があります。牛肉の各パックの重さは 4 ポンドで、コストは1 ポンドあたり 5.50 ドル。ジェームスが支払った合計金額は 110 ドルです。次のように方程式を設定できます: 牛肉のパック数 * パックあたりの重量 * ポンドあたりの価格 = 支払総額; x * 4 * $5.50 = $110; 単純化してみましょう。 x を解く: 4x * $5.50 = $110; 22x = $110; x を分離するには、方程式の両辺を 22 で割ります: 22x / 22 = $110 / 22; x = $5; x の値は 5.

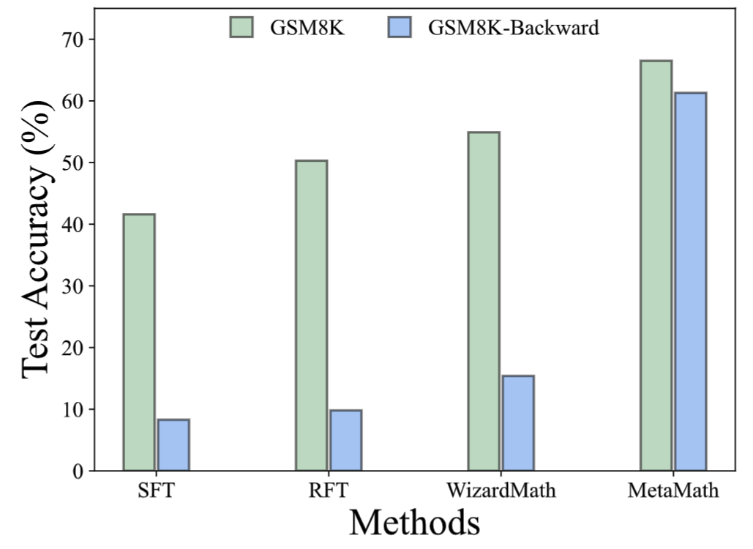
 ##2 つの一般的な数学における実験結果推論データ セット (GSM8K および MATH) は、MetaMath が既存のオープンソース LLM モデルよりもパフォーマンスが大幅に優れており、外部ツール (コード インタプリタなど) の使用を必要としないことを示しています。その中で、当社の MetaMath-7B モデルは、GSM8K で 66.5%、MATH で 19.8% の精度に達しており、同じスケールの最先端のモデルよりもそれぞれ 11.6% と 9.1% 高い精度を示しています。特に言及する価値があるのは、MetaMath-70B が GSM8K 上で GPT-3.5-Turbo を上回る 82.3% の精度を達成したことです。
##2 つの一般的な数学における実験結果推論データ セット (GSM8K および MATH) は、MetaMath が既存のオープンソース LLM モデルよりもパフォーマンスが大幅に優れており、外部ツール (コード インタプリタなど) の使用を必要としないことを示しています。その中で、当社の MetaMath-7B モデルは、GSM8K で 66.5%、MATH で 19.8% の精度に達しており、同じスケールの最先端のモデルよりもそれぞれ 11.6% と 9.1% 高い精度を示しています。特に言及する価値があるのは、MetaMath-70B が GSM8K 上で GPT-3.5-Turbo を上回る 82.3% の精度を達成したことです。「表面配置の仮定」[2] によると、大規模な言語モデルの多くは事前トレーニングから得られ、下流のタスクからのデータは事前トレーニング中に学習された言語モデルの固有の機能を活性化します。したがって、これは 2 つの重要な疑問を引き起こします: (i) どのタイプのデータが潜在知識を最も効果的に活性化するのか、(ii) なぜあるデータセットが他のデータセットよりもそのような活性化に優れているのか?
MetaMathQA が役立つのはなぜですか?思考連鎖データ (Perplexity) の品質の向上
 #上図に示すように、研究者は Perplexity を計算しました。回答のみのデータ、GSM8K CoT、および MetaMathQA データセットのさまざまな部分に関する LLaMA-2-7B モデルの分析。 MetaMathQA データセットの混乱度は他の 2 つのデータセットよりも大幅に低く、これは学習可能性が高く、モデルの潜在的な知識を明らかにするのにより役立つ可能性があることを示しています
#上図に示すように、研究者は Perplexity を計算しました。回答のみのデータ、GSM8K CoT、および MetaMathQA データセットのさまざまな部分に関する LLaMA-2-7B モデルの分析。 MetaMathQA データセットの混乱度は他の 2 つのデータセットよりも大幅に低く、これは学習可能性が高く、モデルの潜在的な知識を明らかにするのにより役立つ可能性があることを示していますMetaMathQA が役立つのはなぜですか?思考連鎖データの多様性を高める (Diversity)

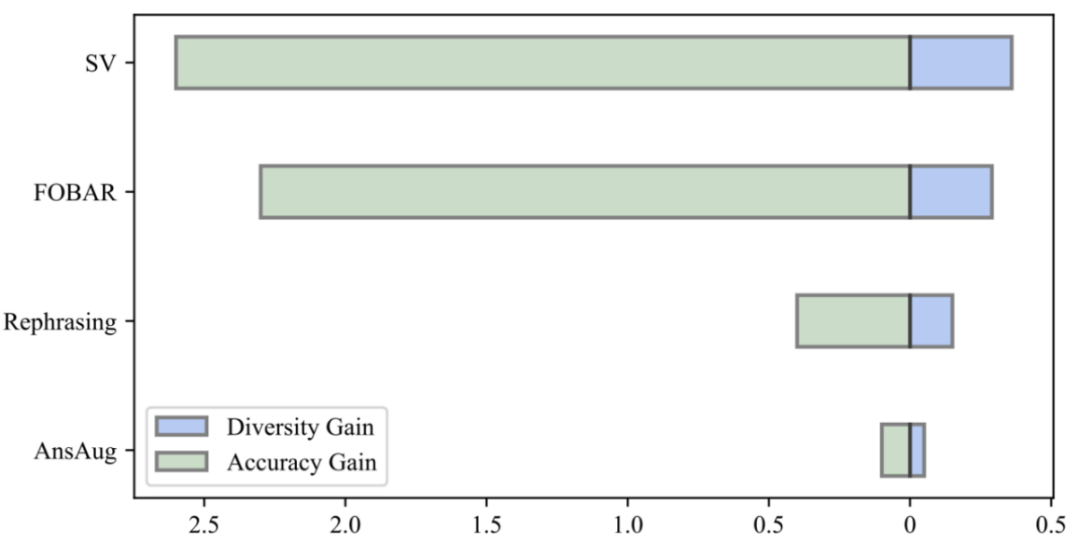
研究者らは、データの多様性の向上とモデルの精度の向上を比較することで、再定式化、FOBAR、SV による同量の拡張データの導入が有効であることを発見しました。大幅な多様性の向上が達成され、モデルの精度が大幅に向上しました。対照的に、回答拡張のみを使用すると、精度が大幅に飽和してしまいました。精度が飽和に達すると、AnsAug データを追加しても限られたパフォーマンスの向上しか得られません
以上が逆の考え方: MetaMath の新しい数学的推論言語モデルが大規模モデルをトレーニングするの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7733
7733
 15
15
 1643
1643
 14
14
 1397
1397
 52
52
 1290
1290
 25
25
 1233
1233
 29
29
 WorldCoin(WLD)価格予測2025-2031:WLDは2031年までに4ドルに達しますか?
Apr 21, 2025 pm 02:42 PM
WorldCoin(WLD)価格予測2025-2031:WLDは2031年までに4ドルに達しますか?
Apr 21, 2025 pm 02:42 PM
WorldCoin(WLD)は、独自の生体認証とプライバシー保護メカニズムを備えた暗号通貨市場で際立っており、多くの投資家の注目を集めています。 WLDは、特にOpenai人工知能技術と組み合わせて、革新的なテクノロジーを備えたAltcoinsの間で驚くほど演奏しています。しかし、デジタル資産は今後数年間でどのように振る舞いますか? WLDの将来の価格を一緒に予測しましょう。 2025年のWLD価格予測は、2025年にWLDで大幅に増加すると予想されています。市場分析は、平均WLD価格が1.31ドルに達する可能性があり、最大1.36ドルであることを示しています。ただし、クマ市場では、価格は約0.55ドルに低下する可能性があります。この成長の期待は、主にWorldCoin2によるものです。
 クロスチェーントランザクションとはどういう意味ですか?クロスチェーントランザクションとは何ですか?
Apr 21, 2025 pm 11:39 PM
クロスチェーントランザクションとはどういう意味ですか?クロスチェーントランザクションとは何ですか?
Apr 21, 2025 pm 11:39 PM
クロスチェーントランザクションをサポートする交換:1。Binance、2。Uniswap、3。Sushiswap、4。CurveFinance、5。Thorchain、6。1inchExchange、7。DLNTrade、これらのプラットフォームはさまざまな技術を通じてマルチチェーン資産トランザクションをサポートします。
 なぜ仮想通貨価格の上昇または下落があるのですか?なぜ仮想通貨価格の上昇または下落があるのですか?
Apr 21, 2025 am 08:57 AM
なぜ仮想通貨価格の上昇または下落があるのですか?なぜ仮想通貨価格の上昇または下落があるのですか?
Apr 21, 2025 am 08:57 AM
仮想通貨価格の上昇の要因には、次のものが含まれます。1。市場需要の増加、2。供給の減少、3。刺激された肯定的なニュース、4。楽観的な市場感情、5。マクロ経済環境。衰退要因は次のとおりです。1。市場需要の減少、2。供給の増加、3。ネガティブニュースのストライキ、4。悲観的市場感情、5。マクロ経済環境。
 Aavenomicsは、Aaveプロトコルトークンを変更し、Tokenの買戻しを導入するための推奨事項です。
Apr 21, 2025 pm 06:24 PM
Aavenomicsは、Aaveプロトコルトークンを変更し、Tokenの買戻しを導入するための推奨事項です。
Apr 21, 2025 pm 06:24 PM
Aavenomicsは、Aaveプロトコルトークンを変更し、Aavedaoの定足数を実装したToken Reposを導入する提案です。 Aave Project Chain(ACI)の創設者であるMarc Zellerは、これをXで発表し、契約の新しい時代をマークしていることに注目しました。 Aave Chain Initiative(ACI)の創設者であるMarc Zellerは、Aavenomicsの提案にAave Protocolトークンの変更とトークンリポジトリの導入が含まれていると発表しました。 Zellerによると、これは契約の新しい時代を告げています。 Aavedaoのメンバーは、水曜日の週に100でした。
 カーネルエアドロップ報酬を獲得する方法バイナンスフルプロセス戦略
Apr 21, 2025 pm 01:03 PM
カーネルエアドロップ報酬を獲得する方法バイナンスフルプロセス戦略
Apr 21, 2025 pm 01:03 PM
暗号通貨の賑やかな世界では、新しい機会が常に現れます。現在、Kerneldao(Kernel)Airdropアクティビティは多くの注目を集め、多くの投資家の注目を集めています。それで、このプロジェクトの起源は何ですか? BNBホルダーはそれからどのような利点を得ることができますか?心配しないでください、以下はあなたのためにそれを一つ一つ明らかにします。
 ハイブリッドブロックチェーン取引プラットフォームとは何ですか?
Apr 21, 2025 pm 11:36 PM
ハイブリッドブロックチェーン取引プラットフォームとは何ですか?
Apr 21, 2025 pm 11:36 PM
暗号通貨交換を選択するための提案:1。流動性の要件については、優先度は、その順序の深さと強力なボラティリティ抵抗のため、Binance、gate.ioまたはokxです。 2。コンプライアンスとセキュリティ、Coinbase、Kraken、Geminiには厳格な規制の承認があります。 3.革新的な機能、Kucoinのソフトステーキング、Bybitのデリバティブデザインは、上級ユーザーに適しています。
 通貨サークル市場に関するリアルタイムデータの上位10の無料プラットフォーム推奨事項がリリースされます
Apr 22, 2025 am 08:12 AM
通貨サークル市場に関するリアルタイムデータの上位10の無料プラットフォーム推奨事項がリリースされます
Apr 22, 2025 am 08:12 AM
初心者に適した暗号通貨データプラットフォームには、Coinmarketcapと非小さいトランペットが含まれます。 1。CoinMarketCapは、初心者と基本的な分析のニーズに合わせて、グローバルなリアルタイム価格、市場価値、取引量のランキングを提供します。 2。小さい引用は、中国のユーザーが低リスクの潜在的なプロジェクトをすばやくスクリーニングするのに適した中国フレンドリーなインターフェイスを提供します。
 Rexas Finance(RXS)は、2025年にSolana(Sol)、Cardano(ADA)、XRP、Dogecoin(Doge)を上回ることができます
Apr 21, 2025 pm 02:30 PM
Rexas Finance(RXS)は、2025年にSolana(Sol)、Cardano(ADA)、XRP、Dogecoin(Doge)を上回ることができます
Apr 21, 2025 pm 02:30 PM
不安定な暗号通貨市場では、投資家は人気のある通貨を超えた代替品を探しています。 Solana(Sol)、Cardano(ADA)、XRP、Dogecoin(DOGE)などのよく知られた暗号通貨も、市場の感情、規制の不確実性、スケーラビリティなどの課題に直面しています。ただし、新しい新興プロジェクトであるRexasFinance(RXS)が出現しています。それは有名人の効果や誇大広告に依存するのではなく、現実世界の資産(RWA)とブロックチェーン技術を組み合わせて投資家に革新的な投資方法を提供することに焦点を当てています。この戦略により、2025年の最も成功したプロジェクトの1つになることを望んでいます。Rexasfi




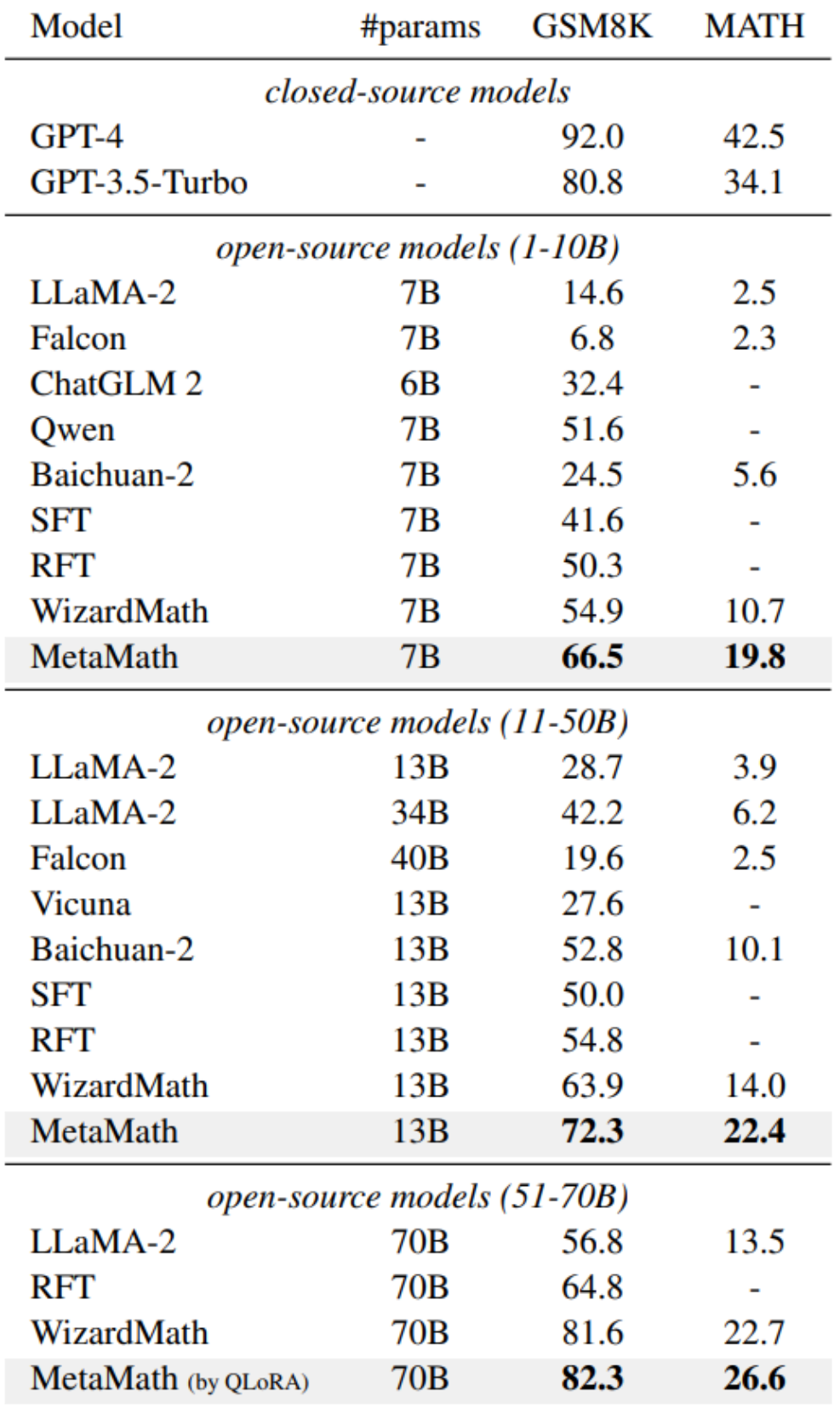
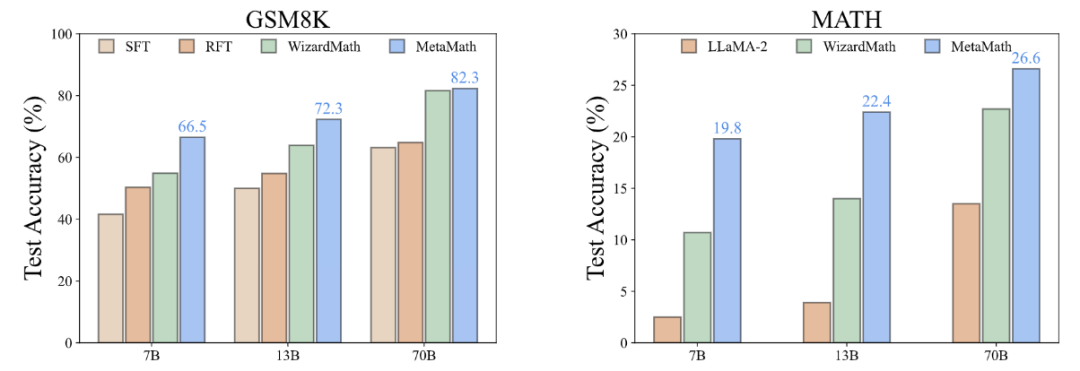 ##2 つの一般的な数学における実験結果推論データ セット (GSM8K および MATH) は、MetaMath が既存のオープンソース LLM モデルよりもパフォーマンスが大幅に優れており、外部ツール (コード インタプリタなど) の使用を必要としないことを示しています。その中で、当社の MetaMath-7B モデルは、GSM8K で 66.5%、MATH で 19.8% の精度に達しており、同じスケールの最先端のモデルよりもそれぞれ 11.6% と 9.1% 高い精度を示しています。特に言及する価値があるのは、MetaMath-70B が GSM8K 上で GPT-3.5-Turbo を上回る 82.3% の精度を達成したことです。
##2 つの一般的な数学における実験結果推論データ セット (GSM8K および MATH) は、MetaMath が既存のオープンソース LLM モデルよりもパフォーマンスが大幅に優れており、外部ツール (コード インタプリタなど) の使用を必要としないことを示しています。その中で、当社の MetaMath-7B モデルは、GSM8K で 66.5%、MATH で 19.8% の精度に達しており、同じスケールの最先端のモデルよりもそれぞれ 11.6% と 9.1% 高い精度を示しています。特に言及する価値があるのは、MetaMath-70B が GSM8K 上で GPT-3.5-Turbo を上回る 82.3% の精度を達成したことです。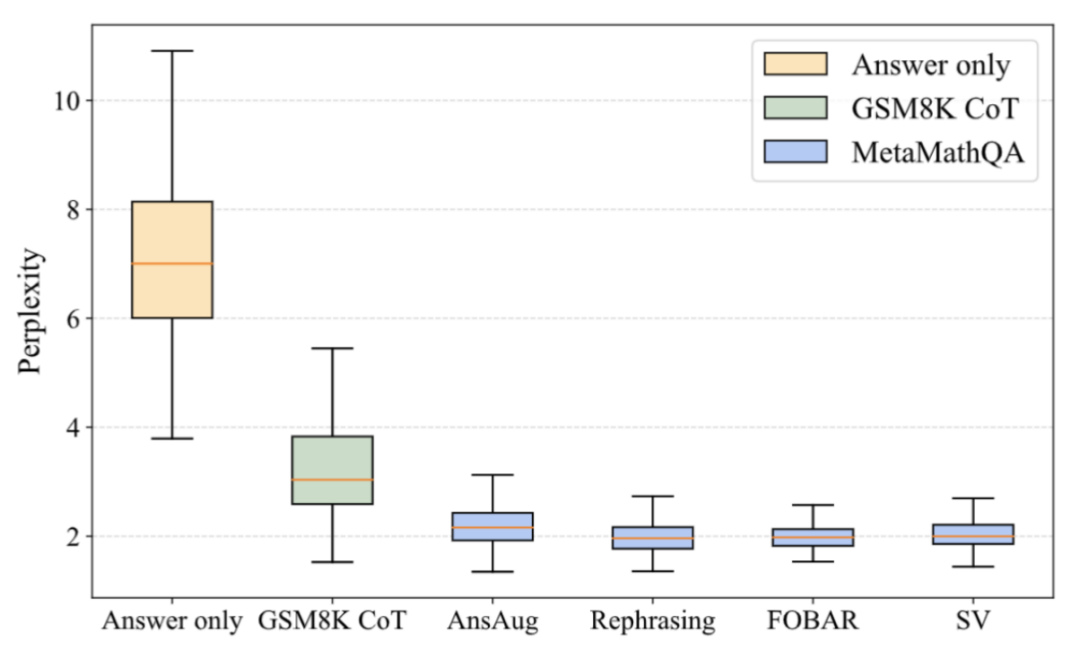 #上図に示すように、研究者は Perplexity を計算しました。回答のみのデータ、GSM8K CoT、および MetaMathQA データセットのさまざまな部分に関する LLaMA-2-7B モデルの分析。 MetaMathQA データセットの混乱度は他の 2 つのデータセットよりも大幅に低く、これは学習可能性が高く、モデルの潜在的な知識を明らかにするのにより役立つ可能性があることを示しています
#上図に示すように、研究者は Perplexity を計算しました。回答のみのデータ、GSM8K CoT、および MetaMathQA データセットのさまざまな部分に関する LLaMA-2-7B モデルの分析。 MetaMathQA データセットの混乱度は他の 2 つのデータセットよりも大幅に低く、これは学習可能性が高く、モデルの潜在的な知識を明らかにするのにより役立つ可能性があることを示しています