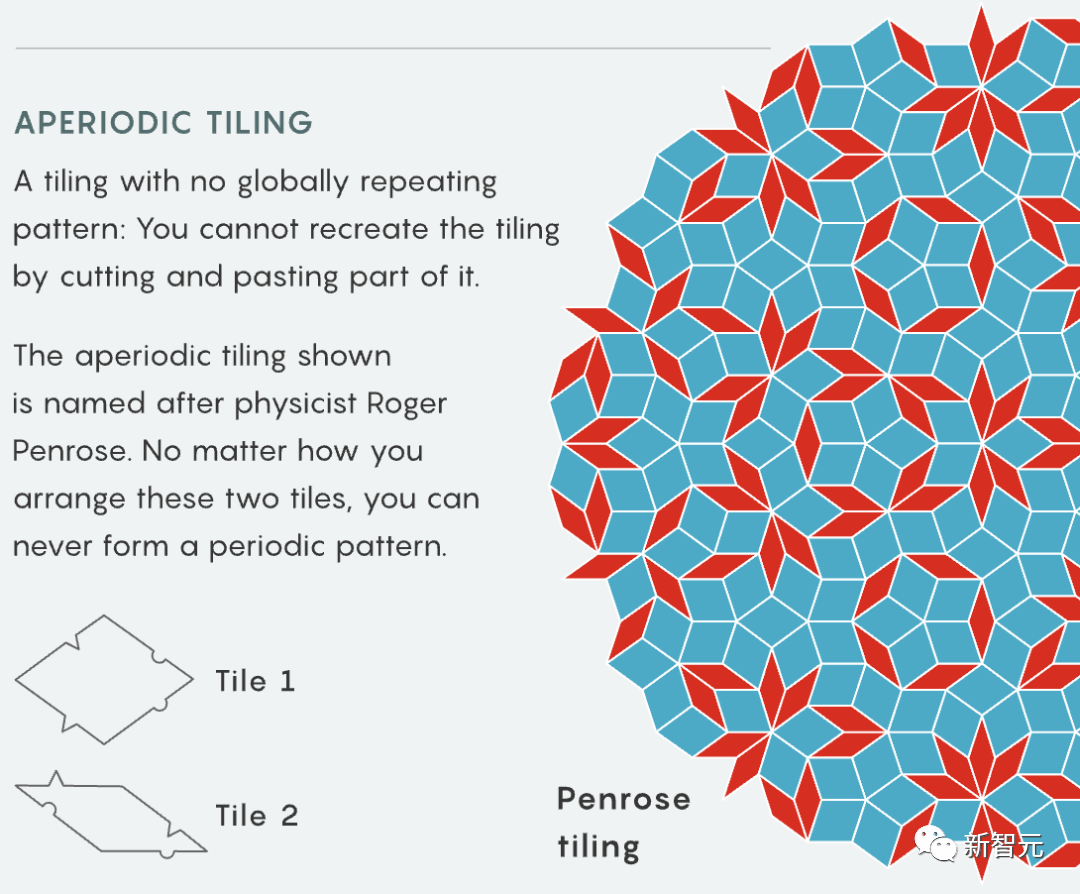
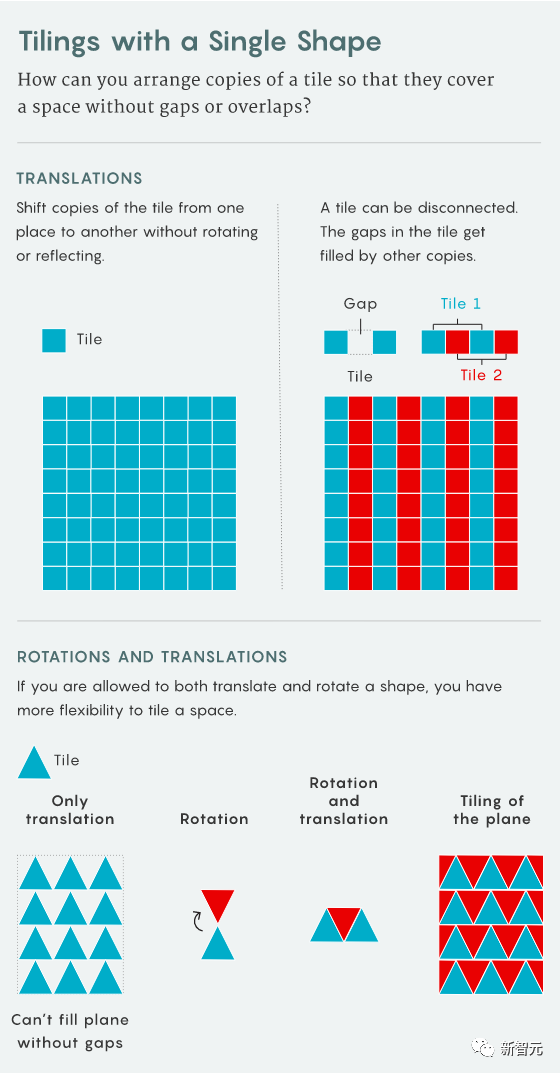
テレンス・タオが、60 年来の幾何学の新たな問題にアプローチします。定期的な閉鎖舗装の問題に新たなブレークスルーがもたらされました
Tao Zhexuan は、周期的密舗装問題の研究において新たな進歩を遂げました。
9 月 18 日、Tao Zhexuan と Rachel Greenfeld は、プレプリントされた論文「Translational Single Mingling Pavement」を発表しました。 「並進モノタイリングの決定不可能性」をarXivにアップロードしました。

論文アドレス: https://arxiv.org/abs/2309.09504
この論文主な結論は、グリッドの次元が制限されていない場合、グリッドの有限サブセットがグリッドの周期サブセットをタイル化できるかどうかを決定する問題は決定できないということです。
次のことに注意してください。この問題は次元 1 と次元 2 で決定可能です。
#Tao Zhexuan 氏は、この記事で紹介されているコンポーネントのほとんどが人気のあるゲームに似ているのは少し奇妙だと述べています—
ドミノ、数独、コンピュータ ゲーム「テトリス」、さらには子供向けゲーム「フィズ バズ」にさえ似たものがたくさんあります。
なぜ勉強するのか、なぜ勉強するのか数学の問題にはそんなにたくさんのゲームが含まれているのですか?テレンス・タオも説明できません

並進単一密タイリングの決定不可能性
この論文は、二人の以前の論文の続編。リンク周期タイル問題
前回の論文では、高次元グリッドを構築しました 単一の密な舗装
単一の密な舗装 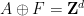
(したがって、単一の密な舗装 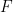 は有限集合です)。これは非周期的です。 (このタイルを周期タイル
は有限集合です)。これは非周期的です。 (このタイルを周期タイル 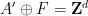 に「修正」する方法はありません。
に「修正」する方法はありません。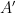 は有限インデックス サブグループ # を基準としています。 ## は定期的です)。
は有限インデックス サブグループ # を基準としています。 ## は定期的です)。 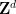

##(「ハット単密舗装」は、最近発見された非周期的等距離単密舗装です。
。この種の単密舗装では、回転の使用が許可されています。 、反射と変換、または新しい「ゴースト モノリス」。これらのモノリスは、反射が必要ないことを除いて、ハット モノリスに似ています)。 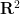 テレンス タオとレイチェル グリーンフェルドがこの予想を引き起こした理由の 1 つは、数学者ハオ ワンの観察です。
テレンス タオとレイチェル グリーンフェルドがこの予想を引き起こした理由の 1 つは、数学者ハオ ワンの観察です。
彼は、周期的テッセレーション予想が正しい場合、並進テッセレーション問題はアルゴリズムによって決定可能であることを発見しました—
次元 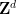 と有限部分集合
と有限部分集合 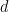 が与えられたとき、
が与えられたとき、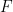 のチューリング マシンがあります。今回は、
のチューリング マシンがあります。今回は、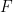 # を高密度に舗装できるかどうかを限られた時間内で判断できます。
# を高密度に舗装できるかどうかを限られた時間内で判断できます。 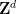 これは、周期的なタイリングがある場合は、コンピューター検索で見つけることができるためです。
これは、周期的なタイリングがある場合は、コンピューター検索で見つけることができるためです。
タイリングがまったくない場合は、次に、コンパクト性定理から、
素翻訳ではカバーできない限定された 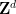 サブセットがいくつかあることがわかります。これは、コンピューター検索でも行うことができます。発見する。
サブセットがいくつかあることがわかります。これは、コンピューター検索でも行うことができます。発見する。 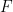 周期的テッセレーション予想は、考えられる状況はこれら 2 つだけであると主張し、決定可能性を与えます。
周期的テッセレーション予想は、考えられる状況はこれら 2 つだけであると主張し、決定可能性を与えます。
 一方、Wang の視点は不変です。周期的テッセレーション予想の失敗は、自動的に並進テッセレーション予想の失敗を意味するわけではありません。周期的タイリングの存在に依存しないタイリングを決定する他のアルゴリズムの存在を排除しないため、問題の決定不可能性
一方、Wang の視点は不変です。周期的テッセレーション予想の失敗は、自動的に並進テッセレーション予想の失敗を意味するわけではありません。周期的タイリングの存在に依存しないタイリングを決定する他のアルゴリズムの存在を排除しないため、問題の決定不可能性
(例: 新しく発見されたアルゴリズムを使用した場合でも)ハットとゴースト タイリングと同様に、
の有理係数を持つポリゴンの等角単一タイリング問題が、反射があるかどうかにかかわらず、決定可能であるかどうかはまだ未解決の問題です。 #この記事の主な結果は、この問題に対処しています (警告あり): 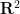
書き直す必要があるのは次のとおりです。定理 1

には、次元 、周期サブセットが与えられた場合、
にはアルゴリズムが存在しません。 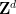 、および有限サブセット
、および有限サブセット 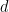 。限られた時間内に並進タイルがあるかどうかを判断できます
。限られた時間内に並進タイルがあるかどうかを判断できます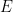 ##.
##. 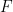
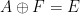
すべての 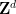 の代わりに
の代わりに 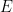 の周期的なサブセット
の周期的なサブセット 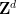 を使用する必要があることに注意してください。これは主にこのアプローチの技術的な制限によるものであり、追加の努力と創造性によって除去できる可能性があります。
を使用する必要があることに注意してください。これは主にこのアプローチの技術的な制限によるものであり、追加の努力と創造性によって除去できる可能性があります。
#さらに、テレンス タオとレイチェル グリーンフェルドは、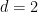 のとき、周期舗装予想がバタチャリヤによって確立されたことに気づきました。 #この場合、問題は特定できます。
のとき、周期舗装予想がバタチャリヤによって確立されたことに気づきました。 #この場合、問題は特定できます。 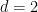
の固定値については、タイリングの問題が決定可能であるかどうかはまだ不明です (上記の結果では、寸法 が使用されていることに注意してください) 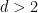 は固定ではなく、入力の一部です)。
は固定ではなく、入力の一部です)。 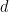
 この定理はまた、アルゴリズム上の決定不能性と論理的決定不能性 (論理的独立性とも呼ばれます) の間のよく知られた関係により、次のことがわかります。次元
この定理はまた、アルゴリズム上の決定不能性と論理的決定不能性 (論理的独立性とも呼ばれます) の間のよく知られた関係により、次のことがわかります。次元
、
 、# の (原理的に明確に記述可能な) 周期的なサブセットが存在します。 有限のサブセット
、# の (原理的に明確に記述可能な) 周期的なサブセットが存在します。 有限のサブセット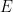 の
の 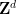 ##、したがって
##、したがって 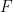 は並進タイリングを通過できます
は並進タイリングを通過できます 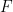 は ZFC 集合論では使用できません 確認あるいは改ざんする(もちろん理論が一貫していると仮定して)。
は ZFC 集合論では使用できません 確認あるいは改ざんする(もちろん理論が一貫していると仮定して)。 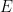 #このアプローチの結果、## の代わりに「ほぼ 2 次元」グループ
#このアプローチの結果、## の代わりに「ほぼ 2 次元」グループ
を使用することもできます。ここで #、 は有限アーベル群です (次元
は有限アーベル群です (次元 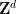 の代わりに入力の一部になります)。
の代わりに入力の一部になります)。 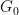 次に、証明の主なアイデアをいくつか説明します。
次に、証明の主なアイデアをいくつか説明します。 
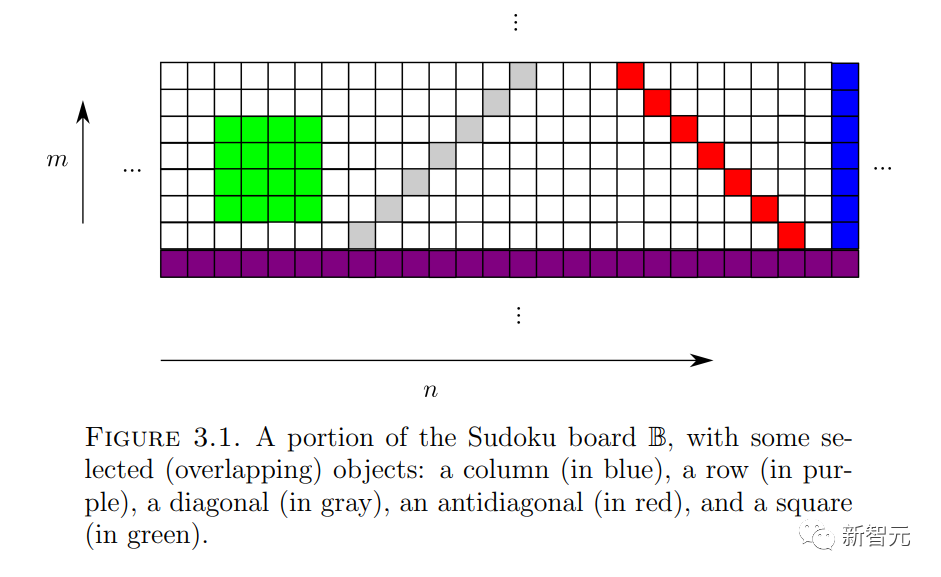
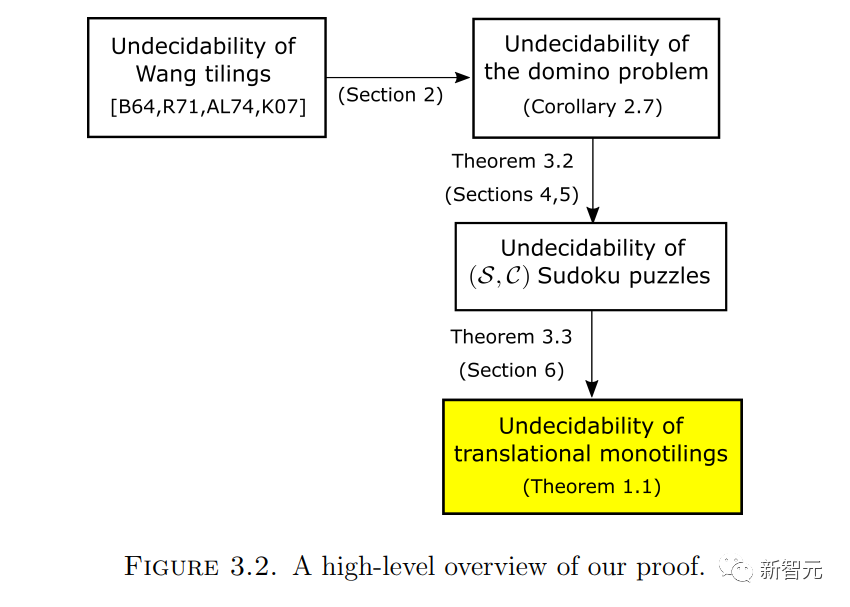
したがって、Wang の密舗装問題を 1 つの密舗装問題としてエンコードします。 ##2 番目の質問は、Wang の秘密ショップの問題に関するものです。 Wang の秘密ショップ セットが限定されているとします。 バーガーがかつてこの問題を決定することはできないと結論付けたことは有名です。 書き直す必要がある内容は次のとおりです: Berger、Robert、 この問題を高次元の並進単一密タイリング問題に変換するには、いくつかの中間問題を解決する必要があります まず、Wang の秘密ショップ問題を、ドミノ問題と呼ばれる同様の問題に簡単に埋め込むことができます。 次のように書き換えられます: ドミノ問題は問題 3です。 ドミノのレベル (または垂直) 有限セットが与えられた場合 、 は、水平または垂直に隣接し、同じエッジ色を持つ Wang の密なタイルのペアです。 #質問 4 (数独の問題) 指定された列幅 数独問題を単一の密な舗装問題に埋め込むことは、以前の論文で提案された修正方法に基づいています これらの論文でも提案されています異なるバージョン数独の問題を解析し、さまざまな問題 (数独の問題を含む) を 1 つのタイル問題に変換できる「タブ言語」と呼ばれるメソッドを作成しました。 ドミノ問題を数独の問題としてエンコードするには、ドミノ関数 (特定のドミノ セット 関連するドミノ制約と同じルールに従います) を取得し、それを使用して構築する必要があります。 Sudoku 関数 このアプローチはすぐにはわかりませんが、タオとレイチェル・グリーンフェルドはエマニュエル・ジャンデルの助けを借りてアデラーとルイスのアイデアの一部を採用し、特定の階層を使用して 1 つの質問をエンコードしました別のものに。 ここでは、階層構造 次に、式 は 2 つの異なる大きな素数です (たとえば、 の 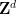 :
: 
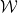 (単位 (平方、各エッジには限られたパレットから特定の色が割り当てられています)、隣接するタイルがエッジに同じ色を共有するように、標準グリッド
(単位 (平方、各エッジには限られたパレットから特定の色が割り当てられています)、隣接するタイルがエッジに同じ色を共有するように、標準グリッド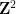 を使用して変換によって平面をテッセレーションすることは可能ですか?
を使用して変換によって平面をテッセレーションすることは可能ですか? 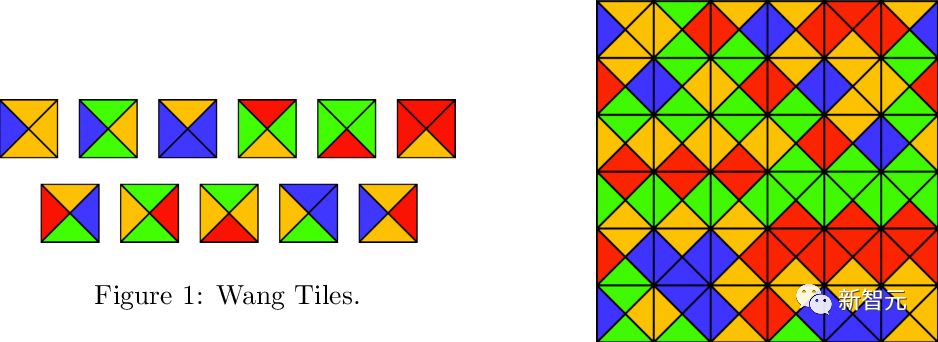


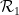 または
または 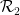 は隣接する単位正方形のペアであり、各単位正方形は有限集合 ## で表されます。 # の要素点で装飾するには
は隣接する単位正方形のペアであり、各単位正方形は有限集合 ## で表されます。 # の要素点で装飾するには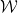 、標準格子タイリング
、標準格子タイリング 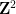 の各単位正方形に点を割り当てて、このタイリングの各ペアが水平 (または垂直) 正方形で のドミノを使用できるようにすることはできますか? ###### または #########?
の各単位正方形に点を割り当てて、このタイリングの各ペアが水平 (または垂直) 正方形で のドミノを使用できるようにすることはできますか? ###### または #########? 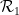
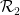 #実際には、各 Wang のタイルを個別の「ポイント」として挿入し、ドミノ セットを定義するだけです
#実際には、各 Wang のタイルを個別の「ポイント」として挿入し、ドミノ セットを定義するだけです
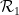 次のステップでは、ドミノの問題と数独の問題を組み合わせます:
次のステップでは、ドミノの問題と数独の問題を組み合わせます: 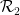

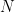 、数値のセット
、数値のセット 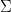 、関数のセット
、関数のセット 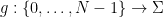
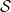 、および「初期条件」
、および「初期条件」 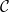 (ここでは詳しく説明しませんが)、「数独ボード」の
(ここでは詳しく説明しませんが)、「数独ボード」の 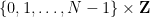 # の各セルに番号を割り当てることはできますか?
# の各セルに番号を割り当てることはできますか? 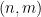 # # 任意の傾き
# # 任意の傾き 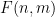 と切片
と切片 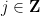 について、
について、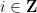 # 線 ## に沿った数値 # となります。は
# 線 ## に沿った数値 # となります。は 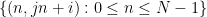 にあります (そして
にあります (そして 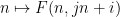 は初期条件
は初期条件  の対象となります)?
の対象となります)? 
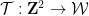 (ドミノ セットに関連付けられたいくつかの Sudoku 制約に従います); 逆に、それぞれは Sudoku パズルのルールに従います。 Sudoku 関数は、何らかの方法でドミノ関数から生成される必要があります。
(ドミノ セットに関連付けられたいくつかの Sudoku 制約に従います); 逆に、それぞれは Sudoku パズルのルールに従います。 Sudoku 関数は、何らかの方法でドミノ関数から生成される必要があります。 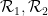
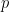 について説明します (ドミノ問題の 2 次元の性質により、2 つの異なる素数を使用する必要があります)。
について説明します (ドミノ問題の 2 次元の性質により、2 つの異なる素数を使用する必要があります)。 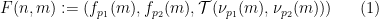 を使用して数独関数
を使用して数独関数 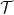 を作成します。これには何らかの埋め込みが行われます。
を作成します。これには何らかの埋め込みが行われます。 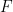 # ここで、
# ここで、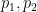 、## を使用できます) #)、
、## を使用できます) #)、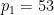 は
は 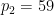 を
を 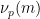 で割った回数を表し、
で割った回数を表し、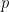
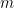 は、
は、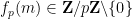 展開の最後のゼロ以外の数字です:
展開の最後のゼロ以外の数字です: 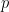
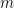 ##### ##########(#########、そして#########)。
##### ##########(#########、そして#########)。 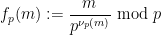 の場合、(1) の最初のコンポーネントは次のようになります:
の場合、(1) の最初のコンポーネントは次のようになります: 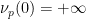 最終コンポーネント
最終コンポーネント 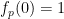 の典型的な例は次のようになります:
の典型的な例は次のようになります: 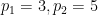 #興味深いはい、理由はわかりませんが、ここの装飾は基本的に子供向けゲーム「Fizz Buzz」のルールに従っています
#興味深いはい、理由はわかりませんが、ここの装飾は基本的に子供向けゲーム「Fizz Buzz」のルールに従っています
以上がテレンス・タオが、60 年来の幾何学の新たな問題にアプローチします。定期的な閉鎖舗装の問題に新たなブレークスルーがもたらされましたの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7549
7549
 15
15
 1382
1382
 52
52
 83
83
 11
11
 22
22
 90
90
 AI が数学研究を破壊する!フィールズ賞受賞者で中国系アメリカ人の数学者が上位 11 件の論文を主導 | テレンス・タオが「いいね!」しました
Apr 09, 2024 am 11:52 AM
AI が数学研究を破壊する!フィールズ賞受賞者で中国系アメリカ人の数学者が上位 11 件の論文を主導 | テレンス・タオが「いいね!」しました
Apr 09, 2024 am 11:52 AM
AI は確かに数学を変えつつあります。最近、この問題に細心の注意を払っている陶哲軒氏が『米国数学協会会報』(米国数学協会会報)の最新号を送ってくれた。 「機械は数学を変えるのか?」というテーマを中心に、多くの数学者が意見を述べ、そのプロセス全体は火花に満ち、ハードコアで刺激的でした。著者には、フィールズ賞受賞者のアクシャイ・ベンカテシュ氏、中国の数学者鄭楽軍氏、ニューヨーク大学のコンピューター科学者アーネスト・デイビス氏、その他業界で著名な学者を含む強力な顔ぶれが揃っている。 AI の世界は劇的に変化しています。これらの記事の多くは 1 年前に投稿されたものです。
 七角形数
Sep 24, 2023 am 10:33 AM
七角形数
Sep 24, 2023 am 10:33 AM
七角形の数は、七角形として表現できる数です。七角形は、7つの辺を持つ多角形です。七角形の数は、七角形(7角形)の連続した層の組み合わせで表現できます。七角形の数は、下の図でよりよく説明できます。したがって、
 画期的な CVM アルゴリズムが 40 年以上の計数の問題を解決します。コンピューター科学者がコインを投げて「ハムレット」を表す固有の単語を割り出す
Jun 07, 2024 pm 03:44 PM
画期的な CVM アルゴリズムが 40 年以上の計数の問題を解決します。コンピューター科学者がコインを投げて「ハムレット」を表す固有の単語を割り出す
Jun 07, 2024 pm 03:44 PM
数を数えるのは簡単そうに思えますが、実際にやってみるととても難しいです。あなたが野生動物の個体数調査を実施するために自然のままの熱帯雨林に運ばれたと想像してください。動物を見かけたら必ず写真を撮りましょう。デジタル カメラでは追跡された動物の総数のみが記録されますが、固有の動物の数に興味がありますが、統計はありません。では、このユニークな動物群にアクセスする最善の方法は何でしょうか?この時点で、今すぐ数え始めて、最後に写真から各新種をリストと比較すると言わなければなりません。ただし、この一般的なカウント方法は、数十億エントリに達する情報量には適さない場合があります。インド統計研究所、UNL、およびシンガポール国立大学のコンピューター科学者は、新しいアルゴリズムである CVM を提案しました。長いリスト内のさまざまな項目の計算を近似できます。
 MLPは一夜にして消滅した! MIT カリフォルニア工科大学とその他の革新的な KAN が記録を破り、DeepMind を打ち砕く数学的定理を発見
May 06, 2024 pm 03:10 PM
MLPは一夜にして消滅した! MIT カリフォルニア工科大学とその他の革新的な KAN が記録を破り、DeepMind を打ち砕く数学的定理を発見
May 06, 2024 pm 03:10 PM
一夜にして、機械学習のパラダイムが変わろうとしています。現在、深層学習の分野を支配しているインフラストラクチャは、ニューロンに活性化関数を配置する多層パーセプトロン (MLP) です。では、それを超えて、新たなルートはあるのでしょうか?ちょうど今日、MIT、カリフォルニア工科大学、ノースイースタン大学、その他の機関のチームが、新しいニューラル ネットワーク構造であるコルモゴロフ アーノルド ネットワーク (KAN) をリリースしました。研究者らは、学習可能な活性化関数をノード (ニューロン) からエッジ (重み) に移動することで、MLP に簡単な変更を加えました。論文アドレス: https://arxiv.org/pdf/2404.19756 この変更は一見すると根拠がないように見えます
 AI ペイントには依然として数学の知識が必要ですか?
Jun 12, 2023 pm 02:05 PM
AI ペイントには依然として数学の知識が必要ですか?
Jun 12, 2023 pm 02:05 PM
ビジョン 人工知能技術の発展に伴い、AI絵画が今話題になっています。深層学習アルゴリズムを使用することで、人工知能はリアルな画像を生成し、素晴らしい芸術作品を作成できます。これらの素晴らしい作品の背後には、数学的知識のサポートが切っても切り離せません。数学的モデルは AI ペイントにおいて重要な役割を果たします。一方では、数学的モデルを使用して画像情報を記述および表現し、コンピューターが画像を理解して処理できるようにします。一方、数学モデルは、画像の自動生成を実現するために深層学習モデルをトレーニングするためにも使用されます。ディープラーニング モデルによる高品質な画像生成 ディープラーニング モデルは AI ペイントの中核部分です。大量の画像データを学習し、多値のデータ処理を行うことで画像の特徴を識別しシミュレーションします。
 拡散モデルの背後にある数学は難しすぎて理解しにくいですか? Google は統一された視点でそれを明確にします
Apr 11, 2023 pm 07:46 PM
拡散モデルの背後にある数学は難しすぎて理解しにくいですか? Google は統一された視点でそれを明確にします
Apr 11, 2023 pm 07:46 PM
最近ではAIペイントが流行っていますね。 AI の描画機能に驚嘆している一方で、その中で拡散モデルが大きな役割を果たしているということはご存じないかもしれません。人気モデルOpenAIのDALL・E 2を例に挙げると、簡単なテキスト(プロンプト)を入力するだけで、1024*1024の高解像度画像を複数生成できます。 DALL・E 2 が発表されて間もなく、Google は、指定されたテキストの説明からシーンのリアルな画像を生成できるテキストから画像への AI モデルである Imagen をリリースしました。ほんの数日前、Stability.Ai はテキスト生成画像モデル Stable Diffusi を公開しました。
 「数学初心者」ChatGPT は人間の好みをよく理解しています。オンラインでの乱数の生成は宇宙に対する究極の答えです
Apr 01, 2023 am 11:48 AM
「数学初心者」ChatGPT は人間の好みをよく理解しています。オンラインでの乱数の生成は宇宙に対する究極の答えです
Apr 01, 2023 am 11:48 AM
ChatGPT は、乱数を生成する際の人間のトリックも理解します。 ChatGPT はデタラメなアーティストであり、誤った情報を広めているかもしれませんが、「数学者」ではありません。最近、メタ データ サイエンティストの Colin Fraser は、ChatGPT が真の乱数を生成することはできず、むしろ「人間の乱数」に近いことを発見しました。実験を通じて、フレイザー氏は「ChatGPTは42と7という数字がとても好きだ」と結論付け、ネチズンはこれは人間がこれらの数字をとても好むことを意味すると述べた。 ChatGPT も「宇宙への究極の答え」が大好きです。彼のテストでは、フレイザーが入力したプロンプトは次のとおりです。「乱数を選択してください」
 Google Brain の研究者たちは、日中は働き、夜は研究を行い、数十年にわたって数学コミュニティを困惑させてきた予想を解決しました。
Apr 12, 2023 am 09:49 AM
Google Brain の研究者たちは、日中は働き、夜は研究を行い、数十年にわたって数学コミュニティを困惑させてきた予想を解決しました。
Apr 12, 2023 am 09:49 AM
2022年10月中旬、ジャスティン・ギルマーは東海岸にあるラトガース大学の数学者でかつての指導者であるマイケル・サックスを訪ねるためにカリフォルニアからニューヨークに飛んだ。回想の間、彼らは数学について話しませんでした。実際、ギルマーは 2015 年にラトガース大学で博士号を取得して以来、数学について真剣に考えていませんでした。その時、彼は学界でのキャリアを追求しないことを決意し、独学でプログラミングを学び始めました。サックスとの夕食をとりながら、ギルマーはグーグルでの仕事、つまり機械学習と人工知能についてメンターに語った。キャンパス内の小道を歩きながら、ギルマーさんは 2013 年に 1 年以上この道を歩いていたことを思い出しました。




