
行列の乗算の実行過程を3Dで表示できれば、当時の行列の乗算の学習はそれほど難しくなくなります。
現在、行列乗算は機械学習モデルの構成要素であり、さまざまな強力な AI テクノロジーの基礎となっており、その実行方法を理解することは、この AI とこのますますインテリジェントになるシステムの世界をより深く理解するのに間違いなく役立ちます。
PyTorch ブログのこの記事では、行列の乗算と行列の乗算の組み合わせを視覚化するツールである mm を紹介します。
mm は 3 つの空間次元すべてを使用するため、通常の 2 次元チャートと比較して、mm は直感的に表示してアイデアを刺激するのに役立ち、認知的オーバーヘッドの使用が少なくなります。視覚的および空間的思考。
そして、行列の乗算を組み合わせる 3 次元と、トレーニングされた重みを読み込む機能を組み合わせることで、mm は大きな複合式 (アテンション ヘッドなど) を視覚化し、その実際の動作パターンを観察できます。
mm は完全にインタラクティブで、ブラウザーまたはノートブック iframe で実行され、完全な状態が URL に保存されるため、リンクは共有可能なセッションになります (この記事のスクリーンショットとビデオの両方にはリンクがあります。ツールで対応するビジュアライゼーションを開くことができます。詳細については、元のブログを参照してください)。このリファレンス ガイドでは、利用可能なすべての機能について説明します。
ツールのアドレス: https://bhosmer.github.io/mm/ref.html
元のブログのテキスト: https:// pytorch .org/blog/inside-the-matrix
この記事では、最初にいくつかの単純な行列の乗算と式を視覚化することで直感を構築する視覚化方法を紹介し、次にいくつかの拡張例を詳しく見ていきます。 :
はじめに: なぜこの視覚化が優れているのでしょうか?
ウォームアップ: アニメーション - 標準的な行列乗算分解の作業プロセスを確認します。
ウォームアップ: 式 - いくつかの概要を見てみましょう基本的な式 数式の構成要素
詳細なアテンション ヘッド: GPT-2 から NanoGPT までの 1 対のアテンション ヘッドの構造、値、および計算動作の詳細な観察
アテンションの並列化: 最近の Blockwise Parallel Transformer 論文の例を使用して、アテンション ヘッドの並列化を視覚化します。
アテンション層のサイズ: アテンション層全体を単一の構造として視覚化した場合、アテンション層の MHA 半分と FFA 半分を合わせるとどのように見えるでしょうか。自己回帰デコードプロセス中に画像はどのように変化しますか?
LoRA: このアテンション ヘッド アーキテクチャの詳細についての視覚的な説明
1 はじめに
mm の視覚化アプローチは、行列の乗算が本質的に 3 次元の演算であるという前提に基づいています。
言い換えると:
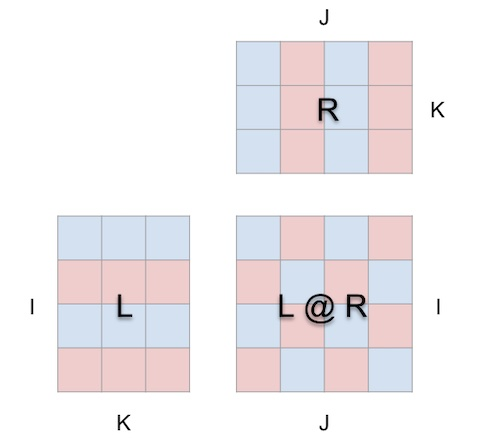

2 ウォームアップ: アニメーション
より複雑な例に入る前に、この視覚化スタイルがどのようなものかを見て、道具。2a 内積
最初に古典的なアルゴリズムを見てみましょう - 対応する左行と右列のドット積を計算することによって、各結果要素を計算します。ここのアニメーションからわかるように、乗算された値のベクトルは立方体の内部をスイープし、そのたびに対応する位置に合計結果が表示されます。
ここで、L には 1 (青) または -1 (赤) で埋められた行のブロックがあり、R には同様に埋められた列のブロックがあります。ここで、k は 24 であるため、結果の行列 (L @ R) の青の値は 24、赤の値は -24 になります。 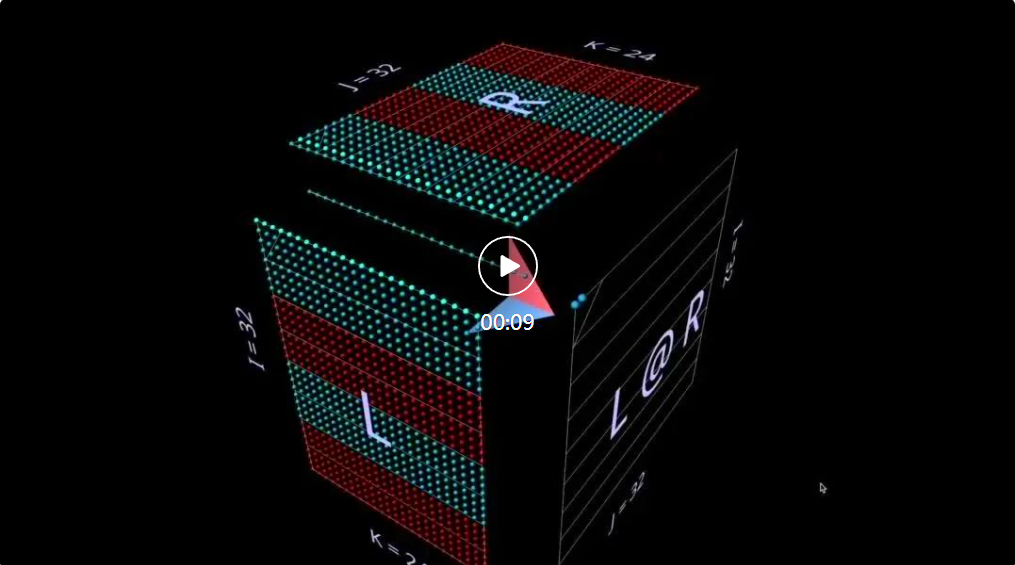
2b 行列ベクトル積
行列ベクトル積に分解します 行列乗算は垂直面のように見えます (左のパラメーターと右側のパラメータの各列の積)、立方体の内部を水平方向にスイープし、結果に列をプロットします。例は単純ですが、興味深いです。  例として、ランダムに初期化されたパラメーターを使用すると、中央の行列とベクトルの積が垂直パターンを強調表示することに注意してください。これは、各中間値が左側のパラメーターのスケールされたコピーの列であるという事実を反映しています。
例として、ランダムに初期化されたパラメーターを使用すると、中央の行列とベクトルの積が垂直パターンを強調表示することに注意してください。これは、各中間値が左側のパラメーターのスケールされたコピーの列であるという事実を反映しています。
ランダムに初期化されたパラメータに切り替えると、行列とベクトルの積のようなパターンが表示されます -- 今回は除きます水平モードでは、各中間ベクトル行列積が右側のパラメーターの行スケールされたコピーであるという事実に対応します。 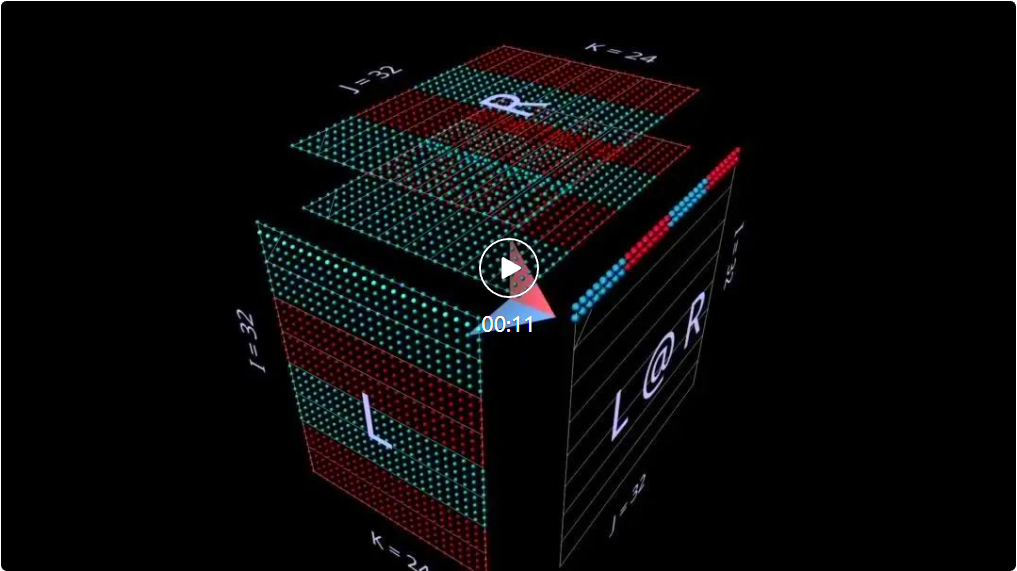 行列の乗算がパラメータの順位和構造をどのように表現するかを考えるとき、両方のモードが計算中に同時に発生することを想像すると役に立ちます。
行列の乗算がパラメータの順位和構造をどのように表現するかを考えるとき、両方のモードが計算中に同時に発生することを想像すると役に立ちます。
ここに別の例を示します。ベクトル行列積を使用して直感を構築すると、単位行列が 45 度の角度で置かれた鏡のように機能し、対応するパラメーターと結果を反映することがわかります。
3 番目の平面分解では、ベクトルの外積を点ごとに合計することによって、k 軸に沿った行列の乗算結果を計算します。ここでは、外積平面が立方体を「後ろから前に」スイープし、結果に累積していることがわかります。
ランダムに初期化された行列を使用して、この分解を実行します。値を確認するだけでなく、ランク 1 の各外積が結果に加算されるため、結果のランクの累積も確認できます。 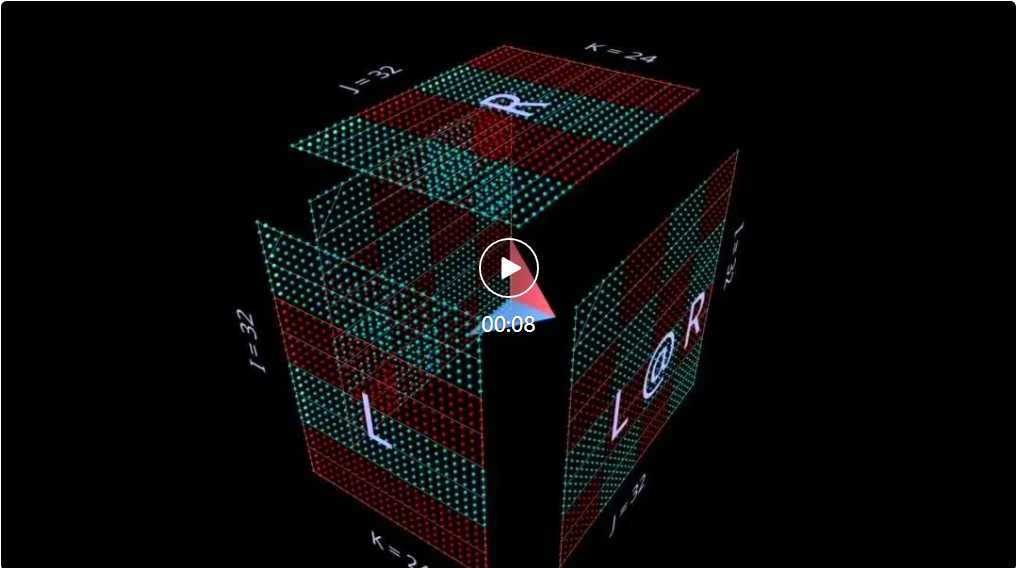 これは、近似された行列が低ランクの場合に、「低ランク因数分解」(つまり、深さ次元でより小さいパラメーターを使用して行列の乗算を構築することで行列を近似する) がより適切に機能する理由も直感的に説明しています。マトリックス、最高の効果。これは、後で説明する LoRA です:
これは、近似された行列が低ランクの場合に、「低ランク因数分解」(つまり、深さ次元でより小さいパラメーターを使用して行列の乗算を構築することで行列を近似する) がより適切に機能する理由も直感的に説明しています。マトリックス、最高の効果。これは、後で説明する LoRA です:
このアプローチは複合式に対して適切に拡張できることがわかりました。重要なルールは単純です: 部分式 (サブ) 行列乗算は、親行列乗算と同じレイアウト制約を受ける別の立方体です。部分行列乗算の結果面は、共有行列と同様に、親行列乗算のパラメータ面でもあります。共有電子。
これらの制約内で、必要に応じて部分行列乗算のさまざまな側面を調整できます。ここではツールのデフォルト スキームが使用されており、凸面と凹面の立方体が交互に生成されます。このレイアウトは実際にはうまく機能し、オクルージョンを最小限に抑えながらスペースを最大化します。 (ただし、レイアウトは完全にカスタマイズ可能です。詳細については、mm ツールのページを参照してください。)
このセクションでは、機械学習モデルの主要な構成要素のいくつかを視覚化して、読者がこの視覚的表現に慣れ、新たな知識を得ることができるようにします。そこからの直感。
3a 左結合式
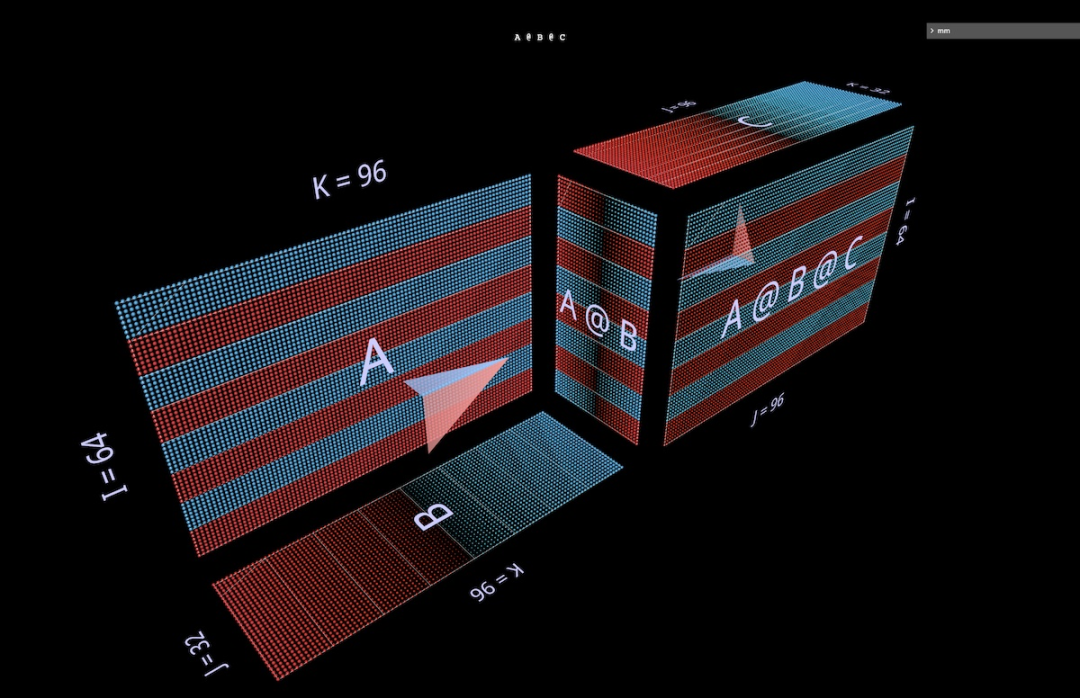
以下に、(A @ B) @ C という形式の 2 つの式を紹介します。それぞれに独自の形状と特徴があります。 (注: mm は行列の乗算が左結合であるという規則に従っているため、(A @ B) @ C は単純に A @ B @ C と書くことができます。)
まず、A @ B @ C に非常に特徴的なものを与えます。 「隠れ次元」が「入力」または「出力」次元よりも広い FFN 形状。 (具体的には、この例では、B の幅が A または C の幅よりも大きいことを意味します。)
単一行列の乗算の例と同様に、浮動矢印は結果の行列を指します。 fletching 左側のパラメータから、赤い fletching は右側のパラメータから得られます。

B の幅が A または C の幅より小さい場合、次の形状と同様に、A @ B @ C の視覚化にボトルネックが発生します。オートエンコーダー。
#3b 右連想式

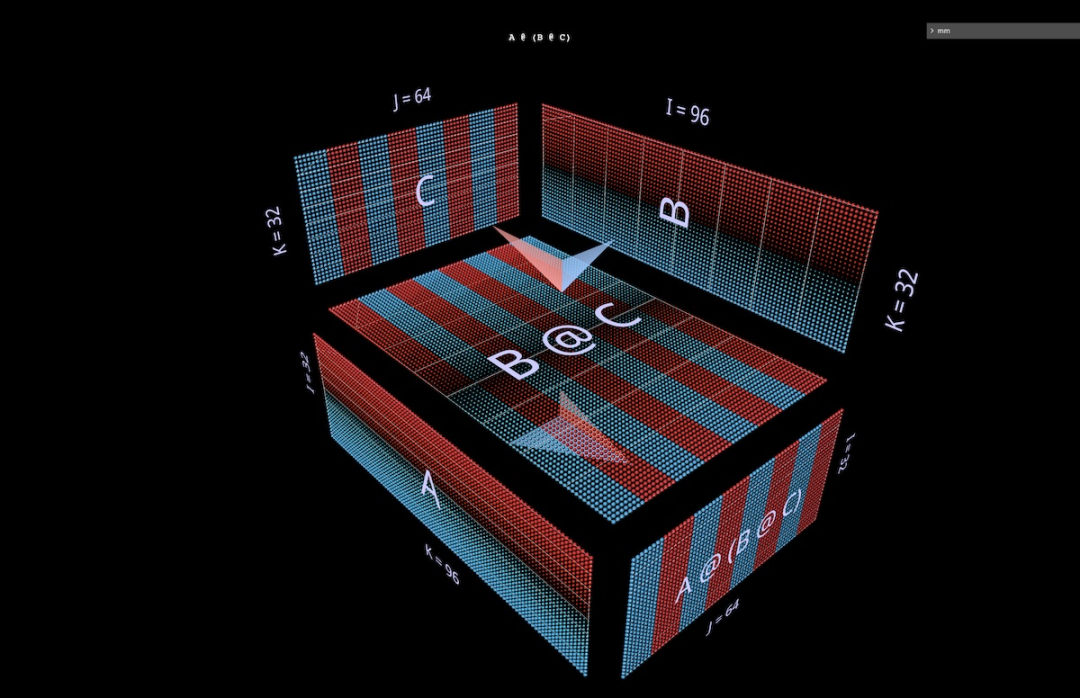
は、左の結合式の水平方向の展開に似ています。ルート式の左のパラメータから始まると言えますが、右の結合式チェーンは、ルート式の右のパラメータから開始して垂直に拡張されます。ルート式 。
MLP が右結合形式で形成されている場合があります。この場合、右側は列入力であり、重み層は右から左に実行されます。上に示した 2 層 FFN の例の行列を (適切な転置後) 使用すると、次のようになります。C が入力、B が最初の層、A が 2 番目の層になります。また、矢羽根の色 (左が青、右が赤) に加えて、左右のパラメータを区別する 2 番目の視覚的手がかりは、その方向です。左側は結果の行と同一平面上にあります。これらは同じ軸 (i) に沿って積み重ねられています。たとえば、上記の (B @ C) では、両方のヒントから B が左側のパラメーターであることがわかります。
 3c バイナリ式
3c バイナリ式
このような形状 (A @ B) @ (C @ D) の最も単純な式をここに視覚化します:
3d ちょっとしたメモ:パーティショニングと並列処理
最初の例は、典型的な「データ並列」パーティショニングを上記の左結合多層ボトルネックの例に適用するものです。 i に沿って分割し、最初の左側のパラメーター (「バッチ」) とすべての中間結果 (「アクティブ化」) をセグメント化しますが、後続のパラメーター (「重み」) はセグメント化しません。このジオメトリにより、次の式が明らかになります。アクターはセグメント化され、そのまま残ります:
2 番目の例は、明確な幾何学的サポートがなければ直観的に理解するのが困難です。これは、左側の部分式を次のように分割することによってバイナリ式を並列化する方法を示しています。 j 軸、i 軸に沿った右側の部分式、および k 軸に沿った親式:


それでは、GPT-2 の注目のヘッド、特に 5 層 NanoGPT の 4 番目のヘッドの「gpt2」(小さい) 構成を見てみましょう (層数 = 12、ヘッド数 = 12、番号埋め込みの数 = 768)、HuggingFace 経由で OpenAI からの重みを使用します。入力アクティベーションは、256 個のトークンを含む OpenWebText トレーニング サンプルのフォワード パスから取得されます。
この特定のヘッダーには特別なことは何もありません。これが選択された主な理由は、非常に一般的な注意パターンを計算し、アクティベーションが構造化され、いくつかの興味深いテクスチャを表示するモデルの中央に位置しているためです。
4a 構造
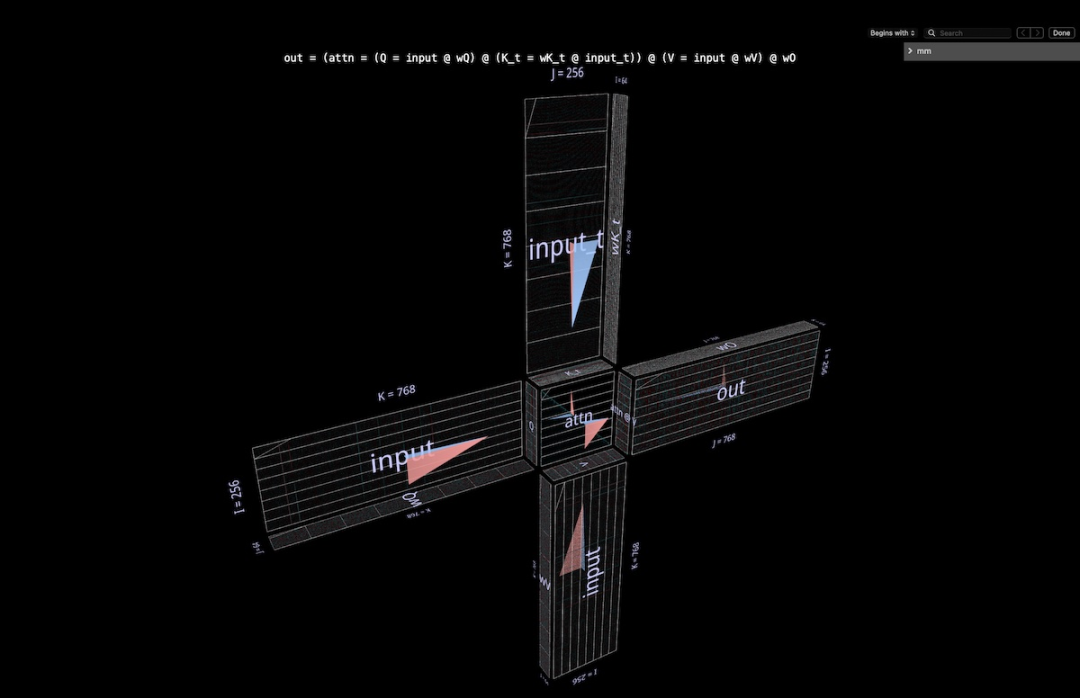
この完全なアテンションヘッドは、入力から始まり入力で終わる単一の複合式として視覚化されます。投影出力。 (注: 自己充足性を確保するために、Megatron-LM についてここで説明されているように、出力投影はヘッドごとに実行されます。)
この計算には 6 つの行列乗算が含まれます:
Q = input @ wQ// 1K_t = wK_t @ input_t// 2V = input @ wV// 3attn = sdpa(Q @ K_t)// 4head_out = attn @ V // 5out = head_out @ wO // 6
ここで何が行われているかを簡単に説明します:
風車の羽根は行列乗算 1、2、3、6 です。前者のグループは Q への入力の内部射影です。 K と V; 後者は attn@V から埋め込み次元への外側の射影です。
中央には 2 つの行列乗算があり、最初は注意スコア (後ろの凸立方体) を計算し、次にそれらを使用して値ベクトルに基づいて出力トークンを取得します。 (前面の凹面立方体) 。因果関係とは、注意スコアが下三角を形成することを意味します。
ただし、読者は、スクリーンショットや以下のビデオを見るだけでなく、このツールを自分で詳しく調べて、その構造とそれを流れる計算プロセス、実際の値。
4b 合計値の計算
アテンションヘッドの計算過程のアニメーションです。具体的には、
sdpa (input @ wQ @ K_t) @ V @ wO
(つまり、K_t と V が事前に計算されている上記の行列乗算 1、4、5、6) をベクトル行列積の融合として検討しています。チェーンが計算されます。シーケンス内の各項目は、1 つのステップで入力から出力までアテンションを通過します。このアニメーションのその他のオプションについては、並列化に関するセクションで後ほど説明しますが、最初に計算された値が何を示すかを見てみましょう。 
多くの興味深いことがわかります:
注意の計算について説明する前に、低ランクのQ、K_tさんのフォームは素晴らしいですね。 Q @ K_t ベクトル行列積アニメーションを拡大すると、さらに鮮明に見えます。Q と K の多数のチャネル (埋め込まれた位置) はシーケンス内で多かれ少なかれ一定であるように見えます。これは、有用な注意信号であることを意味します。少数の組み込みドライバーのセットによってのみ生成される可能性があります。この現象を理解して活用することは、SysML ATOM トランス効率化プロジェクトの一部です。
おそらく最もよく知られているのは、アテンション マトリックスに表示される強力だが不完全な対角線です。これは、このモデルの多くのアテンションヘッド (および多くのトランスフォーマー) に現れる一般的なパターンです。これにより、局所的な注目を集めることができます。出力トークンの位置の直前にある小さな近傍の値トークンが、出力トークンのコンテンツ パターンを大きく決定します。
ただし、この近傍のサイズとその中の個々のトークンの影響は大きく異なります。これは、アテンション グリッドの斜めから外れた霜や波にも見られます。アテンション行列がシーケンスに沿って下降するにつれて、attn[i] @ V ベクトルと行列の積平面に見られるパターン。
ただし、注目に値するのはローカル近傍だけではないことに注意してください。アテンション グリッドの左端の列 (シーケンスの最初のトークンに対応) は完全に非ゼロで埋められています。 (ただし変動する) 値。これは、各出力トークンが最初の値トークンによってある程度影響を受けることを意味します。
さらに、現在のトークン近傍と最初のトークンとの間の注意スコアの優位性には、不正確ではあるが認識できる変動があります。この振動の周期はさまざまですが、一般に、最初は短く、シーケンスが下に進むにつれて長くなります (同様に、因果関係を考慮すると、関連する行ごとの候補アテンション トークンの数に関連します)。
(attn @ V) がどのように形成されるかを理解するには、注意だけに注目しないことが重要です。V も同様に重要です。各出力項は V ベクトル全体の加重平均です。attention が完全な対角線である極端な場合、 attn @ V は V の正確なコピーにすぎません。ここでは、よりテクスチャーのあるものが見られます: 特定のトークンが注目行の連続サブシーケンスで高いスコアを獲得する目に見えるバンド状の構造が、明らかに V に似ていますが、対角線が太いマトリックスに重ねられています。 (補足: mm リファレンス ガイドによると、長押しするか Control キーを押しながらクリックすると、視覚化要素の実際の数値が表示されます。)
私たちは中間層 (層 5) にいるため、このアテンション ヘッドへの入力は中間表現であり、元のトークン化されたテキストではないことに注意してください。したがって、入力に見られるパターンは、それ自体が考えさせられるものです。特に、強い垂直線は特定の埋め込み位置であり、その値はシーケンスの長い範囲にわたって均一に高い振幅を持ち、場合によってはほぼ完全になります。
しかし、興味深いのは、入力シーケンスの最初のベクトルが一意であり、これらの高振幅列のパターンを破るだけでなく、ほぼすべての位置値 (サイド) に異常な値が含まれていることです。注: ここでは視覚化されていませんが、このパターンは複数のサンプル入力で繰り返し表示されます)。
注: 最後の 2 つの点に関して、ここで視覚化されているのは 1 つのサンプル入力に対する計算であることを繰り返しておきます。実際には、各頭部には、かなり大規模なサンプルのセットにわたって一貫して (同一ではないにせよ) 表現される特徴的なパターンがあることがわかります。しかし、アクティベーションを含むビジュアライゼーションを見るときは、入力の完全な分布を覚えておく必要があります。それがインスピレーションを与えるアイデアや直感に微妙な影響を与える可能性があります。
最後に、もう一度アニメーションを直接探索することをお勧めします。
4c アテンションヘッドには興味深い違いがたくさんあります
続行する前に、セックスの詳細な動作を理解するためにモデルを単純に研究することの有用性を示す別のデモンストレーションを示します。 。
こちらもGPT-2の注目ヘッドです。その動作パターンは、レベル 5 ヘッド 4 の動作パターンとはかなり異なります。モデルの非常に異なる部分にあるため、ご想像のとおりです。このヘッダは最初のレイヤにあります: レイヤ 0 のヘッダ 2:

注目すべき点:
このヘッダに関する注意力の分布は非常に均一です。これには、アニメーションに示すように、比較的重み付けされていない V (または V の適切な因果接頭語) の平均を attn@V の各行に配信する効果があります。注意スコアの三角形を下に移動すると、attn[i] @ Vベクトル - 単に縮小された V のコピーではなく、小さな変動を伴う行列積。徐々に明らかになります。
attn @ V は、驚くべき垂直方向の均一性を持っています。値の同じパターンが、シーケンス全体に埋め込まれた大きな柱状領域に持続します。これらは、各トークンによって共有されるプロパティと考えることができます。
補足: 一方で、注意が非常に均等に分散される効果を考えると、attn@V にはある程度の一貫性があることが期待されるかもしれません。しかし、各行はシーケンス全体ではなく、V の因果的なサブシーケンスで構成されています。これにより、シーケンスを下に進むにつれて徐々に変形するなど、さらなる変更が生じないのはなぜでしょうか?目視検査では、V がその長さに沿って均一ではないことが示されているため、答えはその値の分布のより微妙な特性にあるはずです。
最後に、外部投影後、このヘッドの出力は垂直方向により均一になるはずです。
強い印象を得ることができます。このアテンション ヘッドによって伝えられる情報のほとんどは、シーケンス内の各トークンが共有する属性で構成されています。その出力投影重みの構成により、この直観が強化されます。
全体として、私たちは不思議に思わずにはいられません:この注意頭によって生成された非常に規則的で高度に構造化された情報は、少し...あまり豪華ではないコンピューティング手段を通じて取得された可能性があります。これは決して未開拓の領域ではありませんが、計算信号の視覚化の明瞭さと豊富さは、新しいアイデアの生成と既存のアイデアの推論の両方に非常に役立ちます。
4d はじめに戻る: 自由不変性
振り返ってみると、繰り返し説明する必要があります。注意と注意の重要な複合操作を視覚化できる理由です。重要な代数的特性 (パラメーターの形状がどのように制約されるか、どの平行軸がどの演算と交差するかなど) については追加の思考を必要としないため、直感的に操作できます。それらは、特別なものではなく、視覚化されたオブジェクトの幾何学的特性から直接生じます。覚えておくこと、ルール。
たとえば、これらのアテンションヘッドの視覚化では、次のことがはっきりとわかります:
Q は attn @ V と同じ長さを持ち、K は同じ長さを持ちます。 V として、これらのペアの長さは互いに独立しています。
Q は K と同じ幅を持ち、V は attn @ V と同じ幅を持ち、これらのペアの幅はは互いに独立しています。
これらの構造は、複合構造内のどこに構造コンポーネントが配置され、その方向がどのようなものであるかという単純な結果として、構造的に現実のものとなります。
この「自由な性質」の利点は、典型的な構造のバリエーションを調査するときに特に役立ちます。わかりやすい例は、自己回帰トークン内の単一行の注目度の高い行列を一度にデコードすることです。

5 並列化されたアテンション
上記の 5 つのレイヤーのうちヘッド 4 のアニメーションは、アテンション ヘッドの 6 つの行列乗算のうち 4 つを視覚化します。
これらはベクトル行列積の融合チェーンとして視覚化されており、幾何学的直観が確認されています。入力から出力までの左側の融合チェーン全体が共有の i 軸に沿って階層化されており、並列化できます。
5a 例: i に沿った分割
実際に計算を並列化するには、入力を i 軸に沿ってブロックに分割します。特定の軸を特定の数のブロックに分割することを指定することで、ツールでこの分割を視覚化できます。これらの例では 8 が使用されていますが、この数について特別なことは何もありません。
これに加えて、この視覚化は、各並列計算が完全な wQ (内部射影用)、K_t と V (注意用)、および wO (外部射影用) を必要とすることを明確に示しています。これらの行列の分割されていない次元:

#5b 例: デュアル分割
複数の軸に沿った分割の例もここに示します。この目的を達成するために、ここでは、フラッシュ アテンションなどのいくつかの研究結果に基づいた、この分野における最近のイノベーション、つまりブロック並列トランスフォーマー (BPT) を視覚化することを選択します。 pdf/2305.19370.pdfまず、BPT は上記のように i に沿って分割し、実際にシーケンスのこの水平分割を注目層 (FFN) の残りの半分まで拡張します。 (これを視覚化したものは後で示します。) このコンテキストの長さの問題を完全に解決するには、MHA に 2 番目のパーティションを追加します。これは、注意計算自体のパーティションです (つまり、Q@K_t の j 軸に沿ったもの)。パーティション)。これら 2 つのパーティションを組み合わせると、注意がブロックのグリッドに分割されます:

アテンション層 (MHA) の前半部分は、次の理由によりサイズが大きいことが知られています。二次複雑さ 高い計算要件がありますが、後半 (FFN) にも、隠れ次元の幅 (通常、モデルの埋め込み次元の幅の 4 倍) があるため、独自の要件があります。完全な注目層のバイオマスを視覚化すると、層の 2 つの半分が互いにどのように比較されるかを直感的に理解するのに役立ちます。
6a 完全なアテンション レイヤーの視覚化以下は完全なアテンション レイヤーです。前半 (MHA) が後ろ、後半 (FFN) が後ろにあります。フロント。繰り返しますが、矢印は計算の方向を指します。
注:
このビジュアライゼーションは、単一のアテンション ヘッドを示しているのではなく、中央の二重行列乗算の周りのスライスされていない Q/K/V の重みと投影を示しています。もちろん、これは完全な MHA 操作を忠実に視覚化したものではありません。しかし、ここでの目的は、層の 2 つの半分で実行される相対的な計算量ではなく、層の 2 つの半分の相対的な行列サイズをより明確に把握することです。 (また、ここでの重みは実際の重みではなくランダムな値を使用します。)
ここで使用される寸法は、ブラウザーが (相対的に) 操作できるように縮小されていますが、比率は同じままです (小さいから小さい)。 NanoGPT 構成): モデルの埋め込み次元 = 192 (元は 768)、FFN 埋め込み次元 = 768 (元は 3072)、シーケンス長 = 256 (元は 1024) ただし、シーケンスの長さはモデルに基本的な影響を与えません。 (視覚的には、シーケンスの長さの変化は入力ブレードの幅の変化として現れ、その結果、注目のサイズと下流の垂直面の高さが変化します。)

Blockwise Parallel Transformer について簡単に説明します。ここでは、アテンション レイヤー全体のコンテキストで BPT を視覚化するための並列化ソリューションを示します (各ヘッダーは上記と同様に省略されています)。 i (シーケンス ブロック) に沿った分割が MHA と FFN の半分にどのように拡張されるかに特に注意してください。

の分割 この視覚化方法は、上で説明したものに直交する追加のパーティションを提案します。注目層の FFN 半分で、二重行列の乗算 (attn_out @ FFN_1) @ FFN_2 を分割し、最初に j @ FFN_1 に沿って attn_out を実行し、次に後続の行列を実行します。 k と FFN_2 の乗算。この分割により 2 つの FFN 重み層がスライスされ、部分的な結果の最終的な合計が犠牲になって、計算に関与する各コンポーネントの容量要件が削減されます。 この分割方法を分割されていないアテンション レイヤーに適用すると、次のようになります。 BPT 分割レイヤーに適用すると、次のようになります。 : 6d 一度に 1 つのトークンをデコードするプロセスを視覚化する 一度に 1 つのトークンの自己回帰デコード プロセス内、クエリ ベクトルは単一のトークンで構成されます。この場合、アテンション レイヤーがどのように見えるかを頭の中で想像すると有益です。つまり、巨大なタイル状のウェイト プレーン全体に 1 つの埋め込み行が表示されます。 このビューは、アクティベーションと比較して重みの巨大さを強調することに加えて、MHA のマルチプレクサ/デマルチプレクサの計算ではあるものの、K_t と V が 6 層 MLP で動的に生成された層と同様に機能するという概念も思い出させます。 7 LoRA 最近の LoRA 論文「LoRA : 大規模言語モデルの低ランク適応」 」では、微調整中に導入される重み δ が低ランクであるという考えに基づいた効率的な微調整手法が説明されています。論文によると、これにより「適応中に高密度層の変化のランク分解行列を最適化することで、ニューラル ネットワーク内の一部の高密度層を間接的に訓練できるようになります。同時に、事前に訓練された重みを凍結したままにすることができます。」 7a 基本的な考え方 つまり、重要なステップは、行列自体ではなく重み行列の係数をトレーニングすることです。つまり、I x K テンソルと K x J の行列の乗算です。テンソル I x J 重みテンソルを置き換えるには、K が小さい値であることを確認する必要があります。 K が十分に小さい場合、サイズの点で大きな利点がある可能性がありますが、トレードオフもあります。K を小さくすると、製品が表現できるランクも低下します。ここでは、サイズの節約と結果への構造的影響を例として示します。ここでは、128 x 4 の左側のパラメーターと 4 x 128 の右側のパラメーターのランダムな行列の乗算、つまり、ランク 4 ブレークを持つ 128 x 128 の行列です。下。 L@R の垂直モードと水平モードに注意してください: #7b LoRA をアテンション ヘッドに適用します LoRA はこれを適用します。分解メソッドを微調整プロセスに適用する方法は次のとおりです。 微調整する各重みテンソルに対して低ランクの分解を作成し、元の要素を維持したままその因子をトレーニングします。重みを凍結; 微調整後、低ランク因数の各ペアを乗算して元の重みテンソルの形状の行列を取得し、それを元の事前トレーニングされた重みに追加します。テンソル。 以下の視覚化は、重みテンソル wQ、wK_t、wV、wO が低ランク分解 wQ_A @ wQ_B などに置き換えられたアテンション ヘッドを示しています。視覚的には、因子行列は風車のブレードの端に沿った低いフェンスとして表示されます。 




以上が3D の観点から行列の乗算を洞察する、AI の考え方は次のとおりですの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。