パラメータがほぼ半分であるため、パフォーマンスは Google Minerva に近く、別の大規模な数学モデルはオープンソースです

現在、さまざまなテキスト混合データでトレーニングされた言語モデルは、非常に一般的な言語理解および生成機能を示し、さまざまなアプリケーションに適応する基本モデルとして使用できます。オープン ダイアログや指示追跡などのアプリケーションでは、自然テキスト配布全体にわたってバランスの取れたパフォーマンスが必要なため、汎用モデルが好まれます。

ただし、特定のドメイン (医療、金融、科学など) 内でパフォーマンスを最大化したい場合は、特定の計算コストでドメイン固有の言語モデルを利用できる場合があります。機能を提供したり、より低い計算コストで特定のレベルの機能を提供したりできます。

プリンストン大学、EleutherAI などの研究者は、数学的問題を解決するためにドメイン固有の言語モデルをトレーニングしました。彼らは次のように考えています: 第一に、数学的問題を解決するには、大量の専門的な事前知識とのパターン マッチングが必要であるため、ドメイン適応性のトレーニングには理想的な環境です。第二に、数学的推論自体が AI の中核的なタスクであり、最後に、実行する能力です。強力な数学的推論 言語モデルは、報酬モデリング、推論強化学習、アルゴリズム推論など、多くの研究トピックの上流にあります。

したがって、彼らは、Proof-Pile-2 の継続的な事前トレーニングを通じて言語モデルを数学に適応させる方法を提案しています。 Proof-Pile-2 は、数学関連のテキストとコードを組み合わせたものです。このアプローチを Code Llama に適用すると、数学的機能が大幅に向上した 7B および 34B の基本言語モデルである LLEMMA が作成されます。

論文アドレス: https://arxiv.org/pdf/2310.10631.pdf

#プロジェクト アドレス: https://github.com/EleutherAI/math-lm

LLEMMA 7B の 4 ショット Math パフォーマンスは Google Minerva 8B をはるかに上回り、LLEMMA 34B はパフォーマンスはミネルバ 62B に近く、パラメーターはほぼ半分です。

具体的には、この記事の貢献は次のとおりです:

• 1. トレーニング済みLLEMMA モデル: 数学専用の 7B および 34B 言語モデルを公開しました。 LLEMMA モデルは、MATH で公開されている最先端の基本モデルです。
• 2. 特に数学に関連する 11B コード トークンを含むデータセットである AlgebraicStack をリリースしました。
• 3. LLEMMA は、Python インタプリタと形式的定理証明器という計算ツールを使用して数学的問題を解決できることが実証されています。
• 4. 以前の数学言語モデル (ミネルバなど) とは異なり、LLEMMA モデルはオープンエンドです。研究者らはトレーニング データとコードを一般に公開しました。これにより、LLEMMA は数学的推論における将来の研究のためのプラットフォームになります。

メソッドの概要

LLEMMA は、数学に特化した 70B および 34B 言語モデルです。これは、Proof-Pile-2 でコード Llama の事前トレーニングを継続することによって取得されます。

#データ: プルーフパイル-2

研究者らは、科学論文、数学を含むネットワーク データ、数学コードを組み合わせた 550 億トークンである Proof-Pile-2 を作成しました。 Proof-Pile-2 のナレッジ期限は、リーン プルーフステップ サブセットを除き、2023 年 4 月です。

数値シミュレーション、コンピューター代数システム、形式定理証明器などの計算ツールは、数学者にとってますます重要になっています。そこで研究者らは、数値数学、記号数学、形式数学をカバーする 17 言語のソース コードを含む 11B トークン データ セットである AlgebraicStack を作成しました。データセットは、スタック、GitHub パブリック リポジトリ、および正式な証明ステップ データからのフィルタリングされたコードで構成されます。表 9 は、AlgebraicStack の各言語のトークン数を示しています。

AlgebraicStack 内の各言語のトークンの数。

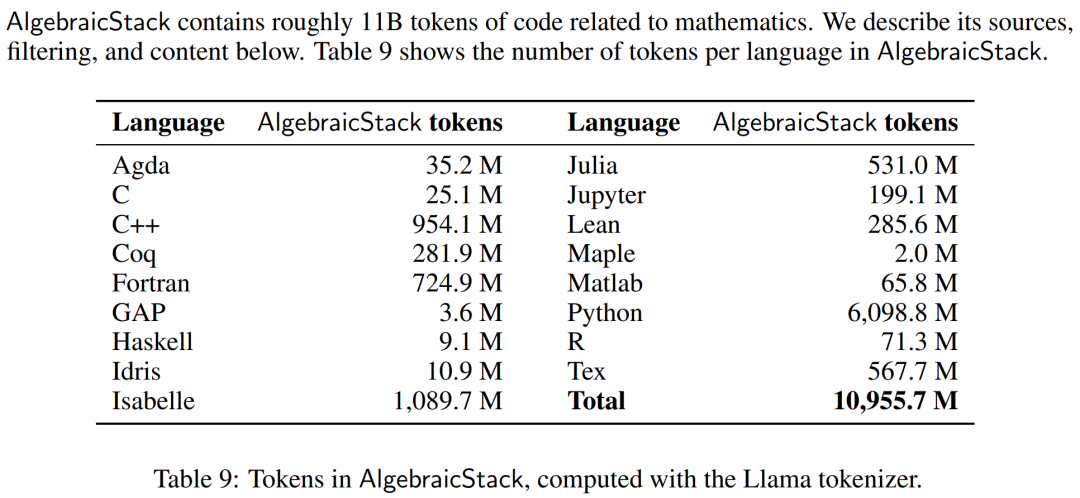
研究者らは、数学的コンテンツをフィルター処理した高品質の Web ページで構成される 15B トークン データセットである OpenWebMath を使用しました。 OpenWebMath は、数学関連のキーワードと分類子ベースの数学スコアに基づいて CommonCrawl Web ページをフィルタリングし、数学フォーマット (LATEX、AsciiMath など) を保持し、追加の品質フィルター (プレキシティ、ドメイン、長さなど) とほぼ重複を含みます。

これに加えて、研究者らは、LLaMA トレーニング データセットのオープン レンディションである RedPajama の ArXiv サブセットも使用しました。 ArXiv サブセットには 29B チャンクが含まれています。トレーニング混合物は少量の一般的なドメイン データで構成され、正則化機能として機能します。 LLaMA 2 の事前トレーニング データセットはまだ公開されていないため、研究者らは代替トレーニング データセットとして Pile を使用しました。

モデルとトレーニング

各モデルは Code Llama から初期化され、さらに Code Llama 2 から初期化されます。デコンダのみのトランスフォーマ構造を使用し、500B コード トークンでトレーニングされます。研究者らは、標準的な自己回帰言語モデリング目標を使用して、Proof-Pile-2 で Code Llama モデルのトレーニングを続けました。ここで、LLEMMA 7B モデルには 200B トークンがあり、LLEMMA 34B モデルには 50B トークンがあります。

研究者らは、GPT-NeoX ライブラリを使用して、256 個の A100 40GB GPU 上で bfloat16 混合精度で上記 2 つのモデルをトレーニングしました。彼らは、LLEMMA-7B にはワールド サイズ 2 のテンソル並列処理を、34B にはワールド サイズ 8 のテンソル並列処理を使用しました。また、データ並列レプリカ全体で ZeRO Stage 1 シャード オプティマイザーの状態を使用しました。 Flash アテンション 2 は、スループットを向上させ、メモリ要件をさらに削減するためにも使用されます。

LLEMMA 7B は、42,000 ステップ、グローバル バッチ サイズ 400 万トークン、コンテキスト長 4096 トークンでトレーニングされています。これは、A100 の 23,000 時間に相当します。学習率は 500 ステップ後に 1·10^−4 まで上昇し、48,000 ステップ後には最大学習率の 1/30 まで余弦的に減衰します。

LLEMMA 34B は 12,000 ステップでトレーニングされており、グローバル バッチ サイズも 400 万トークン、コンテキストの長さは 4096 です。これは、A100 の 47,000 時間に相当します。学習率は 500 ステップ後に 5・10^−5 まで上昇し、その後ピーク学習率の 1/30 まで減衰します。

評価結果

実験部分では、研究者はLLEMMAが数学テキストの基本モデルとして使用できるかどうかを評価することを目的としました。彼らは、LLEMMA モデルを比較するために少数ショット評価を利用し、数学的タスクの教師ありサンプルで微調整されていない SOTA モデルに主に焦点を当てています。

研究者らはまず、思考連鎖推論と多数決法を使用して、LLEMMA の数学的問題を解決する能力を評価しました。評価ベンチマークには、MATH と GSM8k が含まれていました。次に、少数ショット ツールの使用と定理の証明を検討します。最後に、メモリとデータの混合の影響について研究します。

思考連鎖 (CoT) を使用して数学の問題を解決する

これらのタスクには、LATEX または自然言語で表現される問題が含まれます外部ツールを使用せずに、独立したテキストの回答を生成します。研究者が使用する評価ベンチマークには、MATH、GSM8k、OCWCourses、SAT、MMLU-STEM などがあります。

結果は以下の表 1 に示されています。Proof-Pile-2 コーパスに対する LLEMMA の継続的な事前トレーニングにより、5 つの数学的ベンチマークにおける少数サンプルのパフォーマンスが向上しました。その中で、LLEMMA 34B は向上しました。 GSM8k では、MATH では Code Llama より 20 パーセント ポイント高く、MATH では Code Llama より 13 パーセント ポイント高くなります。同時に、LLEMMA 7B は独自の Minerva モデルを上回りました。

したがって、研究者らは、Proof-Pile-2 での継続的な事前トレーニングが、事前トレーニングされたモデルの数学的問題を解決する能力の向上に役立つ可能性があると結論付けました。

#ツールを使用して数学の問題を解決する

これらのタスクには、問題を解決するための計算ツールの使用が含まれます。研究者が使用する評価ベンチマークには、MATH Python や GSM8k Python などがあります。

結果を以下の表 3 に示します。LLEMMA は両方のタスクで Code Llama よりも優れています。両方のツールを使用した場合の MATH および GSM8k のパフォーマンスも、ツールを使用しない場合よりも優れています。

形式数学

Proof-Pile-2 の AlgebraicStack データセットには、Lean と Isabelle から抽出された形式的な証明を含む、形式的な数学データの 15 億トークンが保持されています。形式数学の完全な研究はこの記事の範囲を超えていますが、次の 2 つのタスクで LLEMMA の数ショットのパフォーマンスを評価します。

非公式証明タスクから公式証明タスクへ、つまり、公式命題、非公式 LATEX 命題、および非公式 LATEX が与えられた場合証明 この場合、形式的な証明を生成します;

形式間の証明タスクは、一連の証明ステップ (または戦略) を生成することによって形式的な命題を証明することです。

結果は以下の表 4 に示されており、LLEMMA の Proof-Pile-2 での継続的な事前トレーニングにより、2 つの形式的定理証明タスクにおける少数サンプルのパフォーマンスが向上しました。

データ混合の影響

言語モデルをトレーニングするときの一般的なアプローチは、データの高品質のサブセットがアップサンプリングされます。研究者らは、慎重に選択したいくつかのブレンド ウェイトに対して短いトレーニングを実行することで、ブレンド ウェイトを選択しました。次に、高品質の提示されたテキストのセット (ここでは MATH トレーニング セットが使用されました) の混乱を最小限に抑える混合重みが選択されました。

以下の表 5 は、arXiv、Web、コードなどのさまざまなデータ混合でトレーニングした後のモデルの MATH トレーニング セットの複雑さを示しています。

#技術的な詳細と評価結果については、原著論文を参照してください。

以上がパラメータがほぼ半分であるため、パフォーマンスは Google Minerva に近く、別の大規模な数学モデルはオープンソースですの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。