テレンス・タオのクレイジー・アムウェイ副操縦士: 1 ページの校正を完了するのに役立ち、その後のプロセスを推測することもできました
GPT-4 によって「承認」された後、副操縦士はテレンス・タオによって待ち伏せ攻撃も受けました。
彼は、プログラミング時に、Copilot は次に何をするかを直接予測できると率直に言いました。
Copilot を使用すると、研究がより便利になり、Tao Zhexuan もそれを使用して、最新の研究結果を完成させるのに役立ちました。

Tao Zhexuan 氏は、論文のこの部分は実際には 1 ページしかない、と述べました。
しかし、この 1 ページの証明を完成させるために、彼は新しく学んだプログラミング言語 Lean4 を使用して 200 行を超えるコードを書きました。

Tao Zhexuan の公開コードの GitHub ページでは、Copilot によってコードの記述速度が半分以上向上したことがわかります。
Tao Zhexuan 氏は、Lean4 を選択した理由は、長い式の対象を絞った部分置換を実行する「書き換え戦略」のためであると述べました。
たとえば、複素関数 f(x) が定義されている場合、f(114514) の式を入力したい場合、コードを使用して x を 114514 に直接「書き換え」ることができます。
Tao Zhexuan 氏は、この機能は数式を繰り返し入力する必要がある LaTeX に比べてあまり便利ではないと述べています。
それでは、Tao Zhexuan の「1 ページの証拠」は今回、どのような新しい結果を私たちにもたらしたのでしょうか?
新たな不等式の 1 ページの証明
この論文では、マクラフリンの不等式に関連する問題について説明します。
マクラフリンの不等式は、数学における古典的な不等式です。「非負の実数の算術平均は幾何平均以上である」という法則に基づいて導出されます。次のように表現できます。
y1…yn が非負の実数であると仮定します。k=1…n の場合、平均 Sk は次のようになります。 (分母が分子である項の数) として定義されます:
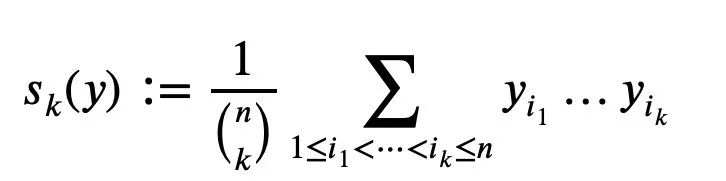
#これは、根を持つ n 次の多項式の正規化された係数として発生します。
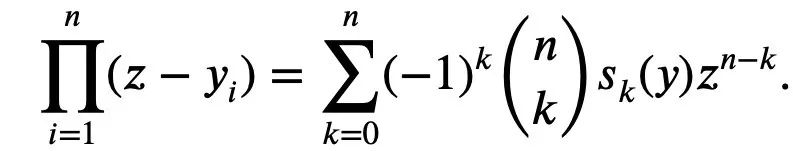
(この式を覚えておいてください。これを式 1 と呼びます)
次に、マクラフリンの不等式は次のように表すことができます:
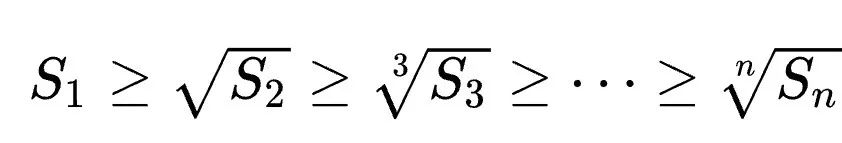
このうち、等号は、すべての yi が等しい場合にのみ当てはまります。
微積分には、古典的なニュートンの不等式もあります。
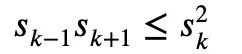
任意の 1≤k
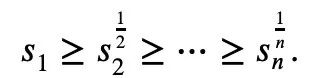
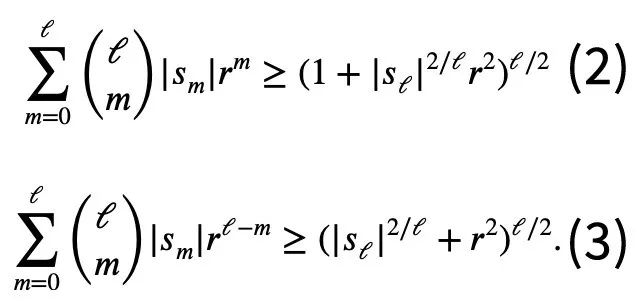
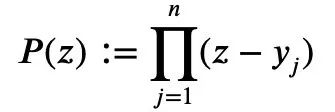
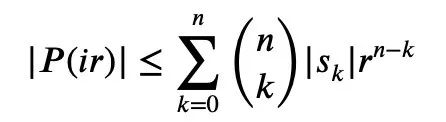
したがって、必要なのは下限を設定することだけです。
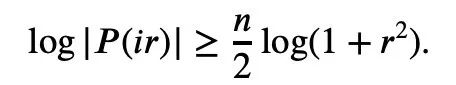
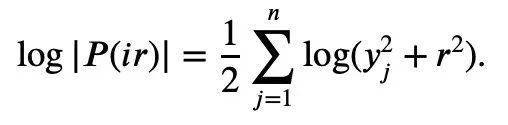
t a) は凸であり、a>0 であるため、次の不等式が得られます。
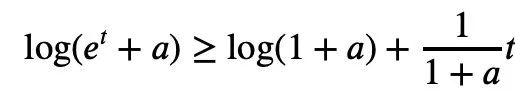 # a=r
# a=r
、t=2log yj の場合、次のように結論付けることができます:
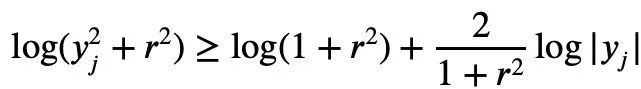 上記はテレンス タオ プロセスによる証明ですが、正規化された |S
上記はテレンス タオ プロセスによる証明ですが、正規化された |S
|=1 の場合、次の式が成り立ちます。ステップ: 洗練されたバージョンを作成する今回言及した「1 ページの証明」に加えて、Tao Zhexuan の論文では、別の新しい定理も提案されています。つまり、任意の 1 ≤ k ≤ ℓ≤ n についてです。:
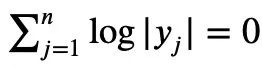
テレンス・タオ氏はブログ投稿で、次のステップはこの不等式の洗練されたバージョンを提案することであると明らかにしました。
Tao Zhexuan氏は、証明のプロセスは「練習と同じように」非常に簡単で、微積分を使って行うことができると述べた。
ただし、議論のこの部分では漸近記号が使用されているため、多少の困難があるとも彼は述べました。 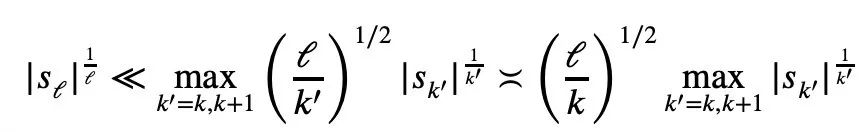
新しい結論がどのようなものになるかを待ってみましょう。
One More Thing
Tao Zhexuan は AI ツールの熱心なファンであり、Copilot、GPT-4、およびその他の補助ツールを推奨しています。 

以上がテレンス・タオのクレイジー・アムウェイ副操縦士: 1 ページの校正を完了するのに役立ち、その後のプロセスを推測することもできましたの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7467
7467
 15
15
 1376
1376
 52
52
 77
77
 11
11
 19
19
 20
20
 Laravelの地理空間:インタラクティブマップと大量のデータの最適化
Apr 08, 2025 pm 12:24 PM
Laravelの地理空間:インタラクティブマップと大量のデータの最適化
Apr 08, 2025 pm 12:24 PM
700万のレコードを効率的に処理し、地理空間技術を使用したインタラクティブマップを作成します。この記事では、LaravelとMySQLを使用して700万を超えるレコードを効率的に処理し、それらをインタラクティブなマップの視覚化に変換する方法について説明します。最初の課題プロジェクトの要件:MySQLデータベースに700万のレコードを使用して貴重な洞察を抽出します。多くの人は最初に言語をプログラミングすることを検討しますが、データベース自体を無視します。ニーズを満たすことができますか?データ移行または構造調整は必要ですか? MySQLはこのような大きなデータ負荷に耐えることができますか?予備分析:キーフィルターとプロパティを特定する必要があります。分析後、ソリューションに関連している属性はわずかであることがわかりました。フィルターの実現可能性を確認し、検索を最適化するためにいくつかの制限を設定しました。都市に基づくマップ検索
 MySQLを解決する方法は開始できません
Apr 08, 2025 pm 02:21 PM
MySQLを解決する方法は開始できません
Apr 08, 2025 pm 02:21 PM
MySQLの起動が失敗する理由はたくさんあり、エラーログをチェックすることで診断できます。一般的な原因には、ポートの競合(ポート占有率をチェックして構成の変更)、許可の問題(ユーザー許可を実行するサービスを確認)、構成ファイルエラー(パラメーター設定のチェック)、データディレクトリの破損(テーブルスペースの復元)、INNODBテーブルスペースの問題(IBDATA1ファイルのチェック)、プラグインロード障害(エラーログのチェック)が含まれます。問題を解決するときは、エラーログに基づいてそれらを分析し、問題の根本原因を見つけ、問題を防ぐために定期的にデータをバックアップする習慣を開発する必要があります。
 リモートシニアバックエンジニア(プラットフォーム)がサークルが必要です
Apr 08, 2025 pm 12:27 PM
リモートシニアバックエンジニア(プラットフォーム)がサークルが必要です
Apr 08, 2025 pm 12:27 PM
リモートシニアバックエンジニアの求人事業者:サークル場所:リモートオフィスジョブタイプ:フルタイム給与:$ 130,000- $ 140,000職務記述書サークルモバイルアプリケーションとパブリックAPI関連機能の研究開発に参加します。ソフトウェア開発ライフサイクル全体をカバーします。主な責任は、RubyonRailsに基づいて独立して開発作業を完了し、React/Redux/Relay Front-Endチームと協力しています。 Webアプリケーションのコア機能と改善を構築し、機能設計プロセス全体でデザイナーとリーダーシップと緊密に連携します。肯定的な開発プロセスを促進し、反復速度を優先します。 6年以上の複雑なWebアプリケーションバックエンドが必要です
 mysqlはjsonを返すことができますか
Apr 08, 2025 pm 03:09 PM
mysqlはjsonを返すことができますか
Apr 08, 2025 pm 03:09 PM
MySQLはJSONデータを返すことができます。 json_extract関数はフィールド値を抽出します。複雑なクエリについては、Where句を使用してJSONデータをフィルタリングすることを検討できますが、そのパフォーマンスへの影響に注意してください。 JSONに対するMySQLのサポートは絶えず増加しており、最新バージョンと機能に注意を払うことをお勧めします。
 酸性特性を理解する:信頼できるデータベースの柱
Apr 08, 2025 pm 06:33 PM
酸性特性を理解する:信頼できるデータベースの柱
Apr 08, 2025 pm 06:33 PM
データベース酸属性の詳細な説明酸属性は、データベーストランザクションの信頼性と一貫性を確保するための一連のルールです。データベースシステムがトランザクションを処理する方法を定義し、システムのクラッシュ、停電、または複数のユーザーの同時アクセスの場合でも、データの整合性と精度を確保します。酸属性の概要原子性:トランザクションは不可分な単位と見なされます。どの部分も失敗し、トランザクション全体がロールバックされ、データベースは変更を保持しません。たとえば、銀行の譲渡が1つのアカウントから控除されているが別のアカウントに増加しない場合、操作全体が取り消されます。 TRANSACTION; updateaccountssetbalance = balance-100wh
 MySQLの主な鍵はヌルにすることができます
Apr 08, 2025 pm 03:03 PM
MySQLの主な鍵はヌルにすることができます
Apr 08, 2025 pm 03:03 PM
MySQLプライマリキーは、データベース内の各行を一意に識別するキー属性であるため、空にすることはできません。主キーが空になる可能性がある場合、レコードを一意に識別することはできません。これにより、データの混乱が発生します。一次キーとして自己挿入整数列またはUUIDを使用する場合、効率やスペース占有などの要因を考慮し、適切なソリューションを選択する必要があります。
 マスターSQL制限条項:クエリの行数を制御する
Apr 08, 2025 pm 07:00 PM
マスターSQL制限条項:クエリの行数を制御する
Apr 08, 2025 pm 07:00 PM
sqllimit句:クエリ結果の行数を制御します。 SQLの制限条項は、クエリによって返される行数を制限するために使用されます。これは、大規模なデータセット、パジネートされたディスプレイ、テストデータを処理する場合に非常に便利であり、クエリ効率を効果的に改善することができます。構文の基本的な構文:SelectColumn1、column2、... FromTable_nameLimitnumber_of_rows; number_of_rows:返された行の数を指定します。オフセットの構文:SelectColumn1、column2、... FromTable_nameLimitoffset、number_of_rows; offset:skip
 バングラ部分モデル検索のlaravelEloquent orm)
Apr 08, 2025 pm 02:06 PM
バングラ部分モデル検索のlaravelEloquent orm)
Apr 08, 2025 pm 02:06 PM
LaravelEloquentモデルの検索:データベースデータを簡単に取得するEloquentormは、データベースを操作するための簡潔で理解しやすい方法を提供します。この記事では、さまざまな雄弁なモデル検索手法を詳細に紹介して、データベースからのデータを効率的に取得するのに役立ちます。 1.すべてのレコードを取得します。 ALL()メソッドを使用して、データベーステーブルですべてのレコードを取得します:useapp \ models \ post; $ post = post :: all();これにより、コレクションが返されます。 Foreach Loopまたはその他の収集方法を使用してデータにアクセスできます。




