4 ビット浮動小数点量子化をサポートする最初の LLM は、LLaMA、BERT などの展開上の問題を解決するために登場しました。
大規模言語モデル (LLM) 圧縮は常に多くの注目を集めています。トレーニング後の量子化は、一般的に使用されるアルゴリズムの 1 つです。ただし、既存の PTQ メソッドのほとんどは整数量子化であり、ビット数が以下の場合は8 では、量子化モデルの精度が大幅に低下します。整数 (INT) 量子化と比較して、浮動小数点 (FP) 量子化はロングテール分布をより適切に表現できるため、FP 量子化をサポートするハードウェア プラットフォームが増えています。この記事では、大規模モデルの FP 定量化のソリューションを提供します。 EMNLP 2023 で公開された記事。

- 文書アドレス: https://arxiv.org/abs/2310.16836
- コード アドレス: https://github.com/nbasyl/LLM-FP4
この記事を理解するには、まず次のことを行う必要があります。浮動小数点形式と浮動小数点量子化に関する基本的な知識があること、まず、浮動小数点数は次の式で表すことができます:

s は符号ビットを表し、m は仮数ビットを表し、e は指数ビットを表します。 p は 0 から 2^e - 1 までの値で、現在の数値をどの指数区間に分割するかを示すために使用されます。d は 0 または 1 の値をとり、i 番目の仮数ビットを示すために使用されます。 b はバイアスで、指数間隔を調整するために使用される整数値です。
#次のセクションでは、浮動小数点定量化がどのように機能するかを説明します。まず、入力値は「スケールとクリップ」と呼ばれるステップを通過する必要があります。このステップでは、まず入力値を浮動小数点数が表現できる最大範囲 (±Qmax) にクリップします。具体的な計算式は次のとおりです。#整数量子化と同様に、FP 量子化でも、入力を適切な間隔にスケーリングするために完全精度のスケーリング係数が追加されることがわかります。行列乗算を計算する場合、スケーリング係数は低ビット行列乗算とは別に計算されるため、大きなオーバーヘッドは発生しません。この完全精度のスケーリング係数を組み込んだ後、さまざまな量子化テンソルを、それに応じてさまざまな最大値および最小値の間隔にクリップできます。実際の使用では、入力テンソルの値の範囲に基づいて必要な量子化間隔が決定され、式 (4) を使用して対応するバイアスが導出されます。式 (4) のバイアスは実際の値のスケーリング係数として使用できることに注意してください。式 (2)(3) を参照してください。
 #浮動小数点量子化の次のステップは、決定された量子化間隔の値を対応する量子化間隔に割り当てることです。このプロセスは比較と量子化と呼ばれます:
#浮動小数点量子化の次のステップは、決定された量子化間隔の値を対応する量子化間隔に割り当てることです。このプロセスは比較と量子化と呼ばれます:
##上図は量子化プロセスを直感的に示したもので、現在の入力値は式 5 と比較された後、異なる量子化間隔に量子化されます。
量子化されたアクティベーションと重みを取得した後、前述したように、ここでのスケーリング係数が最初に計算され、次の効率的な行列乗算が実現され、行列乗算の高速化が完了します。

##そして、この記事では、FP 量子化の精度が指数ビットと量子化間隔の設定に密接に関係していることを指摘しています。
以前の論文では、異なる FP フォーマット (つまり、浮動小数点数の指数ビット/仮数ビットの設定) 間で量子化誤差に大きな違いがあることが確認されています。適切な FP 形式が選択された場合にのみ、FP 量子化は INT 量子化よりも適切にロングテール分布を表現できます
この記事では、検索ベースの浮動小数点量子化アルゴリズムを使用して、浮動小数点数に最適な指数と仮数のビット設定、および対応する量子化間隔を包括的な検索方法で決定するソリューションを提案します。 さらに、さまざまなタイプの Transformer モデル (Bert、LLaMA、ViT) では、定量化の難しさに深刻な影響を与える別の現象があります。モデル それらの間の大きさの違いは非常に大きいですが、同じチャネル間の大きさの違いは非常に一貫しています。以前の研究 LLM.int8 と SmoothQuant でも同様の現象が見つかりましたが、この記事では、この現象は LLM にだけ存在するだけでなく、他の Transformer モデル (以下に示す LLaMA、BERT、および DeIT-S) にも同様の活性化分布が見つかったことを指摘しています。 図からわかるように、これらの異常に大きいチャネルは残りのチャネルよりもはるかに大きいため、活性化テンソルを定量化する過程で、量子化精度は主にこれらの外れ値によって決まり、それによって他のチャネル値の量子化範囲が抑制され、最終的には量子化精度に対する全体的な影響が軽減されます。これにより、特にビット数が特定のレベルに低下した場合に、量子化の最終結果が崩れる原因になります。以下の図に示すように、効率的な行列乗算中にスケーリング係数を抽出できるのはテンソル単位およびトークン単位の量子化のみであり、チャネル単位の量子化は効率的な行列乗算をサポートしていないことに注意してください。 #問題を解決し、効率的な行列乗算を維持するために、この論文では少量の修正されたデータ セットを使用します。各チャネルのアクティベーションの最大値を事前に計算し、スケーリング係数を計算します。次に、スケーリング係数は、各チャネルの 2 の累乗を乗算した各テンソルの実数に分割されます。この 2 のべき乗は、FP の指数偏差で表すことができます。プロセス全体は次の式で表すことができます。 さらに、キャリブレーションが完了した後、チャネルごとの指数バイアスは変化しなくなるため、重みの量子化とともに事前に計算して、このチャネルごとの指数バイアスを量子化された重みに統合して、量子化の精度を向上させることができます。完全なプロセスは次のとおりです。 プリオフセットの後、元のアクティベーション関数の各チャネルの完全精度オフセットを観察できます。位置はテンソルベースの実数スケーリング係数になり、分解された整数オフセットが重み内の元の整数オフセットの位置に移動されます。詳細については、式 4 を参照してください。 (事前にシフトされた指数バイアス) を使用すると、効率的な行列乗算の原理を維持しながら、量子化精度をより向上させることができます。この方法を直感的に表示すると、次の図のようになります。 #最後に、この記事では浮動小数点量子化 (FPQ) 手法について説明します。LLaMA、BERT、および ViTs モデルでは、4 ビット量子化が SOTA をはるかに超える結果を達成しました。特に、この記事では、4 ビット量子化 LLaMA-13B モデルがゼロショット推論タスクで 63.1 の平均スコアを達成していることを示しています。これは、完全精度モデルよりも 5.8 ポイント低いだけであり、以前のモデルよりも高い平滑化量を持っています。 SOTA メソッド 12.7 は、現在知られている数少ない実現可能な 4 ビット量子化スキームの 1 つです。  #
#




以上が4 ビット浮動小数点量子化をサポートする最初の LLM は、LLaMA、BERT などの展開上の問題を解決するために登場しました。の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7562
7562
 15
15
 1384
1384
 52
52
 84
84
 11
11
 28
28
 98
98
 世界で最も強力なオープンソース MoE モデルが登場。GPT-4 に匹敵する中国語機能を備え、価格は GPT-4-Turbo のわずか 1% 近くです
May 07, 2024 pm 04:13 PM
世界で最も強力なオープンソース MoE モデルが登場。GPT-4 に匹敵する中国語機能を備え、価格は GPT-4-Turbo のわずか 1% 近くです
May 07, 2024 pm 04:13 PM
従来のコンピューティングを超える能力を備えているだけでなく、より低コストでより効率的なパフォーマンスを実現する人工知能モデルを想像してみてください。これは SF ではありません。世界で最も強力なオープンソース MoE モデルである DeepSeek-V2[1] が登場しました。 DeepSeek-V2 は、経済的なトレーニングと効率的な推論の特徴を備えた強力な専門家混合 (MoE) 言語モデルです。これは 236B のパラメータで構成されており、そのうち 21B は各マーカーをアクティブにするために使用されます。 DeepSeek67B と比較して、DeepSeek-V2 はパフォーマンスが優れていると同時に、トレーニング コストを 42.5% 節約し、KV キャッシュを 93.3% 削減し、最大生成スループットを 5.76 倍に高めます。 DeepSeek は一般的な人工知能を研究する会社です
 AI が数学研究を破壊する!フィールズ賞受賞者で中国系アメリカ人の数学者が上位 11 件の論文を主導 | テレンス・タオが「いいね!」しました
Apr 09, 2024 am 11:52 AM
AI が数学研究を破壊する!フィールズ賞受賞者で中国系アメリカ人の数学者が上位 11 件の論文を主導 | テレンス・タオが「いいね!」しました
Apr 09, 2024 am 11:52 AM
AI は確かに数学を変えつつあります。最近、この問題に細心の注意を払っている陶哲軒氏が『米国数学協会会報』(米国数学協会会報)の最新号を送ってくれた。 「機械は数学を変えるのか?」というテーマを中心に、多くの数学者が意見を述べ、そのプロセス全体は火花に満ち、ハードコアで刺激的でした。著者には、フィールズ賞受賞者のアクシャイ・ベンカテシュ氏、中国の数学者鄭楽軍氏、ニューヨーク大学のコンピューター科学者アーネスト・デイビス氏、その他業界で著名な学者を含む強力な顔ぶれが揃っている。 AI の世界は劇的に変化しています。これらの記事の多くは 1 年前に投稿されたものです。
 Google は大喜び: JAX のパフォーマンスが Pytorch や TensorFlow を上回りました! GPU 推論トレーニングの最速の選択肢となる可能性があります
Apr 01, 2024 pm 07:46 PM
Google は大喜び: JAX のパフォーマンスが Pytorch や TensorFlow を上回りました! GPU 推論トレーニングの最速の選択肢となる可能性があります
Apr 01, 2024 pm 07:46 PM
Google が推進する JAX のパフォーマンスは、最近のベンチマーク テストで Pytorch や TensorFlow のパフォーマンスを上回り、7 つの指標で 1 位にランクされました。また、テストは最高の JAX パフォーマンスを備えた TPU では行われませんでした。ただし、開発者の間では、依然として Tensorflow よりも Pytorch の方が人気があります。しかし、将来的には、おそらくより大規模なモデルが JAX プラットフォームに基づいてトレーニングされ、実行されるようになるでしょう。モデル 最近、Keras チームは、ネイティブ PyTorch 実装を使用して 3 つのバックエンド (TensorFlow、JAX、PyTorch) をベンチマークし、TensorFlow を使用して Keras2 をベンチマークしました。まず、主流のセットを選択します
 こんにちは、電気アトラスです!ボストン・ダイナミクスのロボットが復活、180度の奇妙な動きにマスク氏も恐怖
Apr 18, 2024 pm 07:58 PM
こんにちは、電気アトラスです!ボストン・ダイナミクスのロボットが復活、180度の奇妙な動きにマスク氏も恐怖
Apr 18, 2024 pm 07:58 PM
Boston Dynamics Atlas は正式に電動ロボットの時代に突入します!昨日、油圧式アトラスが歴史の舞台から「涙ながらに」撤退したばかりですが、今日、ボストン・ダイナミクスは電動式アトラスが稼働することを発表しました。ボストン・ダイナミクス社は商用人型ロボットの分野でテスラ社と競争する決意を持っているようだ。新しいビデオが公開されてから、わずか 10 時間ですでに 100 万人以上が視聴しました。古い人が去り、新しい役割が現れるのは歴史的な必然です。今年が人型ロボットの爆発的な年であることは間違いありません。ネットユーザーは「ロボットの進歩により、今年の開会式は人間のように見え、人間よりもはるかに自由度が高い。しかし、これは本当にホラー映画ではないのか?」とコメントした。ビデオの冒頭では、アトラスは仰向けに見えるように地面に静かに横たわっています。次に続くのは驚くべきことです
 MLP に代わる KAN は、オープンソース プロジェクトによって畳み込みまで拡張されました
Jun 01, 2024 pm 10:03 PM
MLP に代わる KAN は、オープンソース プロジェクトによって畳み込みまで拡張されました
Jun 01, 2024 pm 10:03 PM
今月初め、MIT やその他の機関の研究者らは、MLP に代わる非常に有望な代替案である KAN を提案しました。 KAN は、精度と解釈可能性の点で MLP よりも優れています。また、非常に少数のパラメーターを使用して、多数のパラメーターを使用して実行する MLP よりも優れたパフォーマンスを発揮できます。たとえば、著者らは、KAN を使用して、より小規模なネットワークと高度な自動化で DeepMind の結果を再現したと述べています。具体的には、DeepMind の MLP には約 300,000 個のパラメーターがありますが、KAN には約 200 個のパラメーターしかありません。 KAN は、MLP が普遍近似定理に基づいているのに対し、KAN はコルモゴロフ-アーノルド表現定理に基づいているのと同様に、強力な数学的基礎を持っています。以下の図に示すように、KAN は
 テスラのロボットは工場で働く、マスク氏:手の自由度は今年22に達する!
May 06, 2024 pm 04:13 PM
テスラのロボットは工場で働く、マスク氏:手の自由度は今年22に達する!
May 06, 2024 pm 04:13 PM
テスラのロボット「オプティマス」の最新映像が公開され、すでに工場内で稼働可能となっている。通常の速度では、バッテリー(テスラの4680バッテリー)を次のように分類します:公式は、20倍の速度でどのように見えるかも公開しました - 小さな「ワークステーション」上で、ピッキング、ピッキング、ピッキング:今回は、それがリリースされたハイライトの1つビデオの内容は、オプティマスが工場内でこの作業を完全に自律的に行い、プロセス全体を通じて人間の介入なしに完了するというものです。そして、オプティマスの観点から見ると、自動エラー修正に重点を置いて、曲がったバッテリーを拾い上げたり配置したりすることもできます。オプティマスのハンドについては、NVIDIA の科学者ジム ファン氏が高く評価しました。オプティマスのハンドは、世界の 5 本指ロボットの 1 つです。最も器用。その手は触覚だけではありません
 FisheyeDetNet: 魚眼カメラに基づいた最初のターゲット検出アルゴリズム
Apr 26, 2024 am 11:37 AM
FisheyeDetNet: 魚眼カメラに基づいた最初のターゲット検出アルゴリズム
Apr 26, 2024 am 11:37 AM
目標検出は自動運転システムにおいて比較的成熟した問題であり、その中でも歩行者検出は最も初期に導入されたアルゴリズムの 1 つです。ほとんどの論文では非常に包括的な研究が行われています。ただし、サラウンドビューに魚眼カメラを使用した距離認識については、あまり研究されていません。放射状の歪みが大きいため、標準のバウンディング ボックス表現を魚眼カメラに実装するのは困難です。上記の説明を軽減するために、拡張バウンディング ボックス、楕円、および一般的な多角形の設計を極/角度表現に探索し、これらの表現を分析するためのインスタンス セグメンテーション mIOU メトリックを定義します。提案された多角形モデルの FisheyeDetNet は、他のモデルよりも優れたパフォーマンスを示し、同時に自動運転用の Valeo 魚眼カメラ データセットで 49.5% の mAP を達成しました。
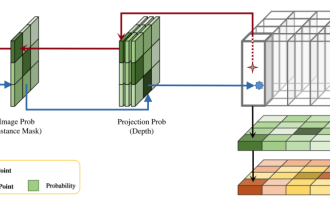 DualBEV: BEVFormer および BEVDet4D を大幅に上回る、本を開いてください!
Mar 21, 2024 pm 05:21 PM
DualBEV: BEVFormer および BEVDet4D を大幅に上回る、本を開いてください!
Mar 21, 2024 pm 05:21 PM
この論文では、自動運転においてさまざまな視野角 (遠近法や鳥瞰図など) から物体を正確に検出するという問題、特に、特徴を遠近法 (PV) 空間から鳥瞰図 (BEV) 空間に効果的に変換する方法について検討します。 Visual Transformation (VT) モジュールを介して実装されます。既存の手法は、2D から 3D への変換と 3D から 2D への変換という 2 つの戦略に大別されます。 2D から 3D への手法は、深さの確率を予測することで高密度の 2D フィーチャを改善しますが、特に遠方の領域では、深さ予測に固有の不確実性により不正確さが生じる可能性があります。 3D から 2D への方法では通常、3D クエリを使用して 2D フィーチャをサンプリングし、Transformer を通じて 3D と 2D フィーチャ間の対応のアテンション ウェイトを学習します。これにより、計算時間と展開時間が増加します。




