人工知能の歴史とマトリックスを探る: 人工知能チュートリアル (2)

このシリーズの最初の記事では、人工知能、機械学習、深層学習、データ サイエンスなどの分野のつながりと違いについて説明しました。また、シリーズ全体で使用するプログラミング言語やツールなどについても、いくつかの難しい選択をしました。最後に、行列の知識も少し紹介しました。この記事では、人工知能の中核であるマトリックスについて詳しく説明します。その前に、まず人工知能の歴史を理解しましょう

なぜ人工知能の歴史を理解する必要があるのでしょうか?歴史上何度もAIブームはありましたが、多くの場合、AIの可能性に対する大きな期待は実現しませんでした。人工知能の歴史を理解すると、この人工知能の波が奇跡を起こすのか、それともはじけようとしている単なるバブルなのかを知ることができます。

人工知能の起源についての理解が始まったのはいつですか?デジタルコンピュータが発明されてからでしょうか？それとももっと前に？全知の存在の追求は文明の始まりにまで遡ると私は信じています。たとえば、古代ギリシャ神話のデルフィは、どんな質問にも答えることができる預言者でした。人間の知性を超えた創造的な機械の探求も、古くから私たちを魅了してきました。歴史上、チェスマシンを構築する試みは何度か失敗してきました。その中には、本物のロボットではなく、内部に隠されたチェスプレイヤーによって制御される悪名高いメカタークも含まれます。ジョン ネイピアによって発明された対数、ブレーズ パスカルの計算機、チャールズ バベッジの分析エンジンはすべて、人工知能の開発において重要な役割を果たしました

それでは、これまでの人工知能の開発のマイルストーンは何でしょうか?前述したように、デジタル コンピューターの発明は、人工知能研究の歴史の中で最も重要な出来事です。スケーラビリティが電力要件に依存する電気機械デバイスとは異なり、デジタル デバイスは、真空管からトランジスタ、集積回路、そして現在は VLSI に至るまで、技術の進歩の恩恵を受けています。

人工知能の開発におけるもう 1 つの重要なマイルストーンは、アラン チューリングによる人工知能の最初の理論分析です。彼は有名なチューリング テストを提案しました。

1950 年代後半、ジョン マッカーシー

1970 年代から 1980 年代までには、アルゴリズムがこの時期に大きな役割を果たしました。この間、多くの新しい効率的なアルゴリズムが提案されました。 1960年代後半、ドナルド・クヌース（彼を知ることを強くお勧めします。コンピュータサイエンスの世界では、数学の世界ではガウスやオイラーに相当します）は、有名な「The Art of Computer Programming」の第1巻を出版しました。プログラミングの進歩は、アルゴリズム時代の始まりを示しました。この数年間で、多くの汎用アルゴリズムやグラフ アルゴリズムが開発されました。さらに、人工ニューラルネットワークに基づくプログラミングもこの時期に登場しました。 1940 年代には、ウォーレン S. マカロックとウォルター ピッツ

人工知能には、デジタル時代において少なくとも 2 つの有望な機会があったにもかかわらず、どちらの機会も期待を下回りました。現在の人工知能の波もこれに似たものなのでしょうか？この質問には答えるのが難しいです。ただし、今回は人工知能の影響が大きいと個人的には考えています（LCTT翻訳注釈：この記事は2022年6月に公開され、ChatGTPはその半年後に発売されました）。なぜそのような予測ができるのでしょうか？まず、高性能コンピューティング機器が安価で容易に入手できるようになりました。 1960 年代や 1980 年代には、このような強力なコンピューティング デバイスは数台しかありませんでしたが、現在では数百万台、さらには数十億台も存在します。第二に、人工知能や機械学習プログラムのトレーニングに利用できる膨大な量のデータが存在します。 1990 年代にデジタル画像処理に従事していたデジタル画像エンジニアがアルゴリズムのトレーニングに何人のデジタル画像を使用できたか想像してみてください。おそらく数千、数万でしょう。現在、データ サイエンス プラットフォームの Kaggle (Google の子会社) だけでも 10,000 を超えるデータ セットがあります。インターネットによって毎日生成される膨大な量のデータにより、アルゴリズムのトレーニングが容易になります。第三に、高速インターネット接続により、大規模な機関との連携が容易になります。 21 世紀の最初の 10 年間、コンピューター科学者間の協力は困難でした。しかし、インターネットの速度のおかげで、Google Colab、Kaggle、Project Jupiter などの人工知能プロジェクトとのコラボレーションが現実になりました。これら 3 つの要素に基づいて、私は人工知能が今後も永遠に存在し、多くの優れたアプリケーションが登場すると信じています

行列の知識をもっと見る

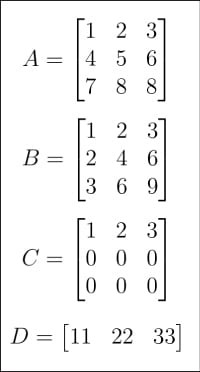図 1: 行列 A 、B、C、D

人工知能の歴史を理解したら、今度は行列とベクトルの話題に戻ります。以前の記事でも簡単に紹介しました。今回は『マトリックス』の世界を深く掘り下げていきます。まず、図 1 と図 2 をご覧ください。A から H までの合計 8 つの行列が示されています。人工知能と機械学習のチュートリアルではなぜこれほど多くの行列が必要なのでしょうか?まず、前述したように、行列は線形代数の中核であり、線形代数は機械学習の頭脳ではありませんが、機械学習の中核です。次に、以下の説明では、各行列には特定の目的があります。

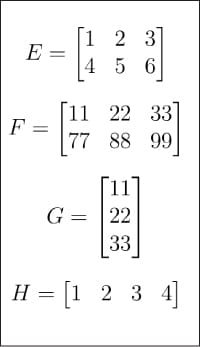図 2: 行列 E、F、G、H

その方法を見てみましょう。行列が表現され、その詳細を取得する方法。図 3 は、NumPy を使用して行列 A を表現する方法を示しています。行列と配列はまったく同じではありませんが、実際のアプリケーションではこれらを同義語として使用することがよくあります

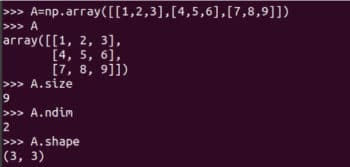図 3: NumPy での行列 A の表現

I は強力ですNumPy の array 関数を使用して行列を作成する方法を注意深く学習することをお勧めします。 NumPy は、2 次元の配列と行列を作成する matrix 関数も提供します。ただし、将来的には非推奨になるため、使用は推奨されません。行列 A の一部の詳細も図 3 に示します。 A.size は、配列内の要素の数を示します。私たちの場合は9です。コード A.nidm は配列の次元を表します。行列 A が 2 次元であることは簡単にわかります。 A.shape は行列 A の次数を表します。行列の次数は行列の行数と列数です。これ以上は説明しませんが、NumPy ライブラリを使用するときは、行列のサイズ、次元、順序に注意する必要があります。図 4 は、行列のサイズ、次元、順序を慎重に特定する必要がある理由を示しています。配列の定義方法にわずかな違いがあると、そのサイズ、次元数、順序に違いが生じる可能性があります。したがって、プログラマは行列を定義する際にこれらの詳細に特別な注意を払う必要があります。

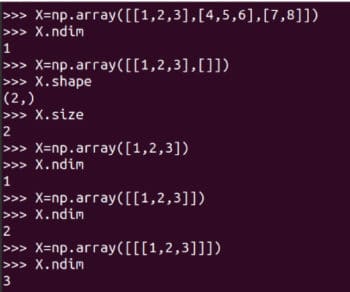図 4: 配列のサイズ、次元、順序

次に、基本的な行列演算をいくつか実行してみましょう。図 5 は、行列 A と B がどのように加算されるかを示しています。 NumPy は、行列を追加するための 2 つのメソッド、add 関数と 演算子を提供します。同じ次数の行列のみを追加できることに注意してください。たとえば、4 × 3 行列を 2 つ加算することはできますが、3 × 4 行列と 2 × 3 行列を加算することはできません。ただし、プログラミングは数学とは異なるため、NumPy は実際にはこの規則に従いません。図 5 には、行列 A と D を加算する様子も示されています。この種の行列の加算は数学的に違法であることに注意してください。 1 つはブロードキャストブロードキャストと呼ばれます

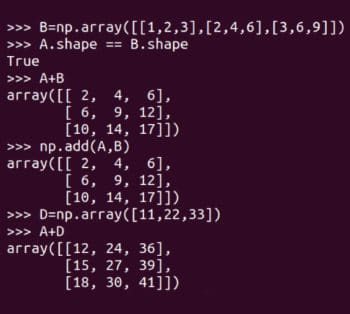再式: 図 5: 行列の合計

再式: 図 5: 行列の合計

A.shape == B.shape

ブロードキャスト機構は全能ではないため、行列DとHを追加しようとすると演算エラーが発生します。

当然除了矩阵加法外还有其它矩阵运算。图 6 展示了矩阵减法和矩阵乘法。它们同样有两种形式，矩阵减法可以由 subtract 函数或减法运算符 - 来实现，矩阵乘法可以由 matmul 函数或矩阵乘法运算符 @ 来实现。图 6 还展示了 逐元素乘法element-wise multiplication 运算符 * 的使用。请注意，只有 NumPy 的 matmul 函数和 @ 运算符执行的是数学意义上的矩阵乘法。在处理矩阵时要小心使用 * 运算符。

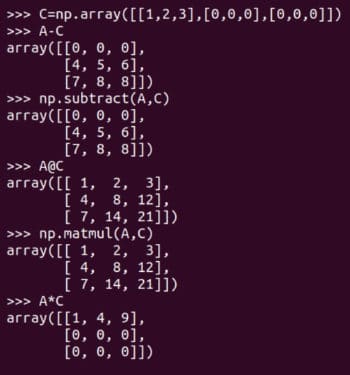图 6：更多矩阵运算

对于一个 m x n 阶和一个 p x q 阶的矩阵，当且仅当 n 等于 p 时它们才可以相乘，相乘的结果是一个 m x q 阶矩的阵。图 7 显示了更多矩阵相乘的示例。注意 E@A 是可行的，而 A@E 会导致错误。请仔细阅读对比 D@G 和 G@D 的示例。使用 shape 属性，确定这 8 个矩阵中哪些可以相乘。虽然根据严格的数学定义，矩阵是二维的，但我们将要处理更高维的数组。作为例子，下面的代码创建一个名为 T 的三维数组。

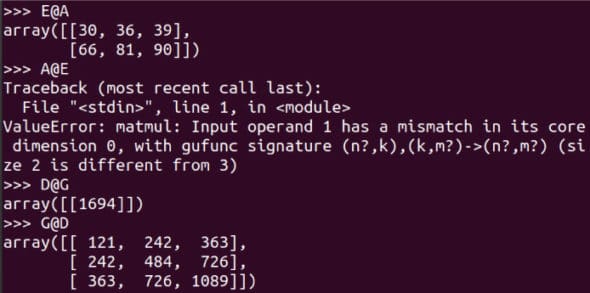图 7：更多矩阵乘法的例子

T = np.array([[[11,22], [33,44]], [[55,66], [77,88]]])

Pandas

到目前为止，我们都是通过键盘输入矩阵的。如果我们需要从文件或数据集中读取大型矩阵并处理，那该怎么办呢？这时我们就要用到另一个强大的 Python 库了——Pandas。我们以读取一个小的 CSV （逗号分隔值comma-separated value）文件为例。图 8 展示了如何读取 cricket.csv 文件，并将其中的前三行打印到终端上。在本系列的后续文章中将会介绍 Pandas 的更多特性。

图 8：用 Pandas 读取 CSV 文件

图 8：用 Pandas 读取 CSV 文件

矩阵的秩

需要进行改写的内容是：矩阵的秩

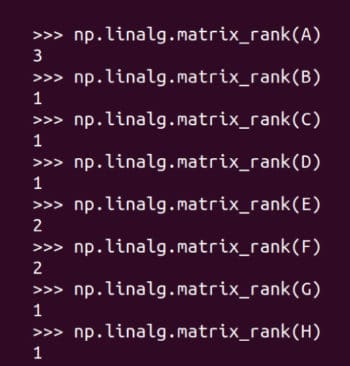図 9: 行列のランクの確認

これでこのコンテンツは終了です。次の記事では、ツールのライブラリを拡張して、人工知能および機械学習プログラムの開発に使用できるようにします。ニューラル ネットワーク、教師あり学習、教師なし学習についても詳しく説明します

以上が人工知能の歴史とマトリックスを探る: 人工知能チュートリアル (2)の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。