国立科学技術大学と第一師範大学の協力の概要: 「ホワイト ボックス」テンソル ネットワークが量子機械学習の解釈可能性と効率をどのように改善できるかを明らかにする

編集者|Ziluo

深層機械学習は AI のさまざまな分野で目覚ましい成功を収めていますが、高い解釈可能性と効率性を同時に達成することは依然として深刻です。課題

テンソル ネットワーク、つまり Tensor Network (TN) は、量子力学に由来し、成熟した数学ツールです。効率的な「ホワイト ボックス」機械学習ソリューションの開発において独自の利点を実証しました。

最近、首都師範大学の Ran Shiju 氏と中国科学院大学の Su Gang 氏は、量子力学からインスピレーションを得て、革新的なアプローチを検討しました。 TN に基づくこの手法は、深層機械学習における解釈可能性と効率性を両立させるという長年の課題に対する有望なソリューションを提供します。

一方で、TN ML の解釈可能性は、量子情報と多体物理学に基づく強固な理論的基盤によって実現できます。一方で、量子多体物理学で開発された強力な TN 表現と高度なコンピューティング技術により、高い効率を実現できます。量子コンピューターの急速な発展に伴い、TN は近い将来、「量子 AI」の方向で量子ハードウェア上で実行できる新しいソリューションを生み出すことが期待されています

このレビューは「Tensor Networks」に基づいています。 for Interpretable および「Efficient Quantum-Inspired Machine Learning」は、2023 年 11 月 17 日に「Intelligent Computing」で公開されました。

論文リンク: https://spj.science.org/doi/10.34133/icomputing.0061

深層学習モデル、特にニューラル ネットワーク モデルは、意思決定プロセスが複雑で説明が難しいため、「ブラック ボックス」と呼ばれることがあります。ニューラル ネットワークは現在、最も強力な深層学習モデルです。そのパワーの代表的な例は GPT です。しかし、GPT であっても、説明可能性の欠如により、堅牢性やプライバシー保護などの深刻な問題に直面しています。

これらのモデルの説明可能性の欠如は、予測や決定に対する信頼の欠如につながる可能性があり、そのため、モデルの実用的な応用が制限される可能性があります。重要な分野

量子情報と多体物理学に基づく Tensor ネットワークは、ML への「ホワイト ボックス」アプローチを提供します。研究者らは、「テンソル ネットワークは、量子の概念、理論、手法を ML と結び付け、テンソル ネットワーク ベースの ML を効果的に実装する上で重要な役割を果たします。」

From Quantum のための強力な「ホワイト ボックス」数学ツール物理 量子物理学は、強力な「ホワイト ボックス」数学ツールを生み出しました。

古典的コンピューティングと量子コンピューティングの急速な発展に伴い、TN は、解釈可能性と効率性の間のジレンマを克服するための新しいアイデアを提供します。 TN は、複数のテンソルの短縮として定義されます。そのネットワーク構造は、テンソルがどのように縮小するかを決定します。

図 1 に、3 つのタイプの TN を図で示します。これら 3 つのタイプは、行列積状態 (MPS) 表現、ツリー TN、投影エンタングルドペア状態 (PEPS) 表現です。

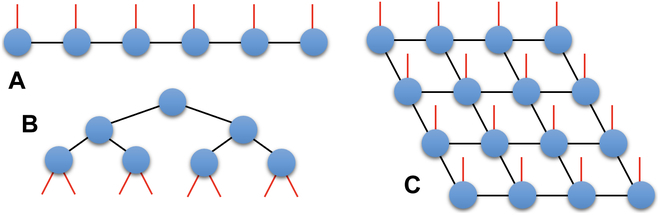
図 1: 3 つのタイプの TN の図式表現: ( A) MPS、(B) ツリー TN、および (C) PEPS。 (出典: 論文)

TN は、大規模な量子システムの状態を効率的に表現するものとして、量子力学の分野で目覚ましい成功を収めています。 TN 理論では、もつれエントロピー面積法則を満たす状態は、有限の結合次元をもつ TN 表現によって効率的に近似できます。

密度行列くり込み群や時間発展ブロック抽出などの MPS ベースのアルゴリズムは、もつれエントロピーのシミュレーションにおいて大幅な効率を示します。さらに、MPS は、グリーンバーガー・ホーン・ツァイリンガー状態や W 状態など、量子情報処理や計算で広く使用されている多くの人工的に構築された状態を表すこともできます。

PEPS は、2 次元以上の面積法則への準拠を表し、高次元量子システムの研究で大きな成功を収めています。要約すると、もつれエントロピーの面積法則は、量子システムのシミュレーションにおける TN の表現または計算能力の本質的な説明を提供します。この説明は TN ML にも当てはまります。さらに、ML の (古典的な) 確率モデルと同様に、「ホワイト ボックス」数値ツール (ボーン マシン) としての TN は、ボーンの量子確率解釈 (ボーンの法則とも呼ばれます) によって説明できます

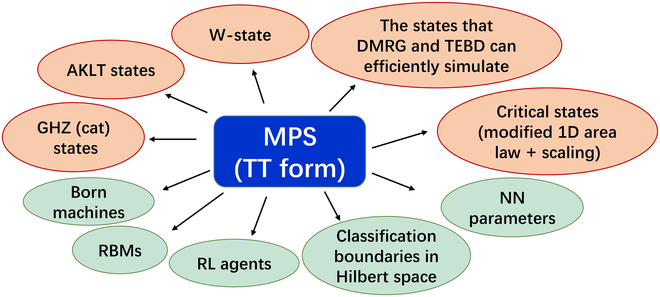
図 2: MPS (Tensor Train 形式) を使用すると、多数の数学的オブジェクトを効果的に表現または定式化できます。 (引用元: 論文)

量子に触発された機械学習の技術進歩

TN は、その確かな理論と効果的な手法により、機械学習における解釈可能性と効率性の間のジレンマを解決する新しい方法を提供します。現在、絡み合った 2 つの研究系統が議論されています:

1. 量子理論は、TN ML 解釈可能性の数学的基礎としてどのように機能しますか?
2. 量子力学の TN メソッドと量子コンピューティング技術は、どのようにして効率的な TN ML ソリューションを生み出すのでしょうか?

この記事では、研究者が、特徴マッピング、モデリング、量子コンピューティング ベースの ML の観点から、量子にインスピレーションを得た ML における最近の心強い進歩を紹介します。問題について説明しました。これらの進歩は、効率と解釈可能性の向上における TN の使用の利点と密接に関連しています。これらの ML アプローチは、その理論、モデル、手法が量子物理学に由来しているか、量子物理学からインスピレーションを得ているため、「量子にインスピレーションを得た」と呼ばれることがよくあります。ただし、量子物理学に基づいた解釈可能性のためのシステム フレームワークを開発するには、さらなる努力が必要です

次の表に、TN ML に関する主な手法と、それらの効率および解釈可能性との関係をまとめます。

#古典的な機械学習を強化する技術ネットワーク

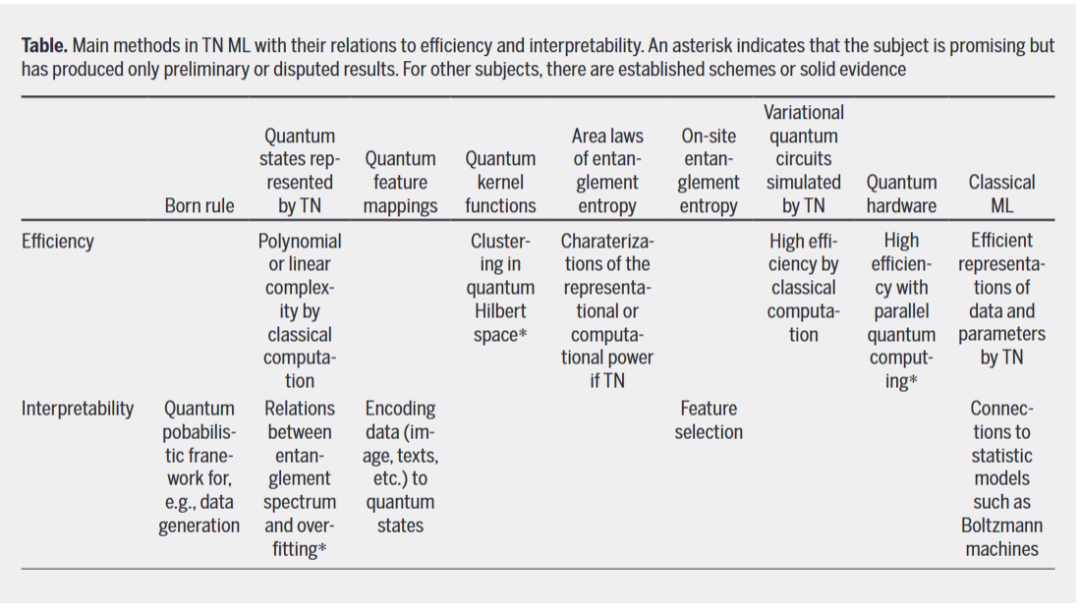
基本的な数学ツールとして、ML でのニューラル ネットワークの応用は次のような応用に限定されません。量子確率的解釈。 TN を使用すると、イジング モデルやポッツ モデルなどの古典的な確率システムの分配関数を効果的に表現およびシミュレートできるため、TN とボルツマン マシンの関係は広範囲に研究されてきました。

TN は、確率的解釈を無視して、NN を強化し、新しい ML モデルを開発するためにも使用されます。 中国語に書き直すと： TN は、確率的説明を無視して、NN を強化し、新しい ML モデルを開発するためにも使用されます。

同じ根拠に基づいて、NN の変分パラメータを TN に分解するか、変分パラメータを直接変更するモデル圧縮方法が提案されています。 TNとして。後者は明示的な分解プロセスを必要としない場合があり、ニューラル ネットワークのパラメーターはテンソルではなく、TT 形式、行列積演算子、またはディープ TN に直接復元されます。 ML パフォーマンスを向上させるために、TN に非線形活性化関数が追加され、TN を多重線形モデルから非線形モデルに一般化します。

書き直す必要があるのは次のとおりです: 結論

長い間、人々は人工知能 (特に深層機械学習）のジレンマ。これに関して、解釈可能で効率的な量子にヒントを得た機械学習手法である TN による心強い進歩をレビューします。

図 3 の「N ML バタフライ」には、ML における TN の利点がリストされています。量子にインスピレーションを得た ML の場合、TN の利点は 2 つの重要な側面に要約できます。1 つは解釈可能性のための量子理論、もう 1 つは効率向上のための量子手法です。一方では、TN を使用すると、統計と量子理論 (エンタングルメント理論など) を適用して、古典的な情報や統計理論で説明できるものを超える可能性のある解釈可能性のための確率論的な枠組みを構築できます。一方、強力な量子力学 TN アルゴリズムと大幅に強化された量子コンピューティング テクノロジーにより、量子にインスピレーションを得た TN ML 手法が古典的コンピューティング プラットフォームと量子コンピューティング プラットフォームの両方で非常に効率的になることが可能になります。

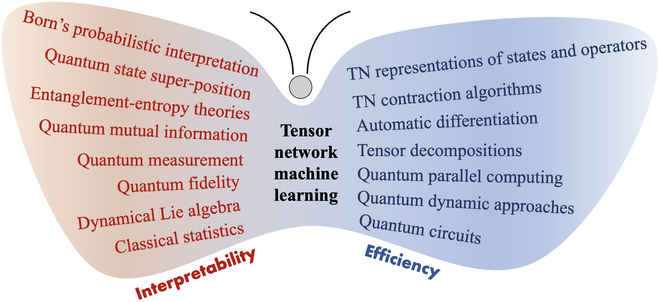図 3: 「TN ML バタフライ」は、量子理論に基づく解釈可能性 (左翼) と量子手法に基づく効率 (右翼) という 2 つの独自の利点を要約しています。 (出典: 論文)

特に、GPT 分野における最近の大幅な進歩により、モデルの複雑さと計算能力が前例のないほど急増しており、TN ML に新たな機会と課題をもたらしています。 GPT AI の出現に直面して、説明可能性は研究効率を向上させるだけでなく、現在の NISQ 時代と今後の量子コンピューティングの真の時代において、より優れたアプリケーションとより安全な制御を可能にするために、ますます価値が高まっています。理論、モデル、アルゴリズム、ソフトウェア、ハードウェア、アプリケーションなどのさまざまな観点から量子人工知能を探索するための重要な数学的ツールとして急速に成長しています。 news/2023-11-tensor-networks-efficiency-quantum-inspired-machine.html

以上が国立科学技術大学と第一師範大学の協力の概要: 「ホワイト ボックス」テンソル ネットワークが量子機械学習の解釈可能性と効率をどのように改善できるかを明らかにするの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。