機械学習モデルのパフォーマンスを示す 10 の指標
大規模モデルは非常に強力ですが、実際の問題の解決は必ずしも大規模モデルに完全に依存するわけではありません。必ずしも量子力学を使用せずに現実の物理現象を説明するための、あまり正確ではないアナロジー。いくつかの比較的単純な問題の場合は、おそらく統計的分布で十分でしょう。機械学習にはディープラーニングやニューラルネットワークが必要なのは言うまでもありませんが、重要なのは問題の境界を明確にすることです。
では、ML を使用して比較的単純な問題を解決する場合、機械学習モデルのパフォーマンスをどのように評価すればよいでしょうか?産業界や研究生の参考になればと思い、比較的よく使われる10の評価指標を紹介します。
1. 精度
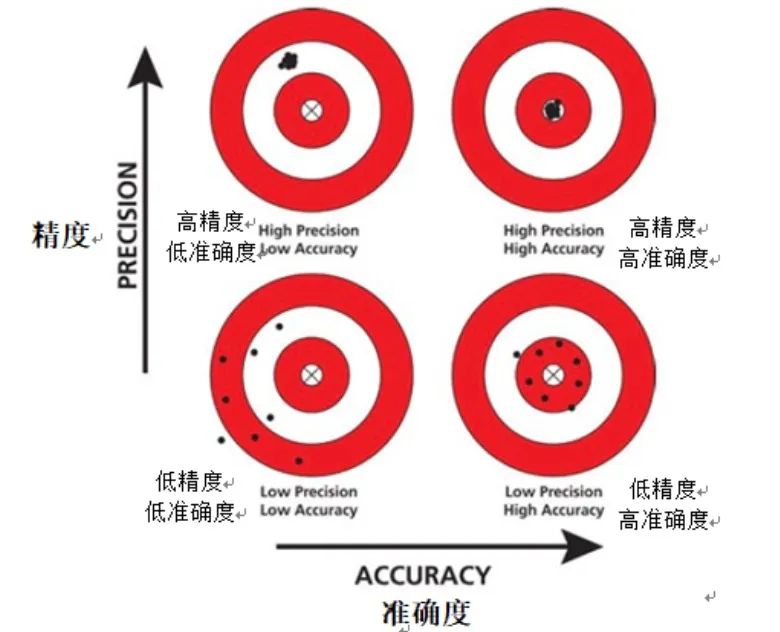
精度は機械学習の分野における基本的な評価指標であり、通常、モデルのパフォーマンスを迅速に理解するために使用されます。精度は、データセット内のインスタンスの総数に対するモデルによって正しく予測されたインスタンス数の比率を単純に計算することで、モデルの精度を測定する直感的な方法を提供します。
 写真
写真
ただし、不均衡なデータセットを扱う場合、評価指標としての精度が不十分になる可能性があります。不均衡なデータ セットとは、特定のカテゴリのインスタンス数が他のカテゴリのインスタンス数を大幅に上回っているデータ セットを指します。この場合、モデルはより多くのカテゴリを予測する傾向があり、その結果、誤って高い精度が得られる可能性があります。
さらに、精度からは偽陽性と偽陰性に関する情報は得られません。偽陽性は、モデルが陰性インスタンスを陽性インスタンスとして誤って予測する場合であり、偽陰性は、モデルが陽性インスタンスを陰性インスタンスとして誤って予測する場合です。モデルのパフォーマンスを評価する場合、偽陽性と偽陰性はモデルのパフォーマンスに異なる影響を与えるため、これらを区別することが重要です。
要約すると、精度はシンプルでわかりやすい評価指標ですが、不均衡なデータセットを扱う場合は、精度の結果を解釈する際により注意する必要があります。
2. 精度
精度は重要な評価指標であり、陽性サンプルに対するモデルの予測精度の測定に焦点を当てています。精度とは異なり、精度は、モデルによって正であると予測されたインスタンスのうち、実際に正であるインスタンスの割合を計算します。言い換えれば、精度は、「モデルがインスタンスを正であると予測するとき、この予測が正確である確率はどのくらいですか?」という質問に答えます。高精度モデルとは、インスタンスが正であると予測するときに、このインスタンスが実際に陽性サンプルである可能性が非常に高いです。
 写真
写真
医療診断や不正行為検出などの一部のアプリケーションでは、モデルの精度が特に重要です。これらのシナリオでは、偽陽性 (つまり、陰性サンプルを陽性サンプルとして誤って予測すること) の結果が非常に深刻になる可能性があります。例えば、医療診断においては、偽陽性の診断により不必要な治療や検査が行われ、患者に不必要な精神的・身体的ストレスを与える可能性がある。不正検出では、誤検知により、無実のユーザーが不正行為者として誤ってラベル付けされ、ユーザー エクスペリエンスと会社の評判に影響を与える可能性があります。
したがって、これらのアプリケーションでは、モデルの精度が高いことを確認することが重要です。精度を向上させることによってのみ、誤検知のリスクを軽減し、誤検知による悪影響を軽減することができます。
3. 再現率
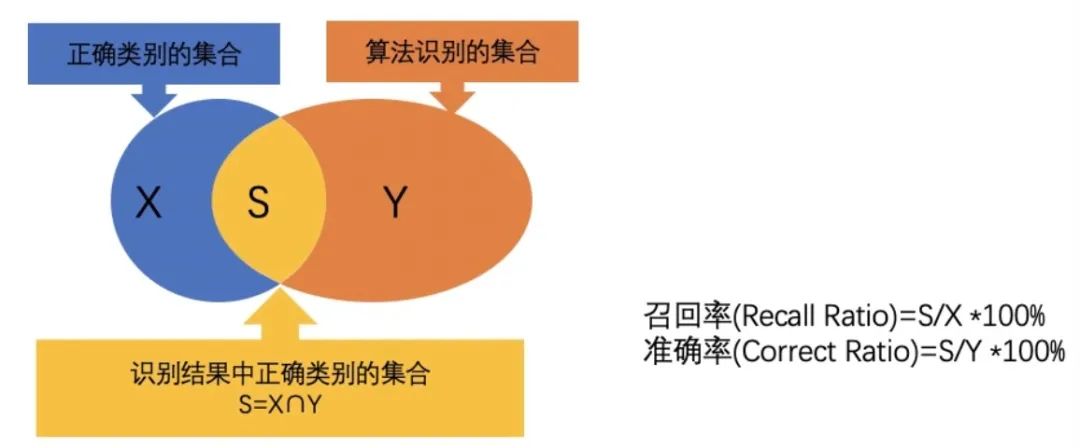
再現率は重要な評価指標であり、すべての実際の陽性サンプルを正確に予測するモデルの能力を測定するために使用されます。具体的には、再現率は、モデルによって真陽性であると予測されたインスタンスの実際の陽性例の総数に対する比率として計算されます。このメトリクスは、「モデルは実際の肯定的な例のうちいくつを正確に予測しましたか?」という質問に答えます。
精度とは異なり、再現率は、実際の肯定的な例を想起するモデルの能力に焦点を当てます。モデルの特定の陽性サンプルに対する予測確率が低い場合でも、そのサンプルが実際に陽性サンプルであり、モデルによって陽性サンプルとして正しく予測されている限り、この予測は再現率の計算に含まれます。 。したがって、再現率では、予測確率が高いサンプルだけでなく、モデルができるだけ多くの陽性サンプルを見つけられるかどうかがより重要になります。
 図
図
一部のアプリケーション シナリオでは、再現率の重要性が特に顕著になります。たとえば、病気の検出において、モデルが実際の病気の患者を見逃した場合、病気の遅延や悪化を引き起こし、患者に重大な結果をもたらす可能性があります。別の例として、顧客の離脱予測において、モデルが離脱する可能性の高い顧客を正確に特定できない場合、企業は維持策を講じる機会を失い、その結果、重要な顧客を失う可能性があります。
したがって、これらのシナリオでは、再現率が重要な指標になります。再現率が高いモデルは、実際の陽性サンプルをより適切に検出できるため、漏れのリスクが軽減され、起こり得る深刻な結果を回避できます。
4. F1 スコア
F1 スコアは、適合率と再現率のバランスをとることを目的とした総合的な評価指標です。これは実際には適合率と再現率の調和平均であり、これら 2 つの指標を 1 つのスコアに組み合わせて、偽陽性と偽陰性の両方を考慮した評価方法を提供します。
 図
図
多くの実際のアプリケーションでは、多くの場合、精度と再現率の間でトレードオフを行う必要があります。精度はモデルの予測の正しさに焦点を当て、再現率はモデルが実際のすべての陽性サンプルを見つけることができるかどうかに焦点を当てます。ただし、一方の指標を強調しすぎると、もう一方の指標のパフォーマンスが損なわれる場合があります。たとえば、再現率を向上させるために、モデルは陽性サンプルの予測を増やすことができますが、これにより偽陽性の数も増えるため、精度が低下する可能性があります。
F1 スコアリングは、この問題を解決するために設計されました。精度と再現率が考慮され、別のメトリクスを最適化するためにあるメトリクスを犠牲にすることがなくなります。精度と再現率の調和平均を計算することにより、F1 スコアは 2 つのバランスをとり、どちらの側にも有利になることなくモデルのパフォーマンスを評価できるようになります。
したがって、F1 スコアは、精度と再現率を考慮したメトリクスが必要で、一方のメトリクスを他方よりも優先したくない場合に非常に便利なツールです。これは、モデルのパフォーマンスを評価するプロセスを簡素化する単一のスコアを提供し、現実世界のアプリケーションでモデルがどのように実行されるかをより深く理解するのに役立ちます。
5. ROC-AUC
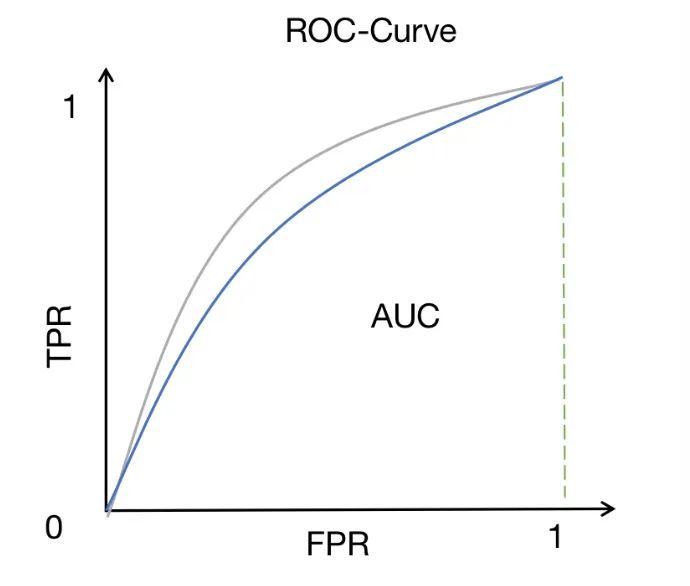
ROC-AUC は、バイナリ分類問題で広く使用されているパフォーマンス測定方法です。これは、ROC 曲線の下の面積を測定します。ROC 曲線は、さまざまなしきい値での真陽性率 (感度またはリコールとも呼ばれます) と偽陽性率の関係を示します。
 図
図
ROC 曲線は、さまざまなしきい値設定の下でモデルのパフォーマンスを観察する直感的な方法を提供します。しきい値を変更することで、モデルの真陽性率と偽陽性率を調整して、異なる分類結果を取得できます。 ROC 曲線が左上隅に近づくほど、陽性サンプルと陰性サンプルを区別する際のモデルのパフォーマンスが向上します。
AUC (曲線下面積) は、モデルの識別能力を評価するための定量的な指標を提供します。 AUC 値は 0 から 1 の間です。1 に近いほど、モデルの識別能力が強くなります。 AUC スコアが高いということは、モデルが陽性サンプルと陰性サンプルを適切に区別できること、つまり、モデルによる陽性サンプルの予測確率が陰性サンプルの予測確率よりも高いことを意味します。
したがって、ROC-AUC は、クラスを区別するモデルの能力を評価する場合に非常に便利なメトリクスです。他の指標と比較して、ROC-AUC にはいくつかの独自の利点があります。しきい値の選択に影響されず、さまざまなしきい値の下でのモデルのパフォーマンスを包括的に考慮できます。さらに、ROC-AUC はクラスの不均衡問題に対して比較的堅牢であり、正サンプルと負サンプルの数が不均衡な場合でも、意味のある評価結果を与えることができます。
ROC-AUC は非常に価値のあるパフォーマンス指標であり、特にバイナリ分類問題に適しています。さまざまなモデルの ROC-AUC スコアを観察して比較することで、モデルのパフォーマンスをより包括的に理解し、より優れた識別能力を持つモデルを選択できます。
6. PR-AUC
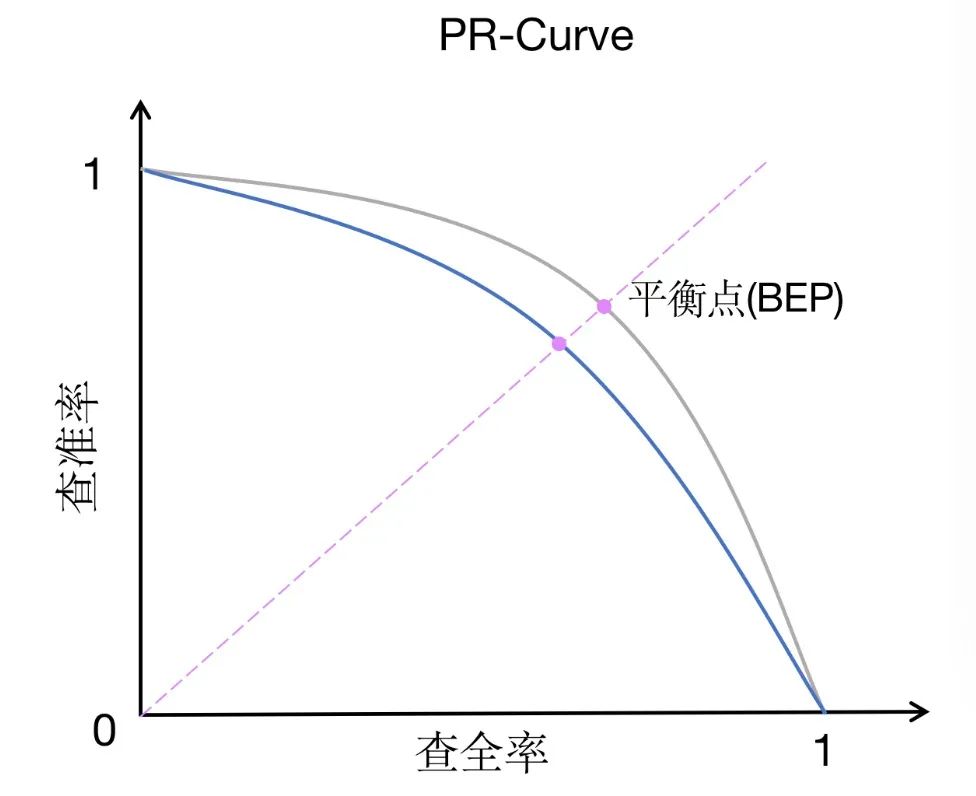
PR-AUC (適合率-再現率曲線下の面積) は ROC-AUC に似たパフォーマンス測定方法ですが、焦点が少し異なります。 PR-AUC は、適合率と再現率の曲線の下の面積を測定します。これは、さまざまなしきい値での適合率と再現率の関係を示します。
 写真
写真
ROC-AUC と比較して、PR-AUC は精度と再現率の間のトレードオフにさらに注意を払っています。適合率は、モデルが陽性であると予測したインスタンスのうち、実際に陽性であるインスタンスの割合を測定します。一方、再現率は、実際に陽性であるすべてのインスタンスのうち、モデルが陽性であると正しく予測したインスタンスの割合を測定します。精度と再現率のトレードオフは、不均衡なデータセットの場合、または偽陰性よりも偽陽性の方が懸念される場合に特に重要です。
不均衡なデータセットでは、あるカテゴリのサンプル数が別のカテゴリのサンプル数をはるかに超える可能性があります。この場合、ROC-AUC はクラスの不均衡を直接考慮せず、主に真陽性率と偽陽性率の関係に焦点を当てているため、ROC-AUC はモデルのパフォーマンスを正確に反映していない可能性があります。対照的に、PR-AUC は、精度と再現率の間のトレードオフを通じてモデルのパフォーマンスをより包括的に評価し、不均衡なデータセットに対するモデルの効果をより適切に反映できます。
さらに、PR-AUC は、偽陰性よりも偽陽性が懸念される場合にも、より適切な指標となります。一部のアプリケーション シナリオでは、陰性サンプルを陽性サンプルとして誤って予測する (偽陽性) と、より大きな損失や悪影響が生じる可能性があるためです。たとえば、医療診断において、健康な人を病気の人として誤って診断すると、不必要な治療や不安を引き起こす可能性があります。この場合、誤検知の数を減らすために、モデルの精度が高いことが望ましいと考えられます。
要約すると、PR-AUC は、不均衡なデータセットや誤検知が懸念されるシナリオに適したパフォーマンス測定方法です。これは、モデルの精度と再現率の間のトレードオフをより深く理解し、実際のニーズを満たす適切なモデルを選択するのに役立ちます。
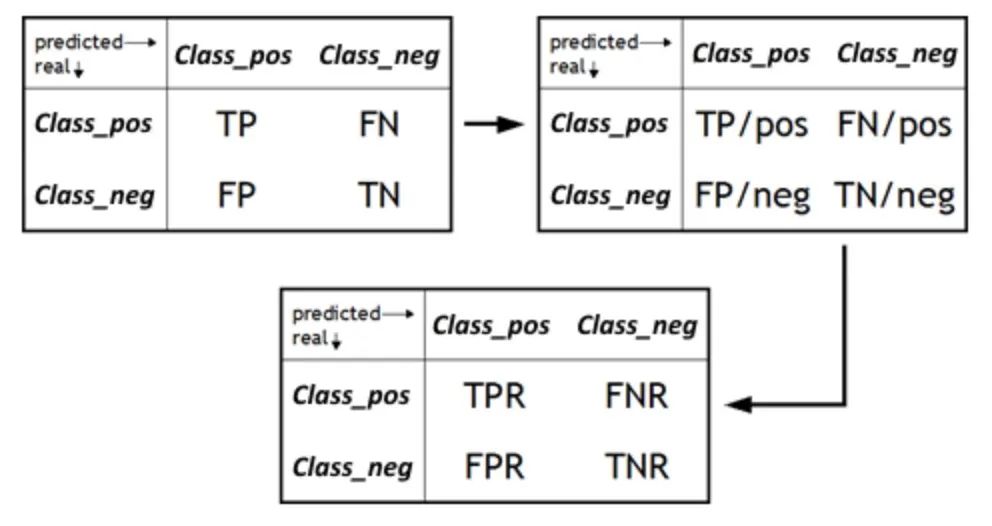
7. FPR/TNR
偽陽性率 (FPR) は、実際のすべての陰性サンプルのうち、モデルが誤って陽性と予測したサンプルの割合を測定する重要な指標です。これは特異性の補足的な指標であり、真陰性率 (TNR) に対応します。 FPR は、モデルの誤検知を回避する能力を評価する場合に重要な要素になります。誤検知は不必要な心配やリソースの無駄につながる可能性があるため、実際のアプリケーションにおけるモデルの信頼性を判断するには、モデルの FPR を理解することが重要です。 FPR を減らすことで、モデルの精度と精度を向上させ、陽性サンプルが実際に存在する場合にのみ陽性予測が発行されるようにすることができます。
 図
図
一方、特異性とも呼ばれる真陰性率 (TNR) は、モデルがどの程度正確に識別しているかを示す尺度です。ネガティブサンプルのインデックス。実際の合計陰性に対する、モデルによって真陰性であると予測されたインスタンスの割合を計算します。モデルを評価するとき、多くの場合、モデルが陽性サンプルを識別する能力に焦点を当てますが、同様に重要なのは、陰性サンプルを識別するモデルのパフォーマンスです。高い TNR は、モデルが陰性サンプルを正確に識別できることを意味します。つまり、実際に陰性サンプルであるインスタンスの中で、モデルはより高い割合の陰性サンプルを予測します。これは、誤検知を回避し、モデルの全体的なパフォーマンスを向上させるために非常に重要です。
8. マシューズ相関係数 (MCC)
MCC (マシューズ相関係数) は、二値分類問題で使用される尺度であり、真陽性と真陰性の関係について包括的な考慮を提供します。 、偽陽性と偽陰性が評価されます。他の測定方法と比較した場合、MCC の利点は、-1 から 1 の範囲の単一の値であることです。-1 はモデルの予測が実際の結果と完全に一致しないことを意味し、1 はモデルの予測が完全に一致することを意味します実際の結果です。
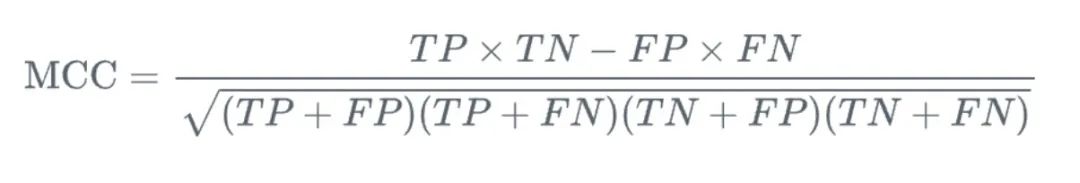 写真
写真
さらに重要なのは、MCC はバイナリ分類の品質を測定するバランスの取れた方法を提供することです。バイナリ分類問題では、通常、陽性サンプルと陰性サンプルを識別するモデルの能力に焦点を当てますが、MCC は両方の側面を考慮します。これは、モデルが陽性サンプル (つまり、真陽性) を正確に予測する能力だけでなく、モデルが陰性サンプル (つまり、真陰性) を正確に予測する能力にも焦点を当てています。同時に、MCC はモデルのパフォーマンスをより包括的に評価するために、偽陽性と偽陰性も考慮します。
実際のアプリケーションでは、MCC は不均衡なデータ セットを処理するのに特に適しています。不均衡なデータセットでは、あるカテゴリのサンプル数が別のカテゴリのサンプル数よりもはるかに大きいため、多くの場合、より大きな数を持つカテゴリを予測する方向にモデルが偏ります。ただし、MCC は 4 つの指標 (真陽性、真陰性、偽陽性、偽陰性) をすべてバランスよく考慮できるため、一般に不均衡なデータ セットに対してより正確かつ包括的なパフォーマンス評価を提供できます。
一般に、MCC は強力かつ包括的なバイナリ分類パフォーマンス測定ツールです。考えられるすべての予測結果を考慮するだけでなく、予測と実際の結果の一貫性を測定するための直感的で明確に定義された数値も提供します。バランスのとれたデータセットであっても、アンバランスなデータセットであっても、MCC はモデルのパフォーマンスをより深く理解するのに役立つ便利なメトリクスです。
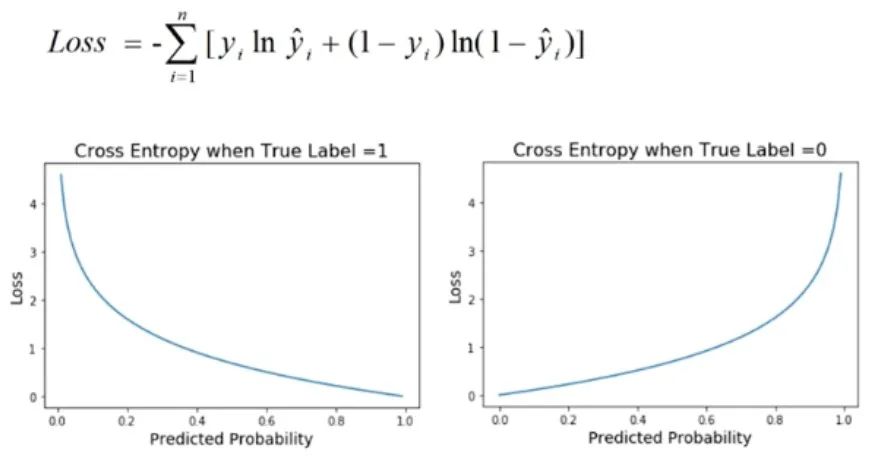
9. クロス エントロピー ロス
クロス エントロピー ロスは、特にモデルの出力が確率値である場合に、分類問題で一般的に使用されるパフォーマンス メトリックです。この損失関数は、モデルによって予測された確率分布と実際のラベル分布の間の差異を定量化するために使用されます。
 図
図
分類問題では、通常、モデルの目標は、サンプルが異なるカテゴリに属する確率を予測することです。クロスエントロピー損失は、モデルの予測確率と実際のバイナリ結果の間の一貫性を評価するために使用されます。予測された確率の対数を取得し、それを実際のラベルと比較することで損失値を導き出します。したがって、クロスエントロピー損失は対数損失とも呼ばれます。
クロスエントロピー損失の利点は、確率分布のモデルの予測精度を適切に測定できることです。モデルの予測確率分布が実際のラベル分布と類似している場合、クロスエントロピー損失の値は低くなり、逆に、予測確率分布が実際のラベル分布と大きく異なる場合、クロスエントロピー損失の値は高い。したがって、クロスエントロピー損失値が低いということは、モデルの予測がより正確であること、つまりモデルのキャリブレーション パフォーマンスが高いことを意味します。
実際のアプリケーションでは、通常、より低いクロスエントロピー損失値を追求します。これは、分類問題に対するモデルの予測がより正確で信頼できることを意味するためです。クロスエントロピー損失を最適化することで、モデルのパフォーマンスを向上させ、実際のアプリケーションでの汎化能力を向上させることができます。したがって、クロスエントロピー損失は、分類モデルのパフォーマンスを評価するための重要な指標の 1 つであり、モデルの予測精度や、モデルのパラメーターと構造のさらなる最適化が必要かどうかをさらに理解するのに役立ちます。
10. コーエンのカッパ係数
コーエンのカッパ係数は、モデルの予測と実際のラベルの間の一貫性を測定するために使用される統計ツールであり、分類タスクの評価に特に適しています。他の測定方法と比較して、モデルの予測と実際のラベルの単純な一致を計算するだけでなく、偶然に発生する可能性のある一致を補正するため、より正確で信頼性の高い評価結果が得られます。
実際のアプリケーションでは、特に複数の評価者が同じサンプル セットの分類に関与する場合、コーエンのカッパ係数は非常に役立ちます。この場合、モデル予測と実際のラベルの一貫性に焦点を当てる必要があるだけでなく、異なる評価者間の一貫性も考慮する必要があります。評価者間に大きなばらつきがあると、モデルの性能の評価結果が評価者の主観に左右され、不正確な評価結果が得られる可能性があるためです。
コーエンのカッパ係数を使用すると、偶然に発生する可能性のあるこの一貫性を補正でき、モデルのパフォーマンスをより正確に評価できるようになります。具体的には、-1 から 1 までの値を計算します。1 は完全な一貫性を表し、-1 は完全な不一貫性を表し、0 はランダムな一貫性を表します。したがって、カッパ値が高いということは、モデルの予測と実際のラベルの間の一致が、偶然に予想される一致を超えていることを意味し、モデルのパフォーマンスが優れていることを示します。
 図
図
コーエンのカッパ係数は、分類タスクの一貫性におけるモデルの予測と実際のラベルの間のギャップをより正確に評価するのに役立ちます。偶然に発生する可能性のある一貫性を修正しながら。より客観的で正確な評価を提供できるため、複数の評価者が関与するシナリオでは特に重要です。
概要
機械学習モデルの評価には多くの指標があります。この記事では主な指標のいくつかを示します:
- 精度: 正確に予測された数値の比率サンプルの総数に対するサンプルの数。
- 精度: 予測されたすべての陽性 (TP および FP) サンプルに対する真陽性 (TP) サンプルの割合。これは、陽性サンプルを識別するモデルの能力を反映しています。
- 思い出してください: すべての真陽性 (TP および FN) サンプルに対する真陽性 (TP) サンプルの割合。これは、陽性サンプルを検出するモデルの能力を反映しています。
- F1 値: 精度と再現率の両方を考慮した、精度と再現率の調和平均。
- ROC-AUC: ROC 曲線の下の面積ROC 曲線は、真陽性率 (真陽性率、TPR) と偽陽性率 (偽陽性率、FPR) の関数です。 AUC が大きいほど、モデルの分類パフォーマンスが向上します。
- PR-AUC: 適合率と再現率の曲線の下の領域。適合率と再現率のトレードオフに焦点を当てており、不均衡なデータセットにより適しています。
- FPR/TNR: FPR は偽陽性を報告するモデルの能力を測定し、TNR は陰性サンプルを正しく識別するモデルの能力を測定します。
- クロスエントロピー損失: モデルの予測確率と実際のラベルの差を評価するために使用されます。値が低いほど、モデルのキャリブレーションと精度が優れていることを示します。
- Matthews Correlation Coefficient (MCC): 真陽性、真陰性、偽陽性、および偽陰性の間の関係を考慮に入れるメトリクスで、バイナリ分類の品質のバランスの取れた尺度を提供します。
- Cohen's kappa: 分類タスクにおけるモデルのパフォーマンスを評価するための重要なツールです。特に複数の評価者のシナリオにおいて、予測とラベルの間の一貫性を正確に測定し、偶発的な一貫性を修正できます。利点。
上記の各インジケーターには独自の特性があり、さまざまな問題シナリオに適しています。実際のアプリケーションでは、モデルのパフォーマンスを包括的に評価するために複数の指標を組み合わせる必要がある場合があります。
以上が機械学習モデルのパフォーマンスを示す 10 の指標の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7487
7487
 15
15
 1377
1377
 52
52
 77
77
 11
11
 19
19
 39
39
 C++ での機械学習アルゴリズムの実装: 一般的な課題と解決策
Jun 03, 2024 pm 01:25 PM
C++ での機械学習アルゴリズムの実装: 一般的な課題と解決策
Jun 03, 2024 pm 01:25 PM
C++ の機械学習アルゴリズムが直面する一般的な課題には、メモリ管理、マルチスレッド、パフォーマンスの最適化、保守性などがあります。解決策には、スマート ポインター、最新のスレッド ライブラリ、SIMD 命令、サードパーティ ライブラリの使用、コーディング スタイル ガイドラインの遵守、自動化ツールの使用が含まれます。実践的な事例では、Eigen ライブラリを使用して線形回帰アルゴリズムを実装し、メモリを効果的に管理し、高性能の行列演算を使用する方法を示します。
 OpenAI データは必要ありません。大規模なコード モデルのリストに加わりましょう。 UIUC が StarCoder-15B-Instruct をリリース
Jun 13, 2024 pm 01:59 PM
OpenAI データは必要ありません。大規模なコード モデルのリストに加わりましょう。 UIUC が StarCoder-15B-Instruct をリリース
Jun 13, 2024 pm 01:59 PM
ソフトウェア テクノロジの最前線に立つ UIUC Zhang Lingming のグループは、BigCode 組織の研究者とともに、最近 StarCoder2-15B-Instruct 大規模コード モデルを発表しました。この革新的な成果により、コード生成タスクにおいて大きな進歩が達成され、CodeLlama-70B-Instruct を上回り、コード生成パフォーマンス リストのトップに到達しました。 StarCoder2-15B-Instruct のユニークな特徴は、その純粋な自己調整戦略であり、トレーニング プロセス全体がオープンで透過的で、完全に自律的で制御可能です。このモデルは、高価な手動アノテーションに頼ることなく、StarCoder-15B 基本モデルの微調整に応じて、StarCoder2-15B を介して数千の命令を生成します。
 説明可能な AI: 複雑な AI/ML モデルの説明
Jun 03, 2024 pm 10:08 PM
説明可能な AI: 複雑な AI/ML モデルの説明
Jun 03, 2024 pm 10:08 PM
翻訳者 | Li Rui によるレビュー | 今日、人工知能 (AI) および機械学習 (ML) モデルはますます複雑になっており、これらのモデルによって生成される出力はブラックボックスになっており、関係者に説明することができません。 Explainable AI (XAI) は、利害関係者がこれらのモデルがどのように機能するかを理解できるようにし、これらのモデルが実際に意思決定を行う方法を確実に理解できるようにし、AI システムの透明性、信頼性、およびこの問題を解決するための説明責任を確保することで、この問題を解決することを目指しています。この記事では、さまざまな説明可能な人工知能 (XAI) 手法を検討して、その基礎となる原理を説明します。説明可能な AI が重要であるいくつかの理由 信頼と透明性: AI システムが広く受け入れられ、信頼されるためには、ユーザーは意思決定がどのように行われるかを理解する必要があります
 Yolov10: 詳細な説明、展開、アプリケーションがすべて 1 か所にまとめられています。
Jun 07, 2024 pm 12:05 PM
Yolov10: 詳細な説明、展開、アプリケーションがすべて 1 か所にまとめられています。
Jun 07, 2024 pm 12:05 PM
1. はじめに ここ数年、YOLO は、計算コストと検出パフォーマンスの効果的なバランスにより、リアルタイム物体検出の分野で主流のパラダイムとなっています。研究者たちは、YOLO のアーキテクチャ設計、最適化目標、データ拡張戦略などを調査し、大きな進歩を遂げました。同時に、後処理に非最大抑制 (NMS) に依存すると、YOLO のエンドツーエンドの展開が妨げられ、推論レイテンシに悪影響を及ぼします。 YOLO では、さまざまなコンポーネントの設計に包括的かつ徹底的な検査が欠けており、その結果、大幅な計算冗長性が生じ、モデルの機能が制限されます。効率は最適ではありませんが、パフォーマンス向上の可能性は比較的大きくなります。この作業の目標は、後処理とモデル アーキテクチャの両方から YOLO のパフォーマンス効率の境界をさらに改善することです。この目的を達成するために
 あなたが知らない機械学習の 5 つの流派
Jun 05, 2024 pm 08:51 PM
あなたが知らない機械学習の 5 つの流派
Jun 05, 2024 pm 08:51 PM
機械学習は人工知能の重要な分野であり、明示的にプログラムしなくてもコンピューターにデータから学習して能力を向上させる機能を提供します。機械学習は、画像認識や自然言語処理から、レコメンデーションシステムや不正行為検出に至るまで、さまざまな分野で幅広く応用されており、私たちの生活様式を変えつつあります。機械学習の分野にはさまざまな手法や理論があり、その中で最も影響力のある 5 つの手法は「機械学習の 5 つの流派」と呼ばれています。 5 つの主要な学派は、象徴学派、コネクショニスト学派、進化学派、ベイジアン学派、およびアナロジー学派です。 1. 象徴主義は、象徴主義とも呼ばれ、論理的推論と知識の表現のためのシンボルの使用を強調します。この学派は、学習は既存の既存の要素を介した逆演繹のプロセスであると信じています。
 さまざまな Java フレームワークのパフォーマンスの比較
Jun 05, 2024 pm 07:14 PM
さまざまな Java フレームワークのパフォーマンスの比較
Jun 05, 2024 pm 07:14 PM
さまざまな Java フレームワークのパフォーマンス比較: REST API リクエスト処理: Vert.x が最高で、リクエスト レートは SpringBoot の 2 倍、Dropwizard の 3 倍です。データベース クエリ: SpringBoot の HibernateORM は Vert.x や Dropwizard の ORM よりも優れています。キャッシュ操作: Vert.x の Hazelcast クライアントは、SpringBoot や Dropwizard のキャッシュ メカニズムよりも優れています。適切なフレームワーク: アプリケーションの要件に応じて選択します。Vert.x は高パフォーマンスの Web サービスに適しており、SpringBoot はデータ集約型のアプリケーションに適しており、Dropwizard はマイクロサービス アーキテクチャに適しています。
 C++ の機械学習: C++ で一般的な機械学習アルゴリズムを実装するためのガイド
Jun 03, 2024 pm 07:33 PM
C++ の機械学習: C++ で一般的な機械学習アルゴリズムを実装するためのガイド
Jun 03, 2024 pm 07:33 PM
C++ では、機械学習アルゴリズムの実装には以下が含まれます。 線形回帰: 連続変数を予測するために使用されるステップには、データの読み込み、重みとバイアスの計算、パラメーターと予測の更新が含まれます。ロジスティック回帰: 離散変数の予測に使用されます。このプロセスは線形回帰に似ていますが、予測にシグモイド関数を使用します。サポート ベクター マシン: サポート ベクターの計算とラベルの予測を含む強力な分類および回帰アルゴリズム。
 清華大学が引き継ぎ、YOLOv10 が登場しました。パフォーマンスが大幅に向上し、GitHub のホット リストに掲載されました。
Jun 06, 2024 pm 12:20 PM
清華大学が引き継ぎ、YOLOv10 が登場しました。パフォーマンスが大幅に向上し、GitHub のホット リストに掲載されました。
Jun 06, 2024 pm 12:20 PM
ターゲット検出システムのベンチマークである YOLO シリーズが再び大幅にアップグレードされました。今年 2 月の YOLOv9 のリリース以来、YOLO (YouOnlyLookOnce) シリーズのバトンは清華大学の研究者の手に渡されました。先週末、YOLOv10 のリリースのニュースが AI コミュニティの注目を集めました。これは、コンピュータ ビジョンの分野における画期的なフレームワークと考えられており、リアルタイムのエンドツーエンドの物体検出機能で知られており、効率と精度を組み合わせた強力なソリューションを提供することで YOLO シリーズの伝統を継承しています。論文アドレス: https://arxiv.org/pdf/2405.14458 プロジェクトアドレス: https://github.com/THU-MIG/yo




