html5 Canvas 描画チュートリアル (6)—canvas_html5 で曲線を描画するための arcTo メソッドチュートリアルスキル-H5 チュートリアル-php.cn

html5 Canvas 描画チュートリアル (6)—canvas_html5 で曲線を描画するための arcTo メソッドチュートリアルスキル

WBOY

リリース： 2016-05-16 15:50:13

オリジナル

1537 人が閲覧しました

前回の記事では canvas の arc メソッドについて説明しましたが、この記事ではそれに関連する arcTo メソッドについて説明します。
arc と arcTo は名前からして似ています。 arcToも曲線を描く手法であり、彼が描く曲線も真円の円弧です。しかし、彼のパラメータは単に arc~
ctx.arcTo(x1,y1,x2,y2,radius); と互換性がありません。arcTo のパラメータには 2 つの点が含まれており、これらの 2 つの点は円の中心を表しません。最後のパラメータのみが円の半径であり、arcTo が円と何らかの関係があることを示します。
インターネット上には arcTo に関する記事がほとんどなく、ようやく外国の記事を見つけました。また、キャンバスを描画するための直感的なツールがないため、長い間推測に頼るしかありませんでした。。。
直感的に説明するために、補助的な方法を採用しました。arcTo が描かれているところはどこでも、lineTo を使用して対応する点を描き、それらの関係を確認します。補助線を引くだけです。

コードをコピーします

コードは次のとおりです:

var x0=100,
y0 = 400、
x1 = 500、
y1 = 400、
x2 = 450、
y2 = 450;
ctx.beginPath(); x0,y0 );
ctx.ストロークスタイル = "#f00";
ctx.arcTo(x1,y1,x2,y2,20); ();
ctx.beginPath();
ctx.ストロークスタイル = "rgba(0,0,0,0.5)";
ctx.moveTo(x0, y0);
ctx.lineTo(x1,y1);
ctx.fillText('x1,y1',x1 10,y1 10)
ctx.lineTo(x2,y2); .fillText( 'x2,y2',x2 10,y2)
ctx.blood();

コードはたくさんあるように見えますが、実際は非常に簡単です。座標値を保存するためにいくつかの変数を使用し、残りはキャンバス操作でした。
変数の説明: x0、y0 は開始点の座標、x1、y1 は最初の点の座標、x2、y2 は 2 番目の点の座標です。 lineTo で描いた直線は半透明の 1px の黒い線、arcTo で描いた線は 2px の赤い線です。
ページを更新すると、下の写真が表示されます。

この赤い線はフックのように見えると言わざるを得ません。
次に、arcTo のルールが見つかります。これは、実際には始点、最初の点、および 2 番目の点の 2 つの直線を通過し、夾角を形成します。これらの 2 つの直線はパラメータ円の接線でもあります。

円の半径によって、円が線に接する位置が決まります。ボールが死角に転がり込むのと同じように、ボールが小さいほど、ボールはより遠くまで転がり、死角に近づきます。大きいボールの場合はその逆になります。 canvas arcTo これは非常に深刻な学術問題です。YY にならないでください。

ボールを大きくしてみよう！

コードをコピーします

コードは次のとおりです: ctx.arcTo(x1, y1,x2 ,y2,50); //半径を 50 に変更します

写真のように、円弧が非常に大きくなり、直線に接していないことがわかります。
もちろん、接線は無限に伸びるので、実際には接線のままです。

探索を続け、円を大きくし続け、開始点と最初の点の間の距離を縮めます。 canvas arcTo

コードをコピーします

コードは次のとおりです。 var x0=400; / /開始点 x 座標が 100 から 400 に変化します ...

ctx.arcTo(x1,y1,x2,y2,100); //円の半径が 100 に増加すると表示されます。とても奇妙な形。

元々はフックだったのですが、突然曲がってしまい、しかも逆方向に曲がってしまいました！ワインボトルラックのような感じですね。

ただし、この円はまだ 2 つの線に接していることに注意してください。ただ、2 つの線の長さが円と一致しなくなっているだけです。彼は両方の回線をワイヤレスで延長しました。
このフックハンドルはいつ反転されますか?幾何学が得意な場合は、点と円の間の接線の方程式を理解することができます。

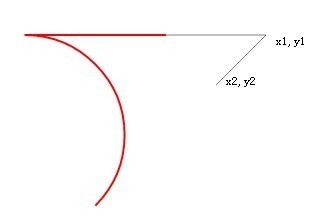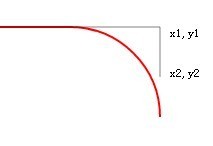
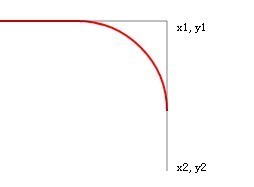arcTo メソッドには非常に重要な点があります。この重要な点は、コード内の (x1, y1) です。ただし、円の接点までの距離が開始点 (x0, y0) までの距離を超えています。）、逆転が起こります。 canvas arcTo 図から、点 (x2, y2) が常に接線上の点である限り、円の半径が変わらない限り、その座標は無限に変化することがわかります。 by arcTo 何も変わりません。これには特別な注意が必要です。