MATLAB を使用して sinc 関数の逆関数を解く方法を学習します。

MATLAB が sinc 関数の逆関数を解く方法を手伝ってください
k=1:length(y)の場合
f=@(x)y(k)*x-sin(x);
ezplot(f);%グラフを描いて、関数のゼロ点が x0(k) の近くにあることを観察します
z(k)=fzero(f,x0(k));% fzero 関数を呼び出してゼロ点を見つけます
endsxf2012 (サイトのtaに問い合わせてください)%% データとして y を例に取り、y の値が y0 であると仮定すると、
%f=@(x)y0-sin(x)/x;%%コマンドを使用: %ezplot(f);
%%絵を描いて関数を観察し、ゼロ点付近の座標 x0 を見つけます
%% したがって、必要なゼロ点は
になります。%z=fzero(f,x0);% fzero 関数を呼び出してゼロ点を見つけます
%たとえば、
を使用すると、y0=0.6f=@(x)0.6-sin(x)/x;%drawingezplot(f)hold onplot(,,'r')
%ゼロ点が -2 と 2 の近くにあることを確認し、
を使用します。z1=fzero(f,-2)
%計算されたゼロ点は x=-1.66
ですz2=fzero(f,2)
%計算されたゼロ点は x=1.66
ですこれは y=sinx/x のグラフです。私の場合、y の値はわかっているので、x のすべての値を取得する必要があります。つまり、逆関数を通じて取得したいと考えています。しかし、問題は、y=1 の場合、x は 1 つの値ですが、y=0.8 は 2 つの値、y=0.1 は多数の値であることです。
これは y=sinx/x のグラフです。私の場合、y の値はわかっているので、x のすべての値を取得する必要があります。つまり、逆関数を通じて取得したいと考えています。しかし...描画した区間では、関数は単調ではないため、その逆関数が存在しないか、多値関数です。
MATLAB で逆関数を作成する方法
finv
F 逆累積分布関数
###構文###XX = finv(P,V1,V2)
###説明###X = finv(P,V1,V2) は、P の対応する確率について、分子の自由度 V1 と分母の自由度 V2 を使用して F cdf の逆関数を計算します。P、V1、および V2 はベクトル、行列にすることができます。 、またはすべて同じサイズの多次元配列。スカラー入力は、他の入力と同じ次元の定数配列に拡張されます。
V1 と V2 のパラメーターはすべて正の整数である必要があり、P の値は [0 1] の範囲内にある必要があります。
F 逆関数は、F cdf に関して次のように定義されます。 ###どこ###
例分子の自由度 5、分母の自由度 10 の F 分布からサンプルの 95% を超える値を見つけます。
x = finv(0.95,5,10)
#xx =
3.3258
3.3258 を超える値が観測されるのは、確率の 5% だけです。
以上がMATLAB を使用して sinc 関数の逆関数を解く方法を学習します。の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7667
7667
 15
15
 1393
1393
 52
52
 1205
1205
 24
24
 91
91
 11
11
 Steam Cloudエラーを修正する方法は?これらの方法を試してください
Apr 04, 2025 am 01:51 AM
Steam Cloudエラーを修正する方法は?これらの方法を試してください
Apr 04, 2025 am 01:51 AM
Steam Cloudエラーは、多くの理由によって引き起こされる可能性があります。ゲームをスムーズにプレイするには、ゲームを開始する前にこのエラーを削除するためにいくつかの対策を講じる必要があります。 PHP.CNソフトウェアは、この投稿でより有用な情報と同様に、いくつかの最良の方法を紹介します。
 Windowsメタデータとインターネットサービスの問題:修正方法は?
Apr 02, 2025 pm 03:57 PM
Windowsメタデータとインターネットサービスの問題:修正方法は?
Apr 02, 2025 pm 03:57 PM
「Windowsメタデータとインターネットサービス(WMIS)への接続が確立できなかった」が表示される場合があります。イベントビューアのエラー。 PHP.CNからのこの投稿では、Windowsメタデータとインターネットサービスの問題を削除する方法を紹介します。
 KB5035942の更新問題を解決する方法 - クラッシュシステム
Apr 02, 2025 pm 04:16 PM
KB5035942の更新問題を解決する方法 - クラッシュシステム
Apr 02, 2025 pm 04:16 PM
KB5035942更新問題 - クラッシュシステムは一般にユーザーに発生します。 Imburitedの人々は、クラッシュするシステム、インストール、健全な問題など、一種のトラブルから抜け出す方法を見つけることを望んでいます。これらの状況をターゲットにして、この投稿はphp.cn wilが発行しました
 修正 - PCに写真をアップロードしないOneDrive
Apr 02, 2025 pm 04:04 PM
修正 - PCに写真をアップロードしないOneDrive
Apr 02, 2025 pm 04:04 PM
OneDriveは、Microsoftのオンラインクラウドストレージサービスです。時には、OneDriveがクラウドに写真をアップロードできないことがわかります。同じボートに乗っている場合は、PHP.CNソフトウェアからこの投稿を読んで、今すぐ効果的なソリューションを取得してください!
 Chris Titusツールを使用して、Debloated Win11/10 ISOを作成する方法
Apr 01, 2025 am 03:15 AM
Chris Titusツールを使用して、Debloated Win11/10 ISOを作成する方法
Apr 01, 2025 am 03:15 AM
Chris Titus Techには、Windowsユーティリティと呼ばれるツールがあります。これにより、Debloated Windows 11/10 ISOを簡単に作成してクリーンシステムをインストールできます。 PHP.CNは、Chris Titusツールを使用してこのことを行う方法に関する完全なガイドを提供しています。
 PC App Storeマルウェアを削除します - あなたのための完全なガイド!
Apr 04, 2025 am 01:41 AM
PC App Storeマルウェアを削除します - あなたのための完全なガイド!
Apr 04, 2025 am 01:41 AM
コンピューターにPC App Storeというプログラムがあり、意図的にインストールしていない場合は、PCがマルウェアに感染する可能性があります。 PHP.CNからのこの投稿では、PC App Storeマルウェアを削除する方法を紹介します。
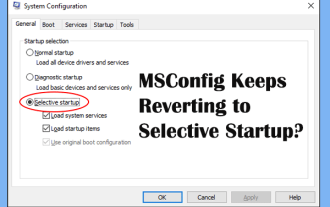 msconfigは選択的なスタートアップに戻り続けますか?ここで2つのソリューション
Mar 28, 2025 pm 12:06 PM
msconfigは選択的なスタートアップに戻り続けますか?ここで2つのソリューション
Mar 28, 2025 pm 12:06 PM
MsconfigがWindowsの選択的な起動に戻っているという問題について質問されていますか?必要な場合は、通常のスタートアップに切り替える方法は?このphp.cn投稿で説明されている方法を試して、あなたに合ったものを見つけてください。
 修正:兄弟:起動/読み込みではない2人の息子のリメイクの物語
Apr 02, 2025 am 02:40 AM
修正:兄弟:起動/読み込みではない2人の息子のリメイクの物語
Apr 02, 2025 am 02:40 AM
兄弟:2人の息子のリメイクの物語が起動していませんか?兄弟と出会う:2人の息子の物語が黒いスクリーンをリメイクしますか?ここでは、PHP.CNに関するこの投稿では、この問題に対処するのに役立つソリューションをテストしています。




