 テクノロジー周辺機器
テクノロジー周辺機器
 AI
AI
 ディープラーニングは幾何学的推論で天才レベルのパフォーマンスを達成 Nature が DeepMind のモデルを公開し、フィールズ賞受賞ニュースで賞賛を受ける
ディープラーニングは幾何学的推論で天才レベルのパフォーマンスを達成 Nature が DeepMind のモデルを公開し、フィールズ賞受賞ニュースで賞賛を受ける
ディープラーニングは幾何学的推論で天才レベルのパフォーマンスを達成 Nature が DeepMind のモデルを公開し、フィールズ賞受賞ニュースで賞賛を受ける
この成果は、AI の数学的推論能力における画期的な成果であり、一般的な AI システムの開発における重要なマイルストーンです。
今回、人工知能アルゴリズムは数学オリンピック (IMO) において大きな進歩を遂げました。
国際的に権威のある雑誌「Nature」の最新号に、AlphaGeometryと呼ばれる人工知能システムを紹介する論文が掲載されました。このシステムは、人による実演なしでオリンピックの幾何学問題を解決できます。専門家らは、これは人工知能が人間の推論能力を獲得するための進歩における重要なマイルストーンであると信じている。今回の研究成果の公表は、人工知能のさらなる発展を促進する上で非常に意義深いものです。

論文リンク: https://www.nature.com/articles/s41586-023-06747-5
DeepMind も論文に掲載されましたコードとモデルはしばらくオープンソース化されていました。GitHub: https://github.com/google-deepmind/alphageometry
これは、Google DeepMind## の手による人工知能システムです。 # の研究者は、人間のオリンピック金メダリストに近いレベルで複雑な幾何学的問題を解決できます。
数学オリンピックの幾何学問題 30 問のベンチマーク テストで、AlphaGeometry は数学オリンピックの標準制限時間内に幾何学問題のうち 25 問を解決しましたが、以前の最先端システムは幾何学問題のうち 10 問しか解決できませんでした。 。これに対し、人間の金メダリストは平均 25.9 問の問題を解きました。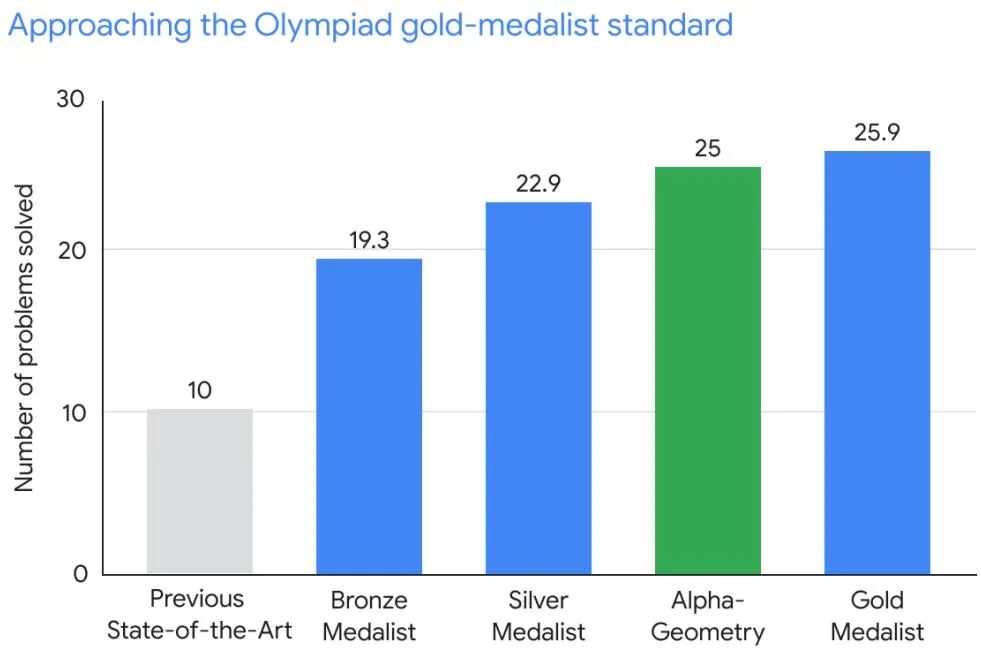
研究紹介
AlphaGeometry は、言語モデルと「記号エンジン」を組み合わせて、記号と論理規則の助けを借りて数学的推論を実行します。 その中で、言語モデルはプロセスの後続のステップの特定と予測には優れていますが、数学的推論に必要な厳密さに欠けています。一方、シンボリック エンジンは純粋に 形式論理 に基づいており、厳格なルール。これにより、言語モデルを合理的な意思決定に導くことができます。
AlphaGeometry の研究において、DeepMind は、2000 年から 2022 年にわたる 30 のオリンピック幾何学問題 (IMO-AG-30) のベンチマーク テスト セットからテストを実施しました。その結果、AlphaGeometry は競技時間中に優れたパフォーマンスを示しました。制限内の問題は 25 問。以前の最先端の方法 (Wu の方法) では、10 件しか解決できませんでした。 AI システムは、推論スキルとトレーニング データが不足しているため、幾何学や数学の複雑な問題を解決するのに苦労することがよくあることはよく知られています。 AlphaGeometry システムは、ニューラル言語モデルの予測能力とルールに制約された推論エンジンを組み合わせ、新しいソリューションを見つけるために連携します。 さらに、データの課題を解決するために、この研究では大量の合成トレーニング データ、つまり 1 億個の例が生成されました。その中で、多くの定理には証明するためのステップが 200 以上あり、これは平均より 4 ステップ長いです数学オリンピックの定理の証明長。倍。 AlphaGeometry は、論理的に推論し、新しい知識を発見して検証する AI の能力が向上していることを示しています。オリンピック レベルの幾何学問題を解決することは、AI にとって、より高度で汎用的な人工知能システムへの道を歩む重要なマイルストーンです。 フィールズ賞受賞者でIMO金メダリストのNgô Bảo Châu氏は次のように述べています。「AI研究者がなぜ最初に国際数学オリンピック(IMO)の幾何学問題を解こうとするのかが完全に理解できました。なぜなら、彼らの解法を見つけることは重要な問題だからです」これはチェスのようなもので、各手ごとに妥当な手が比較的少ないのです。しかし、彼らがこれを達成できたことには今でもショックを受けています。これは素晴らしい成果です。」
## 2010 年のフィールズ賞受賞者である呉宝珠氏は、現在シカゴ大学の教授を務めています。
AlphaGeometry は、複雑な幾何学定理の証明を見つけるために連携して動作するニューラル言語モデルと記号演繹エンジンで構成される神経記号システムです。 1 つのシステムは迅速で直感的なアイデアを提供し、もう 1 つのシステムはより思慮深く合理的な決定を提供します。
言語モデルはデータ内の一般的なパターンと関係性を識別することに優れているため、潜在的に有用な構造を迅速に予測できますが、厳密な推論や解釈が欠けていることがよくあります。一方、記号演繹エンジンは形式論理に基づいており、明示的なルールを使用して結論に達し、それらが合わせて AlphaGeometry を構成します。
AlphaGeometry の言語モデルは、その記号演繹エンジンをガイドして、幾何学的な問題に対する考えられる解決策を見つけます。一般的なオリンピックの幾何学問題は図に基づいており、解決するには点、線、円などの新しい幾何学的構造を追加する必要があります。 AlphaGeometry の言語モデルは、無数の可能性の中からどの新しい構造を追加するのが最も役立つかを予測できます。これらの手がかりはギャップを埋めるのに役立ち、シンボリック エンジンが図についてさらに推論を行い、解決策に近づくことができるようになります。
たとえば、下の図 (上) は、「ABC を AB = AC の任意の三角形とする。∠ABC = ∠BCA であることを証明せよ。」という単純な問題を AlphaGeometry で解くプロセスを示しています。
# AlphaGeometry の証明プロセスは次のようになります。AlphaGeometry は、記号演繹エンジンを実行することによって証明の検索を開始します。このエンジンは、定理の前提から開始し、定理が証明されるか新しいステートメントが使い果たされるまで、新しいステートメントを徹底的に導き出します。シンボリック エンジンが証明を見つけられなかった場合、言語モデルはシンボリック エンジンが再起動する前に証明可能な条件を追加する補助ポイントを構築します。このサイクルは、解決策が見つかるまで続きます。簡単な例では、ループは最初の補助構造「BC の中点に点 D を追加」の後で終了します。 下の図 (下) は、IMO 問題に対する AlphaGeometry のソリューションを示しています。 「三角形 FKM と KQH の外接円 (O1) と (O2) が互いに接していることを証明してください...」 AlphaGeometry はこのような複雑な問題も証明でき、証明プロセスでは補助点なども提供されます。証明は説明のために大幅に短縮および編集されています。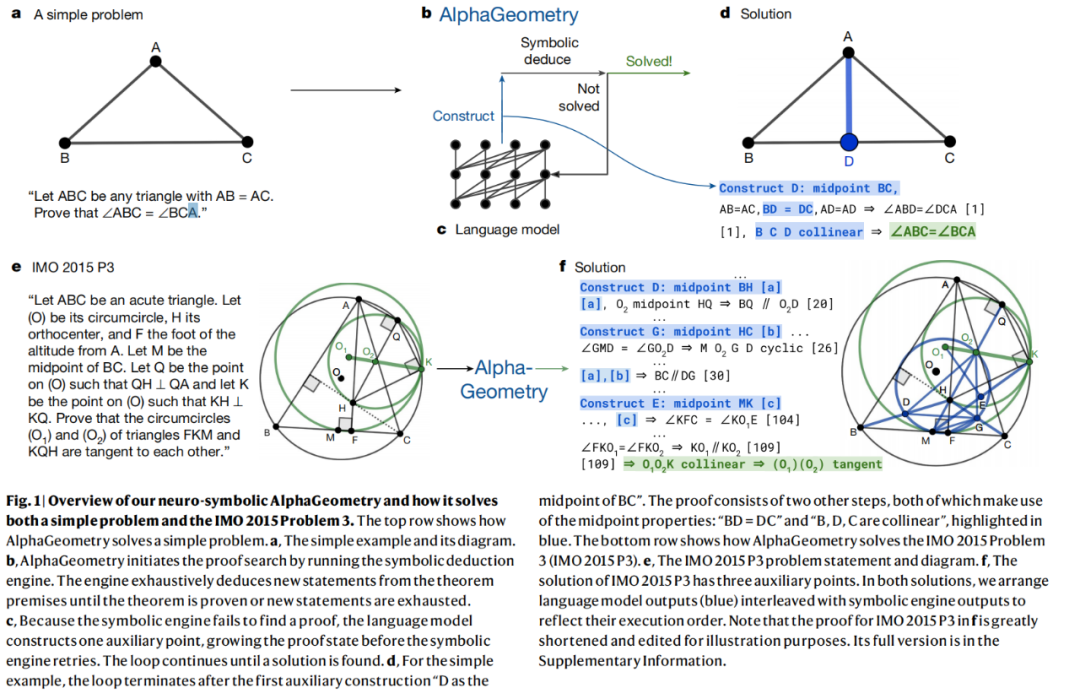
1 億件の数的推論トレーニング データを生成
人間は、紙にスケッチすることで幾何学を学習し、図を調べ、最新の Have を使用できます。新しい、より複雑な幾何学的特性と関係を発見するための知識。合成データを生成するこの研究のアプローチは、この知識構築プロセスを大規模にシミュレートします。合成データの生成方法を図 3 に示します。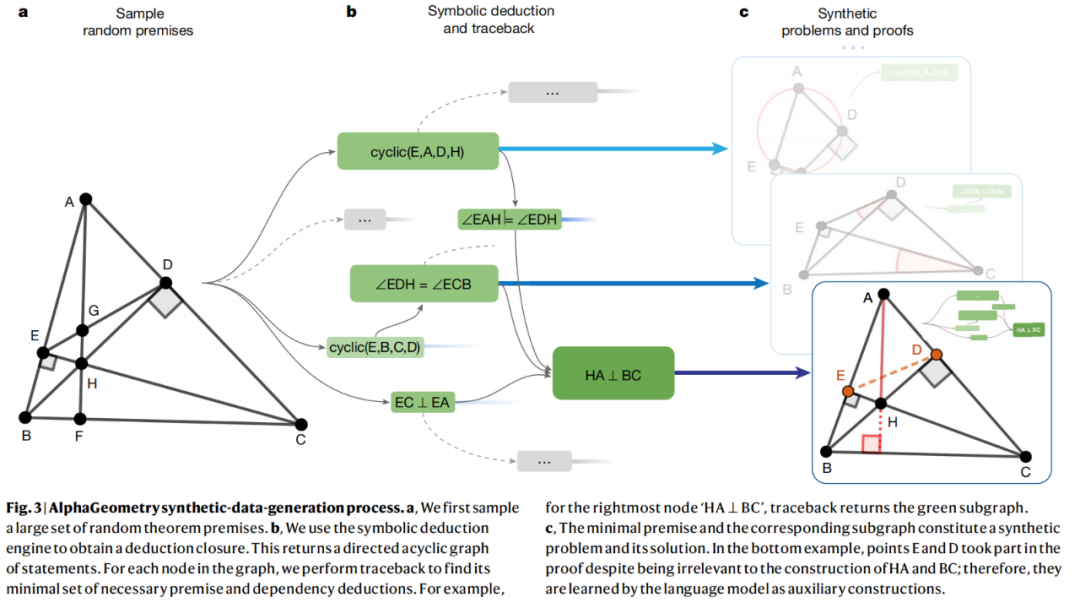
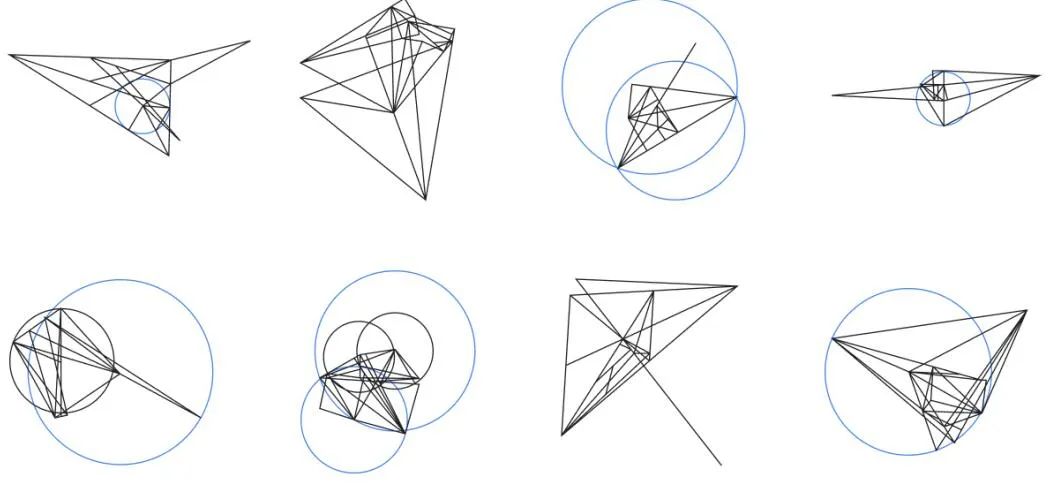
#AlphaGeometry によって生成された合成データの視覚的表現その後、この巨大なデータ プールはフィルタリングされました。同様の例を除外すると、トレーニング データセットは 1 億個になりました。
先駆的な人工知能推論機能AlphaGeometry が提供するすべてのソリューションは、コンピューターでチェックおよび検証されています。研究者らはまた、その結果を以前の人工知能手法やオリンピック競技における人間のパフォーマンスと比較しました。さらに、数学コーチで元オリンピック金メダリストの Evan Chen が、さまざまな AlphaGeometry ソリューションを評価してくれました。

MIT の数学博士候補者である Chen Yiting は、IMO 2014 金メダルを獲得しました。 Evan Chen 氏は次のように述べています。「AlphaGeometry の出力は、検証可能でクリーンであるため、印象的です。証明ベースの競争問題に対する過去の人工知能ソリューションは、時々当たり外れがありました (出力一方、AlphaGeometry にはこの弱点がありません。そのソリューションは機械で検証可能な構造を持っています。一方で、その出力は依然として人間が判読可能です。ブルートフォースによって座標系を想像することができます。幾何学の問題を解決するプログラム: 何ページにもわたる退屈な代数計算を考えてください。AlphaGeometry はそんなことはしません。人間の学生が行うような、角度や類似の三角形を含む古典的な幾何学の規則を使用します。」
最近、金融テクノロジー企業 XTX Markets は、数学的推論を実行できる人工知能モデルの開発を奨励するために、人工知能オリンピック数学賞 (AI-MO 賞) を設立しました。各オリンピックには 6 つの問題があり、通常はそのうちの 2 つだけがジオメトリに焦点を当てているため、AlphaGeometry は特定のオリンピックの問題の 3 分の 1 にしか適用できません。
これにもかかわらず、AlphaGeometry は幾何学的問題解決能力のみに依存し、2000 年と 2015 年に IMO 銅メダルの基準を突破した世界初の人工知能モデルとなりました。
DeepMind は、次世代の人工知能システムのための推論の進歩にすでに取り組んでいます。研究者らは、大規模な合成データを使用して AI システムをゼロからトレーニングする幅広い可能性を考えると、このアプローチは将来の AI システムが数学やその他の分野で新しい知識を発見する方向に影響を与える可能性があると考えています。
AlphaGeometry は、純粋な数学の美しさの探求から、言語モデルを使用した数学的および科学的問題の解決まで、人工知能における数学的推論の先駆者です。このテクノロジーは、より高度で抽象的な数学的問題を解決できるよう改良され続けることが期待されています。
AlphaGeometry の影響は、数学に加えて、コンピューター ビジョン、アーキテクチャ、さらには理論物理学などの幾何学的問題を含む、より多くの分野にも及ぶ可能性があります。
参考コンテンツ:
https://deepmind.google/discover/blog/alphageometry-an-olympiad-level-ai-system -for-geometry/
以上がディープラーニングは幾何学的推論で天才レベルのパフォーマンスを達成 Nature が DeepMind のモデルを公開し、フィールズ賞受賞ニュースで賞賛を受けるの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7364
7364
 15
15
 1628
1628
 14
14
 1353
1353
 52
52
 1265
1265
 25
25
 1214
1214
 29
29
 DeepMind ロボットが卓球をすると、フォアハンドとバックハンドが空中に滑り出し、人間の初心者を完全に打ち負かしました
Aug 09, 2024 pm 04:01 PM
DeepMind ロボットが卓球をすると、フォアハンドとバックハンドが空中に滑り出し、人間の初心者を完全に打ち負かしました
Aug 09, 2024 pm 04:01 PM
でももしかしたら公園の老人には勝てないかもしれない?パリオリンピックの真っ最中で、卓球が注目を集めています。同時に、ロボットは卓球のプレーにも新たな進歩をもたらしました。先ほど、DeepMind は、卓球競技において人間のアマチュア選手のレベルに到達できる初の学習ロボット エージェントを提案しました。論文のアドレス: https://arxiv.org/pdf/2408.03906 DeepMind ロボットは卓球でどれくらい優れていますか?おそらく人間のアマチュアプレーヤーと同等です: フォアハンドとバックハンドの両方: 相手はさまざまなプレースタイルを使用しますが、ロボットもそれに耐えることができます: さまざまなスピンでサーブを受ける: ただし、ゲームの激しさはそれほど激しくないようです公園の老人。ロボット、卓球用
 初のメカニカルクロー!元羅宝は2024年の世界ロボット会議に登場し、家庭に入ることができる初のチェスロボットを発表した
Aug 21, 2024 pm 07:33 PM
初のメカニカルクロー!元羅宝は2024年の世界ロボット会議に登場し、家庭に入ることができる初のチェスロボットを発表した
Aug 21, 2024 pm 07:33 PM
8月21日、2024年世界ロボット会議が北京で盛大に開催された。 SenseTimeのホームロボットブランド「Yuanluobot SenseRobot」は、全製品ファミリーを発表し、最近、世界初の家庭用チェスロボットとなるYuanluobot AIチェスプレイロボット - Chess Professional Edition(以下、「Yuanluobot SenseRobot」という)をリリースした。家。 Yuanluobo の 3 番目のチェス対局ロボット製品である新しい Guxiang ロボットは、AI およびエンジニアリング機械において多くの特別な技術アップグレードと革新を経て、初めて 3 次元のチェスの駒を拾う機能を実現しました。家庭用ロボットの機械的な爪を通して、チェスの対局、全員でのチェスの対局、記譜のレビューなどの人間と機械の機能を実行します。
 クロードも怠け者になってしまった!ネチズン: 自分に休日を与える方法を学びましょう
Sep 02, 2024 pm 01:56 PM
クロードも怠け者になってしまった!ネチズン: 自分に休日を与える方法を学びましょう
Sep 02, 2024 pm 01:56 PM
もうすぐ学校が始まり、新学期を迎える生徒だけでなく、大型AIモデルも気を付けなければなりません。少し前、レディットはクロードが怠け者になったと不満を漏らすネチズンでいっぱいだった。 「レベルが大幅に低下し、頻繁に停止し、出力も非常に短くなりました。リリースの最初の週は、4 ページの文書全体を一度に翻訳できましたが、今では 0.5 ページの出力さえできません」 !」 https://www.reddit.com/r/ClaudeAI/comments/1by8rw8/something_just_feels_wrong_with_claude_in_the/ というタイトルの投稿で、「クロードには完全に失望しました」という内容でいっぱいだった。
 世界ロボット会議で「未来の高齢者介護の希望」を担う家庭用ロボットを囲みました
Aug 22, 2024 pm 10:35 PM
世界ロボット会議で「未来の高齢者介護の希望」を担う家庭用ロボットを囲みました
Aug 22, 2024 pm 10:35 PM
北京で開催中の世界ロボット会議では、人型ロボットの展示が絶対的な注目となっているスターダストインテリジェントのブースでは、AIロボットアシスタントS1がダルシマー、武道、書道の3大パフォーマンスを披露した。文武両道を備えた 1 つの展示エリアには、多くの専門的な聴衆とメディアが集まりました。弾性ストリングのエレガントな演奏により、S1 は、スピード、強さ、正確さを備えた繊細な操作と絶対的なコントロールを発揮します。 CCTVニュースは、「書道」の背後にある模倣学習とインテリジェント制御に関する特別レポートを実施し、同社の創設者ライ・ジエ氏は、滑らかな動きの背後にあるハードウェア側が最高の力制御と最も人間らしい身体指標(速度、負荷)を追求していると説明した。など)、AI側では人の実際の動きのデータが収集され、強い状況に遭遇したときにロボットがより強くなり、急速に進化することを学習することができます。そしてアジャイル
 Li Feifei 氏のチームは、ロボットに空間知能を与え、GPT-4o を統合する ReKep を提案しました
Sep 03, 2024 pm 05:18 PM
Li Feifei 氏のチームは、ロボットに空間知能を与え、GPT-4o を統合する ReKep を提案しました
Sep 03, 2024 pm 05:18 PM
ビジョンとロボット学習の緊密な統合。最近話題の1X人型ロボットNEOと合わせて、2つのロボットハンドがスムーズに連携して服をたたむ、お茶を入れる、靴を詰めるといった動作をしていると、いよいよロボットの時代が到来するのではないかと感じられるかもしれません。実際、これらの滑らかな動きは、高度なロボット技術 + 精緻なフレーム設計 + マルチモーダル大型モデルの成果です。有用なロボットは多くの場合、環境との複雑かつ絶妙な相互作用を必要とし、環境は空間領域および時間領域の制約として表現できることがわかっています。たとえば、ロボットにお茶を注いでもらいたい場合、ロボットはまずティーポットのハンドルを掴んで、お茶をこぼさないように垂直に保ち、次にポットの口がカップの口と揃うまでスムーズに動かす必要があります。 、そしてティーポットを一定の角度に傾けます。これ
 ACL 2024 賞の発表: HuaTech による Oracle 解読に関する最優秀論文の 1 つ、GloVe Time Test Award
Aug 15, 2024 pm 04:37 PM
ACL 2024 賞の発表: HuaTech による Oracle 解読に関する最優秀論文の 1 つ、GloVe Time Test Award
Aug 15, 2024 pm 04:37 PM
貢献者はこの ACL カンファレンスから多くのことを学びました。 6日間のACL2024がタイのバンコクで開催されています。 ACL は、計算言語学と自然言語処理の分野におけるトップの国際会議で、国際計算言語学協会が主催し、毎年開催されます。 ACL は NLP 分野における学術的影響力において常に第一位にランクされており、CCF-A 推奨会議でもあります。今年の ACL カンファレンスは 62 回目であり、NLP 分野における 400 以上の最先端の作品が寄せられました。昨日の午後、カンファレンスは最優秀論文およびその他の賞を発表しました。今回の優秀論文賞は7件(未発表2件)、最優秀テーマ論文賞1件、優秀論文賞35件です。このカンファレンスでは、3 つの Resource Paper Award (ResourceAward) と Social Impact Award (
 宏蒙スマートトラベルS9とフルシナリオ新製品発売カンファレンス、多数の大ヒット新製品が一緒にリリースされました
Aug 08, 2024 am 07:02 AM
宏蒙スマートトラベルS9とフルシナリオ新製品発売カンファレンス、多数の大ヒット新製品が一緒にリリースされました
Aug 08, 2024 am 07:02 AM
今日の午後、Hongmeng Zhixingは新しいブランドと新車を正式に歓迎しました。 8月6日、ファーウェイはHongmeng Smart Xingxing S9およびファーウェイのフルシナリオ新製品発表カンファレンスを開催し、パノラマスマートフラッグシップセダンXiangjie S9、新しいM7ProおよびHuawei novaFlip、MatePad Pro 12.2インチ、新しいMatePad Air、Huawei Bisheng Withを発表しました。レーザー プリンタ X1 シリーズ、FreeBuds6i、WATCHFIT3、スマート スクリーン S5Pro など、スマート トラベル、スマート オフィスからスマート ウェアに至るまで、多くの新しいオールシナリオ スマート製品を開発し、ファーウェイは消費者にスマートな体験を提供するフル シナリオのスマート エコシステムを構築し続けています。すべてのインターネット。宏孟志興氏:スマートカー業界のアップグレードを促進するための徹底的な権限付与 ファーウェイは中国の自動車業界パートナーと提携して、
 中国初の大型UIモデル登場! Motiff の大規模モデルはデザイナーにとって最適なアシスタントを作成し、UI デザインのワークフローを最適化します
Aug 19, 2024 pm 04:48 PM
中国初の大型UIモデル登場! Motiff の大規模モデルはデザイナーにとって最適なアシスタントを作成し、UI デザインのワークフローを最適化します
Aug 19, 2024 pm 04:48 PM
人工知能は想像を超えるスピードで発展しています。 GPT-4 がマルチモーダル技術を一般に公開して以来、マルチモーダル大型モデルは急速な開発段階に入り、純粋なモデルの研究開発から垂直分野での探査と応用へと徐々に移行し、あらゆる分野に深く統合されています。インターフェイス インタラクションの分野では、Google や Apple などの国際的なテクノロジー大手が、携帯電話 AI 革命を前進させる唯一の方法とみなされている大規模なマルチモーダル UI モデルの研究開発に投資してきました。このような状況の中で、中国初の大規模UIモデルが誕生しました。 8月17日、国際エクスペリエンスデザインカンファレンス「IXDC2024」において、AI時代のデザインツールであるMotiffは、独自開発したUIマルチモーダルモデル「Motiff Model」を発表した。世界初のUIデザインツールです



