関数 fx をベクトル a ベクトル b ベクトル c とします。ここで、ベクトル a

関数 fx ベクトル a ベクトル b ベクトル c ベクトル a sinx と仮定します。
ベクトル d(h,k)
と仮定します。つまり、x'=x-h; y'=y-k
x=x'-h ; y=y'-k
次に、上記の式を元の F(x) に代入します。
y'-h=2 √2sin(2x-2h-3π/4)を取得しますここで、質問文中の「平行移動後の画像を座標原点の中心に対して対称にする」という条件を見てみましょう。
つまり、x=0 の場合、最初の変換後の方程式 g(0)=0
つまり、この時点では -2h-3π/4=kπ
の h=3π/8-kπ/2
そうすると、d(3π/8-kπ/2,-2)
が得られます。この質問に答える鍵は、変換方法に従ってベクトルを設定することです
これは x'=x-h; y'=y-k
x=x'-h ; y=y'-k
f(x)=ベクトル a*(b c)
質問から f(x)=(sinx,-cosx)*(sinx-cosx,-3cosx sinx)
f(x)=sinx(sinx-cosx)-cosx(-3cosx sinx)
=sinxsinx-sinxcosx 3cosxcosx-sinxcosx
=sinxsins 3cosxcosx-2sinxcosx
=sinxsinx cosxcosx 2cosxcosx-2sinxcosx
=cos2x-sin2x
=平方根 2/2 sin(2x 45 度)
関数 fx ベクトル a ベクトル b c と仮定します。 ここで、ベクトル a sinx cosx ベクトル b sinx
(1)f(x)=a(b c)=ab ac=sinxsinx 3coxcox-2sinxcosxxx
=2cosxcosx-sin2x 1
=-sin2x cos2x 2
=√2sin(2x 3π/4) 2
(2) x が [3π/8, 7π/8] に属する場合、2x 3π/4 は [3π/2, 5π/2] に属します。
sinx の性質によれば、f(x) は [3π/8,7π/8] で単調増加します。(3) まず y=cosx を π/2 単位右に変換して、y=cos(x-π/2)=sinx
を取得します。x が変化せず、y が √2 倍に増加すると、y=√2sinx
が得られます。y が変更されない場合、x は元の値の 1/2 に減らされ、y=√2sin(2x)
左に 3π/8 単位移動して、y=√2sin(2x 3π/4) を取得します。
最後に 2 単位上方に変換して、y=√2sin(2x 3π/4) 2を取得します。
以上が関数 fx をベクトル a ベクトル b ベクトル c とします。ここで、ベクトル aの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7467
7467
 15
15
 1376
1376
 52
52
 77
77
 11
11
 18
18
 20
20
 レジストリを編集するにはどうすればよいですか? (警告:注意して使用してください!)
Mar 21, 2025 pm 07:46 PM
レジストリを編集するにはどうすればよいですか? (警告:注意して使用してください!)
Mar 21, 2025 pm 07:46 PM
記事では、誤った編集からWindowsレジストリ、予防策、バックアップ方法、潜在的な問題の編集について説明します。主な問題:システムの不安定性と不適切な変化によるデータ損失のリスク。
 Windows設定でドライブヘルス警告を修正する方法を発見する
Mar 19, 2025 am 11:10 AM
Windows設定でドライブヘルス警告を修正する方法を発見する
Mar 19, 2025 am 11:10 AM
Windowsの設定でのドライブヘルス警告はどういう意味ですか?ディスク警告を受け取ったときに何をすべきですか?このPHP.CNチュートリアルを読んで、この状況に対処するための段階的な指示を取得してください。
 Windowsでサービスを管理するにはどうすればよいですか?
Mar 21, 2025 pm 07:52 PM
Windowsでサービスを管理するにはどうすればよいですか?
Mar 21, 2025 pm 07:52 PM
記事では、システムの健康のためのWindowsサービスの管理、開始、停止、サービスの再起動、安定性のためのベストプラクティスなどについて説明します。
 どのアプリケーションがENE.SYSを使用していますか
Mar 12, 2025 pm 01:25 PM
どのアプリケーションがENE.SYSを使用していますか
Mar 12, 2025 pm 01:25 PM
この記事では、ENE.SYSがRealTekの高解像度オーディオドライバーコンポーネントとして識別します。 オーディオハードウェアの管理における機能を詳しく説明し、オーディオ機能における重要な役割を強調しています。 また、この記事は、ユーザーの正当性の確認についてもガイドしています
 グループポリシーエディター(gpedit.msc)を使用するにはどうすればよいですか?
Mar 21, 2025 pm 07:48 PM
グループポリシーエディター(gpedit.msc)を使用するにはどうすればよいですか?
Mar 21, 2025 pm 07:48 PM
この記事では、システム設定を管理するためにWindowsでグループポリシーエディター(gpedit.msc)を使用する方法、一般的な構成とトラブルシューティング方法を強調する方法について説明します。 Gpedit.mscはWindows Home Editionsでは利用できないことに注意してください。
 ファイルタイプのデフォルトアプリを変更するにはどうすればよいですか?
Mar 21, 2025 pm 07:48 PM
ファイルタイプのデフォルトアプリを変更するにはどうすればよいですか?
Mar 21, 2025 pm 07:48 PM
記事では、リターンやバルクの変更など、ウィンドウ上のファイルタイプのデフォルトアプリの変更について説明します。主な問題:組み込みのバルク変更オプションはありません。
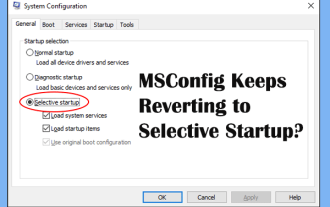 msconfigは選択的なスタートアップに戻り続けますか?ここで2つのソリューション
Mar 28, 2025 pm 12:06 PM
msconfigは選択的なスタートアップに戻り続けますか?ここで2つのソリューション
Mar 28, 2025 pm 12:06 PM
MsconfigがWindowsの選択的な起動に戻っているという問題について質問されていますか?必要な場合は、通常のスタートアップに切り替える方法は?このphp.cn投稿で説明されている方法を試して、あなたに合ったものを見つけてください。
 Windowsメタデータとインターネットサービスの問題:修正方法は?
Apr 02, 2025 pm 03:57 PM
Windowsメタデータとインターネットサービスの問題:修正方法は?
Apr 02, 2025 pm 03:57 PM
「Windowsメタデータとインターネットサービス(WMIS)への接続が確立できなかった」が表示される場合があります。イベントビューアのエラー。 PHP.CNからのこの投稿では、Windowsメタデータとインターネットサービスの問題を削除する方法を紹介します。




