OLS回帰の定義と応用

通常最小二乗法 (OLS) 回帰は、線形回帰モデル内のデータ ポイントに最も近い直線を見つけるように設計された最適化戦略です。 OLS は、アルファとベータの不偏推定値を提供できるため、線形回帰モデルで最も効果的な最適化手法として広く認識されています。残差の二乗和を最小化することで、OLS は回帰直線がデータ ポイントに最も高い適合度を持つように最適なパラメーター値を見つけることができます。この方法は、独立変数と従属変数の間の関係を理解するのに役立つだけでなく、予測分析と推論分析も可能にします。全体として、OLS 回帰は、説明と予測に役立つシンプルかつ強力なツールです。
OLS を線形回帰に適用する方法
線形回帰は、タスクの教師あり機械学習アルゴリズムで使用される手法です。 。これは主に分類問題ではなく回帰問題に適用されます。回帰問題には連続値の予測が含まれますが、分類問題にはカテゴリの予測が含まれます。したがって、線形回帰アルゴリズムの目標は、線形モデルを構築して連続ターゲット変数を予測することです。分類とは異なり、ターゲット変数はカテゴリ値ではなく、数値または連続値です。線形回帰アルゴリズムを通じて、入力変数の線形関係に基づいて連続数を予測し、問題をモデル化して予測できます。
回帰タスクは 2 つのカテゴリに分類できます。1 つは 1 つの特徴のみを使用してターゲットを予測するタスク、もう 1 つは複数の特徴を使用してターゲットを予測するタスクです。
線形回帰モデルで OLS を見つける方法
単純な線形回帰の目標は、パラメーターを調整して誤差項を最小限に抑えることです。具体的には、モデルは二乗誤差の最小化を最適化目標として採用します。正の誤差と負の誤差が互いに打ち消し合うことは望ましくありません。両方ともモデルにペナルティを与えることになるからです。したがって、このプロセスは通常最小二乗 (OLS) 誤差と呼ばれます。
要約すると、OLS はデータ ポイントの直線を当てはめるために使用される最適化戦略です。 OLS は唯一の最適化戦略ではありませんが、アルファとベータの実際の値の不偏推定値を提供するため、最も人気のある戦略の 1 つです。
ガウス-マルコフの定理と線形回帰モデルの仮定によれば、OLS 推定器はパラメーターの線形性、観測値のランダム サンプリング、ゼロ条件付き平均、多重共線性なし、誤差等分散性に基づいています。最良の不偏線形推定器と考えられています。
以上がOLS回帰の定義と応用の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7467
7467
 15
15
 1376
1376
 52
52
 77
77
 11
11
 19
19
 20
20
 Bytedance Cutting が SVIP スーパー メンバーシップを開始: 継続的な年間サブスクリプションは 499 元で、さまざまな AI 機能を提供
Jun 28, 2024 am 03:51 AM
Bytedance Cutting が SVIP スーパー メンバーシップを開始: 継続的な年間サブスクリプションは 499 元で、さまざまな AI 機能を提供
Jun 28, 2024 am 03:51 AM
このサイトは6月27日、JianyingはByteDanceの子会社であるFaceMeng Technologyによって開発されたビデオ編集ソフトウェアであり、Douyinプラットフォームに依存しており、基本的にプラットフォームのユーザー向けに短いビデオコンテンツを作成すると報告しました。 Windows、MacOS、その他のオペレーティング システム。 Jianyingは会員システムのアップグレードを正式に発表し、インテリジェント翻訳、インテリジェントハイライト、インテリジェントパッケージング、デジタルヒューマン合成などのさまざまなAIブラックテクノロジーを含む新しいSVIPを開始しました。価格的には、クリッピングSVIPの月額料金は79元、年会費は599元(当サイト注:月額49.9元に相当)、継続月額サブスクリプションは月額59元、継続年間サブスクリプションは、年間499元(月額41.6元に相当)です。さらに、カット担当者は、ユーザーエクスペリエンスを向上させるために、オリジナルのVIPに登録している人は、
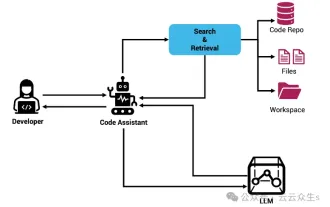 Rag と Sem-Rag を使用したコンテキスト拡張 AI コーディング アシスタント
Jun 10, 2024 am 11:08 AM
Rag と Sem-Rag を使用したコンテキスト拡張 AI コーディング アシスタント
Jun 10, 2024 am 11:08 AM
検索強化生成およびセマンティック メモリを AI コーディング アシスタントに組み込むことで、開発者の生産性、効率、精度を向上させます。 JanakiramMSV 著者の EnhancingAICodingAssistantswithContextUsingRAGandSEM-RAG から翻訳。基本的な AI プログラミング アシスタントは当然役に立ちますが、ソフトウェア言語とソフトウェア作成の最も一般的なパターンに関する一般的な理解に依存しているため、最も適切で正しいコードの提案を提供できないことがよくあります。これらのコーディング アシスタントによって生成されたコードは、彼らが解決する責任を負っている問題の解決には適していますが、多くの場合、個々のチームのコーディング標準、規約、スタイルには準拠していません。これにより、コードがアプリケーションに受け入れられるように修正または調整する必要がある提案が得られることがよくあります。
 GenAI および LLM の技術面接に関する 7 つのクールな質問
Jun 07, 2024 am 10:06 AM
GenAI および LLM の技術面接に関する 7 つのクールな質問
Jun 07, 2024 am 10:06 AM
AIGC について詳しくは、51CTOAI.x コミュニティ https://www.51cto.com/aigc/Translator|Jingyan Reviewer|Chonglou を参照してください。これらの質問は、インターネット上のどこでも見られる従来の質問バンクとは異なります。既成概念にとらわれずに考える必要があります。大規模言語モデル (LLM) は、データ サイエンス、生成人工知能 (GenAI)、および人工知能の分野でますます重要になっています。これらの複雑なアルゴリズムは人間のスキルを向上させ、多くの業界で効率とイノベーションを推進し、企業が競争力を維持するための鍵となります。 LLM は、自然言語処理、テキスト生成、音声認識、推奨システムなどの分野で幅広い用途に使用できます。 LLM は大量のデータから学習することでテキストを生成できます。
 微調整によって本当に LLM が新しいことを学習できるようになるのでしょうか: 新しい知識を導入すると、モデルがより多くの幻覚を生成する可能性があります
Jun 11, 2024 pm 03:57 PM
微調整によって本当に LLM が新しいことを学習できるようになるのでしょうか: 新しい知識を導入すると、モデルがより多くの幻覚を生成する可能性があります
Jun 11, 2024 pm 03:57 PM
大規模言語モデル (LLM) は巨大なテキスト データベースでトレーニングされ、そこで大量の現実世界の知識を取得します。この知識はパラメータに組み込まれており、必要なときに使用できます。これらのモデルの知識は、トレーニングの終了時に「具体化」されます。事前トレーニングの終了時に、モデルは実際に学習を停止します。モデルを調整または微調整して、この知識を活用し、ユーザーの質問により自然に応答する方法を学びます。ただし、モデルの知識だけでは不十分な場合があり、モデルは RAG を通じて外部コンテンツにアクセスできますが、微調整を通じてモデルを新しいドメインに適応させることが有益であると考えられます。この微調整は、ヒューマン アノテーターまたは他の LLM 作成物からの入力を使用して実行され、モデルは追加の実世界の知識に遭遇し、それを統合します。
 新しい科学的で複雑な質問応答ベンチマークと大規模モデルの評価システムを提供するために、UNSW、アルゴンヌ、シカゴ大学、およびその他の機関が共同で SciQAG フレームワークを立ち上げました。
Jul 25, 2024 am 06:42 AM
新しい科学的で複雑な質問応答ベンチマークと大規模モデルの評価システムを提供するために、UNSW、アルゴンヌ、シカゴ大学、およびその他の機関が共同で SciQAG フレームワークを立ち上げました。
Jul 25, 2024 am 06:42 AM
編集者 |ScienceAI 質問応答 (QA) データセットは、自然言語処理 (NLP) 研究を促進する上で重要な役割を果たします。高品質の QA データ セットは、モデルの微調整に使用できるだけでなく、大規模言語モデル (LLM) の機能、特に科学的知識を理解し推論する能力を効果的に評価することもできます。現在、医学、化学、生物学、その他の分野をカバーする多くの科学 QA データ セットがありますが、これらのデータ セットにはまだいくつかの欠点があります。まず、データ形式は比較的単純で、そのほとんどが多肢選択式の質問であり、評価は簡単ですが、モデルの回答選択範囲が制限され、科学的な質問に回答するモデルの能力を完全にテストすることはできません。対照的に、自由回答型の Q&A
 あなたが知らない機械学習の 5 つの流派
Jun 05, 2024 pm 08:51 PM
あなたが知らない機械学習の 5 つの流派
Jun 05, 2024 pm 08:51 PM
機械学習は人工知能の重要な分野であり、明示的にプログラムしなくてもコンピューターにデータから学習して能力を向上させる機能を提供します。機械学習は、画像認識や自然言語処理から、レコメンデーションシステムや不正行為検出に至るまで、さまざまな分野で幅広く応用されており、私たちの生活様式を変えつつあります。機械学習の分野にはさまざまな手法や理論があり、その中で最も影響力のある 5 つの手法は「機械学習の 5 つの流派」と呼ばれています。 5 つの主要な学派は、象徴学派、コネクショニスト学派、進化学派、ベイジアン学派、およびアナロジー学派です。 1. 象徴主義は、象徴主義とも呼ばれ、論理的推論と知識の表現のためのシンボルの使用を強調します。この学派は、学習は既存の既存の要素を介した逆演繹のプロセスであると信じています。
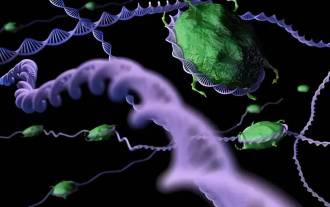 SOTA パフォーマンス、厦門マルチモーダルタンパク質-リガンド親和性予測 AI 手法、初めて分子表面情報を結合
Jul 17, 2024 pm 06:37 PM
SOTA パフォーマンス、厦門マルチモーダルタンパク質-リガンド親和性予測 AI 手法、初めて分子表面情報を結合
Jul 17, 2024 pm 06:37 PM
編集者 | KX 医薬品の研究開発の分野では、タンパク質とリガンドの結合親和性を正確かつ効果的に予測することが、医薬品のスクリーニングと最適化にとって重要です。しかし、現在の研究では、タンパク質とリガンドの相互作用における分子表面情報の重要な役割が考慮されていません。これに基づいて、アモイ大学の研究者らは、初めてタンパク質の表面、3D 構造、配列に関する情報を組み合わせ、クロスアテンション メカニズムを使用して異なるモダリティの特徴を比較する、新しいマルチモーダル特徴抽出 (MFE) フレームワークを提案しました。アライメント。実験結果は、この方法がタンパク質-リガンド結合親和性の予測において最先端の性能を達成することを実証しています。さらに、アブレーション研究は、この枠組み内でのタンパク質表面情報と多峰性特徴の位置合わせの有効性と必要性を実証しています。 「S」で始まる関連研究
 AIなどの市場を開拓するグローバルファウンドリーズがタゴール・テクノロジーの窒化ガリウム技術と関連チームを買収
Jul 15, 2024 pm 12:21 PM
AIなどの市場を開拓するグローバルファウンドリーズがタゴール・テクノロジーの窒化ガリウム技術と関連チームを買収
Jul 15, 2024 pm 12:21 PM
7月5日のこのウェブサイトのニュースによると、グローバルファウンドリーズは今年7月1日にプレスリリースを発行し、自動車とインターネットでの市場シェア拡大を目指してタゴール・テクノロジーのパワー窒化ガリウム(GaN)技術と知的財産ポートフォリオを買収したことを発表した。モノと人工知能データセンターのアプリケーション分野で、より高い効率とより優れたパフォーマンスを探求します。生成 AI などのテクノロジーがデジタル世界で発展を続ける中、窒化ガリウム (GaN) は、特にデータセンターにおいて、持続可能で効率的な電力管理のための重要なソリューションとなっています。このウェブサイトは、この買収中にタゴール・テクノロジーのエンジニアリングチームがGLOBALFOUNDRIESに加わり、窒化ガリウム技術をさらに開発するという公式発表を引用した。 G




