任意の連続単一値関数は、単層ニューラル ネットワークで近似できます。

単層ニューラル ネットワークはパーセプトロンとも呼ばれ、最も単純なニューラル ネットワーク構造です。これは入力層と出力層で構成され、各入力と出力の間に重み付けされた接続が含まれます。その主な目的は、入力と出力の間のマッピング関係を学習することです。単層ニューラル ネットワークは、その強力な近似能力により、さまざまな単一値連続関数に適合できます。したがって、パターン認識および予測問題に幅広く応用できる可能性があります。
単層ニューラル ネットワークの近似能力は、パーセプトロンの収束定理によって証明できます。この定理は、パーセプトロンは線形分離可能な関数を 2 つのカテゴリに分離するインターフェースを見つけることができると述べています。これは、パーセプトロンの線形近似機能を示しています。ただし、非線形関数の場合、単層ニューラル ネットワークの近似能力には限界があります。したがって、非線形関数を処理するには、多層ニューラル ネットワークまたはその他のより複雑なモデルを使用する必要があります。これらのモデルはより強力な近似機能を備えており、非線形関係をより適切に処理できます。
幸いなことに、シグモイド関数を活性化関数として使用して、単層ニューラル ネットワークの近似機能を拡張できます。シグモイド関数は、実数を 0 から 1 までの値にマッピングする、一般的に使用される非線形関数です。シグモイド関数を単層ニューラル ネットワークの活性化関数として使用することで、非線形近似機能を備えたニューラル ネットワークを構築できます。これは、シグモイド関数が入力データを非線形空間にマッピングできるため、ニューラル ネットワークが非線形関数を近似できるためです。活性化関数としてシグモイド関数を使用する利点は、滑らかな特性を持ち、ニューラル ネットワークの出力値の激しい変動を回避できることです。また、シグモイド関数は計算が比較的簡単であり、効率的に計算することができる。したがって、シグモイド関数は、単層ニューラル ネットワークの近似能力を拡張するのに適した、一般的に使用される効果的な活性化関数です。
シグモイド関数に加えて、ReLU 関数と Tanh 関数もよく使われる活性化関数であり、いずれも非線形特性を持ち、単層ニューラルの近似能力を高めることができます。通信網。
ただし、非常に複雑な関数の場合は、単層ニューラル ネットワークに適合させるために多数のニューロンが必要になる場合があります。このため、複雑な問題を扱う場合、単層ニューラル ネットワークの適用性が制限されます。単層ニューラル ネットワークでは、これらの問題に対処するために多数のニューロンが必要になることが多く、過剰適合や過度の計算負荷につながる可能性があるためです。
この問題を解決するには、多層ニューラル ネットワークを使用できます。多層ニューラル ネットワークは、複数のニューロンで構成されるニューラル ネットワークであり、各ニューロンは独自の活性化関数と重みを持ちます。多層ニューラル ネットワークには通常、入力層、隠れ層、出力層が含まれます。隠れ層は、入力層と出力層の間に位置する 1 つ以上のニューロン層です。隠れ層はニューラル ネットワークの近似能力を高め、非線形問題を効果的に処理できます。
多層ニューラル ネットワークを使用すると、単層ニューラル ネットワークでは処理できない複雑な問題を効果的に解決できます。多層ニューラル ネットワークは、隠れ層を追加することで近似機能を拡張できます。隠れ層の各ニューロンは、目的関数をより適切に近似するために使用できる特定の特徴やパターンを学習できます。さらに、多層ニューラル ネットワークでは、バックプロパゲーション アルゴリズムを使用してニューロン間の重みを調整し、誤差を最小限に抑え、予測精度を向上させることもできます。
つまり、単層ニューラル ネットワークは任意の単一値連続関数に適合しますが、非線形関数や非常に複雑な問題の場合、単層ニューラル ネットワークの近似能力は限界がある可能性があります。十分ではありません。多層ニューラル ネットワークを使用すると、これらの問題に効果的に対処でき、ニューラル ネットワークの近似能力と予測精度が向上します。
以上が任意の連続単一値関数は、単層ニューラル ネットワークで近似できます。の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7486
7486
 15
15
 1377
1377
 52
52
 77
77
 11
11
 19
19
 38
38
 RNN、LSTM、GRU の概念、違い、長所と短所を調べる
Jan 22, 2024 pm 07:51 PM
RNN、LSTM、GRU の概念、違い、長所と短所を調べる
Jan 22, 2024 pm 07:51 PM
時系列データでは、観測間に依存関係があるため、相互に独立していません。ただし、従来のニューラル ネットワークは各観測値を独立したものとして扱うため、時系列データをモデル化するモデルの能力が制限されます。この問題を解決するために、リカレント ニューラル ネットワーク (RNN) が導入されました。これは、ネットワーク内のデータ ポイント間の依存関係を確立することにより、時系列データの動的特性をキャプチャするためのメモリの概念を導入しました。反復接続を通じて、RNN は以前の情報を現在の観測値に渡して、将来の値をより適切に予測できます。このため、RNN は時系列データを含むタスクにとって強力なツールになります。しかし、RNN はどのようにしてこの種の記憶を実現するのでしょうか? RNN は、ニューラル ネットワーク内のフィードバック ループを通じて記憶を実現します。これが RNN と従来のニューラル ネットワークの違いです。
 ニューラル ネットワークの浮動小数点オペランド (FLOPS) の計算
Jan 22, 2024 pm 07:21 PM
ニューラル ネットワークの浮動小数点オペランド (FLOPS) の計算
Jan 22, 2024 pm 07:21 PM
FLOPS はコンピュータの性能評価の規格の 1 つで、1 秒あたりの浮動小数点演算の回数を測定するために使用されます。ニューラル ネットワークでは、モデルの計算の複雑さとコンピューティング リソースの使用率を評価するために FLOPS がよく使用されます。これは、コンピューターの計算能力と効率を測定するために使用される重要な指標です。ニューラル ネットワークは、データ分類、回帰、クラスタリングなどのタスクを実行するために使用される、複数のニューロン層で構成される複雑なモデルです。ニューラル ネットワークのトレーニングと推論には、多数の行列の乗算、畳み込み、その他の計算操作が必要となるため、計算の複雑さは非常に高くなります。 FLOPS (FloatingPointOperationsperSecond) を使用すると、ニューラル ネットワークの計算の複雑さを測定し、モデルの計算リソースの使用効率を評価できます。フロップ
 テキスト分類に双方向 LSTM モデルを使用するケーススタディ
Jan 24, 2024 am 10:36 AM
テキスト分類に双方向 LSTM モデルを使用するケーススタディ
Jan 24, 2024 am 10:36 AM
双方向 LSTM モデルは、テキスト分類に使用されるニューラル ネットワークです。以下は、テキスト分類タスクに双方向 LSTM を使用する方法を示す簡単な例です。まず、必要なライブラリとモジュールをインポートする必要があります: importosimportnumpyasnpfromkeras.preprocessing.textimportTokenizerfromkeras.preprocessing.sequenceimportpad_sequencesfromkeras.modelsimportSequentialfromkeras.layersimportDense,Em
 ファジーニューラルネットワークの定義と構造解析
Jan 22, 2024 pm 09:09 PM
ファジーニューラルネットワークの定義と構造解析
Jan 22, 2024 pm 09:09 PM
ファジー ニューラル ネットワークは、ファジー ロジックとニューラル ネットワークを組み合わせたハイブリッド モデルで、従来のニューラル ネットワークでは処理が困難なファジーまたは不確実な問題を解決します。その設計は人間の認知における曖昧さと不確実性にインスピレーションを得ているため、制御システム、パターン認識、データマイニングなどの分野で広く使用されています。ファジー ニューラル ネットワークの基本アーキテクチャは、ファジー サブシステムとニューラル サブシステムで構成されます。ファジー サブシステムは、ファジー ロジックを使用して入力データを処理し、それをファジー セットに変換して、入力データの曖昧さと不確実性を表現します。ニューラル サブシステムは、ニューラル ネットワークを使用して、分類、回帰、クラスタリングなどのタスクのファジー セットを処理します。ファジー サブシステムとニューラル サブシステム間の相互作用により、ファジー ニューラル ネットワークはより強力な処理能力を持ち、
 畳み込みニューラル ネットワークを使用した画像のノイズ除去
Jan 23, 2024 pm 11:48 PM
畳み込みニューラル ネットワークを使用した画像のノイズ除去
Jan 23, 2024 pm 11:48 PM
畳み込みニューラル ネットワークは、画像のノイズ除去タスクで優れたパフォーマンスを発揮します。学習したフィルターを利用してノイズを除去し、元の画像を復元します。この記事では、畳み込みニューラル ネットワークに基づく画像ノイズ除去方法を詳しく紹介します。 1. 畳み込みニューラル ネットワークの概要 畳み込みニューラル ネットワークは、複数の畳み込み層、プーリング層、全結合層の組み合わせを使用して画像の特徴を学習および分類する深層学習アルゴリズムです。畳み込み層では、畳み込み演算を通じて画像の局所的な特徴が抽出され、それによって画像内の空間相関が捕捉されます。プーリング層は、特徴の次元を削減することで計算量を削減し、主要な特徴を保持します。完全に接続された層は、学習した特徴とラベルをマッピングして画像分類やその他のタスクを実装する役割を果たします。このネットワーク構造の設計により、畳み込みニューラル ネットワークは画像処理と認識に役立ちます。
 SqueezeNet の概要とその特徴
Jan 22, 2024 pm 07:15 PM
SqueezeNet の概要とその特徴
Jan 22, 2024 pm 07:15 PM
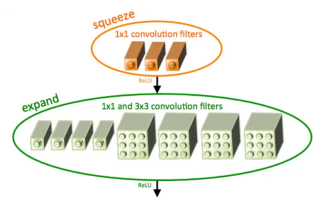
SqueezeNet は、高精度と低複雑性のバランスが取れた小型で正確なアルゴリズムであり、リソースが限られているモバイル システムや組み込みシステムに最適です。 2016 年、DeepScale、カリフォルニア大学バークレー校、スタンフォード大学の研究者は、コンパクトで効率的な畳み込みニューラル ネットワーク (CNN) である SqueezeNet を提案しました。近年、研究者は SqueezeNetv1.1 や SqueezeNetv2.0 など、SqueezeNet にいくつかの改良を加えました。両方のバージョンの改良により、精度が向上するだけでなく、計算コストも削減されます。 ImageNet データセット上の SqueezeNetv1.1 の精度
 ツイン ニューラル ネットワーク: 原理と応用分析
Jan 24, 2024 pm 04:18 PM
ツイン ニューラル ネットワーク: 原理と応用分析
Jan 24, 2024 pm 04:18 PM
シャム ニューラル ネットワークは、ユニークな人工ニューラル ネットワーク構造です。これは、同じパラメーターと重みを共有する 2 つの同一のニューラル ネットワークで構成されます。同時に、2 つのネットワークは同じ入力データも共有します。 2 つのニューラル ネットワークは構造的に同一であるため、このデザインは双子からインスピレーションを得ています。シャム ニューラル ネットワークの原理は、2 つの入力データ間の類似性や距離を比較することによって、画像マッチング、テキスト マッチング、顔認識などの特定のタスクを完了することです。トレーニング中、ネットワークは、類似したデータを隣接する領域にマッピングし、異なるデータを離れた領域にマッピングしようとします。このようにして、ネットワークはさまざまなデータを分類または照合する方法を学習して、対応するデータを実現できます。
 因果畳み込みニューラル ネットワーク
Jan 24, 2024 pm 12:42 PM
因果畳み込みニューラル ネットワーク
Jan 24, 2024 pm 12:42 PM
因果畳み込みニューラル ネットワークは、時系列データの因果関係の問題のために設計された特別な畳み込みニューラル ネットワークです。従来の畳み込みニューラル ネットワークと比較して、因果畳み込みニューラル ネットワークは、時系列の因果関係を保持するという独特の利点があり、時系列データの予測と分析に広く使用されています。因果畳み込みニューラル ネットワークの中心的なアイデアは、畳み込み演算に因果関係を導入することです。従来の畳み込みニューラルネットワークは、現時点の前後のデータを同時に認識できますが、時系列予測では情報漏洩の問題が発生する可能性があります。現時点での予測結果は、将来の時点のデータに影響を受けるからです。この問題を解決するのが因果畳み込みニューラル ネットワークであり、現時点と過去のデータのみを認識することができ、将来のデータを認識することはできません。




