
二叉树是一种树状数据结构,其中每个父节点最多可以有两个子节点。
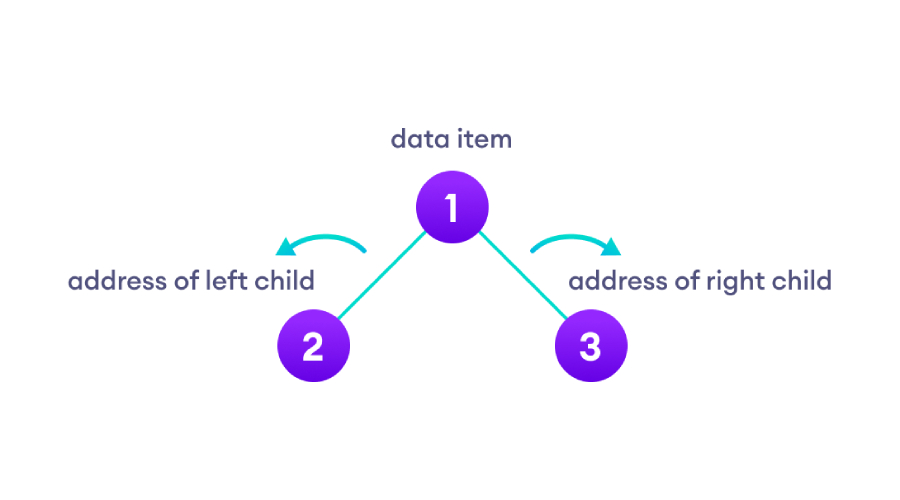
完全二叉树是一种特殊类型的二叉树,其父节点存在2种情况,要么有2个子节点,要么没有子节点,详情如下图:
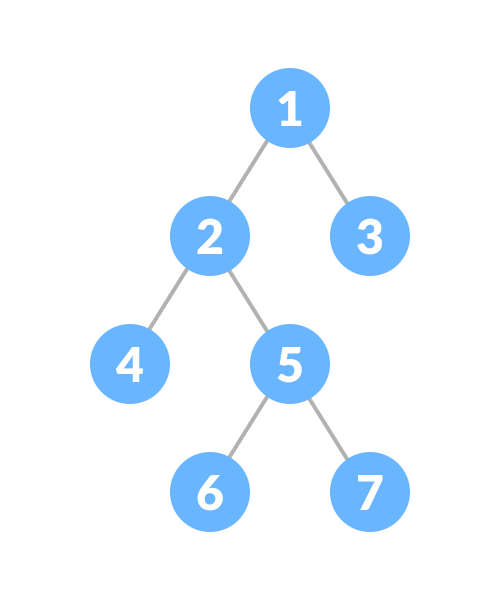
1、叶数为i+1
2、节点总数为2i+1
3、内部节点数为(n–1)/2
4、叶数为(n+1)/2
5、节点总数为2l–1
6、内部节点数为l–1
7、叶子的数量最多2^λ-1
class Node:
def __init__(self,item):
self.item=item
self.leftChild=None
self.rightChild=None
def isFullTree(root):
if root is None:
return True
if root.leftChild is None and root.rightChild is None:
return True
if root.leftChild is not None and root.rightChild is not None:
return(isFullTree(root.leftChild)and isFullTree(root.rightChild))
return False
root=Node(1)
root.rightChild=Node(3)
root.leftChild=Node(2)
root.leftChild.leftChild=Node(4)
root.leftChild.rightChild=Node(5)
root.leftChild.rightChild.leftChild=Node(6)
root.leftChild.rightChild.rightChild=Node(7)
if isFullTree(root):
print("The tree is a full binary tree")
else:
print("The tree is not a full binary tree")完美二叉树的每个内部节点都恰好有两个子节点,并且所有叶节点都在同一级别,如下图:
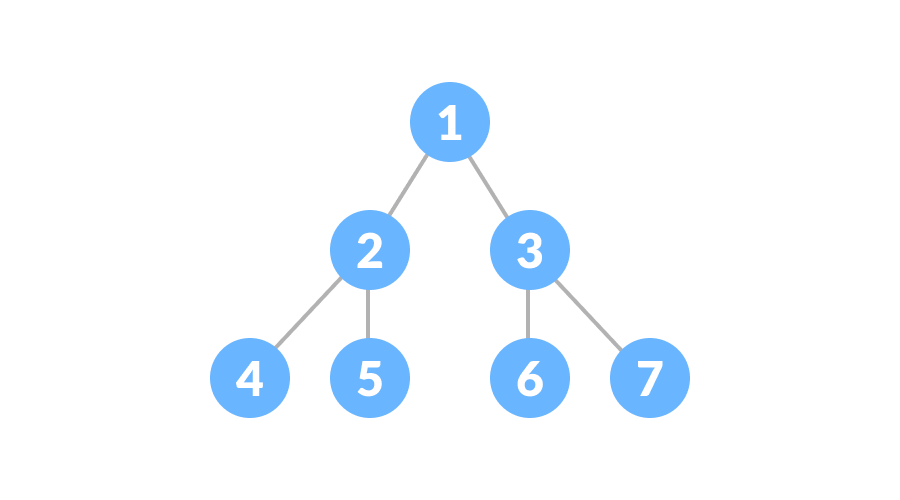
1、高度为h的完美二叉树有2^(h+1)–1个节点
2、具有n个节点的完美二叉树的高度为log(n+1)–1=Θ(ln(n))。
3、高度为h的完美二叉树具有2^h节点
4、完美二叉树中节点的平均深度为Θ(ln(n))。
class newNode:
def __init__(self,k):
self.key=k
self.right=self.left=None
def calculateDepth(node):
d=0
while(node is not None):
d+=1
node=node.left
return d
def is_perfect(root,d,level=0):
if(root is None):
return True
if(root.left is None and root.right is None):
return(d==level+1)
if(root.left is None or root.right is None):
return False
return(is_perfect(root.left,d,level+1)and
is_perfect(root.right,d,level+1))
root=None
root=newNode(1)
root.left=newNode(2)
root.right=newNode(3)
root.left.left=newNode(4)
root.left.right=newNode(5)
if(is_perfect(root,calculateDepth(root))):
print("The tree is a perfect binary tree")
else:
print("The tree is not a perfect binary tree")退化或病态树只具有左或右单个子节点的二叉树,如下图:
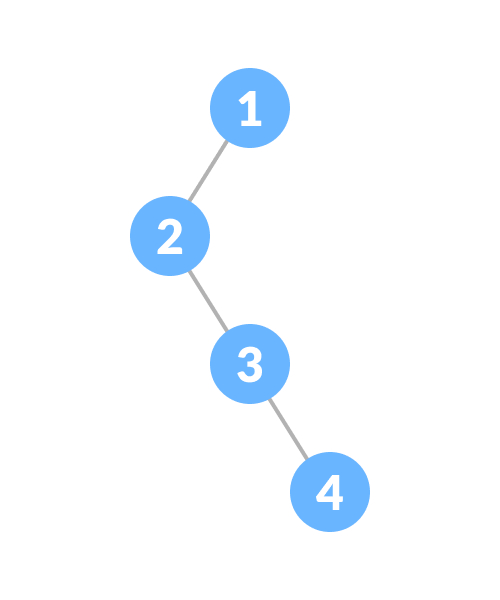
倾斜二叉树要么由左节点支配,要么由右节点支配。因此,有左二叉树和右二叉树两种类型,如下图:
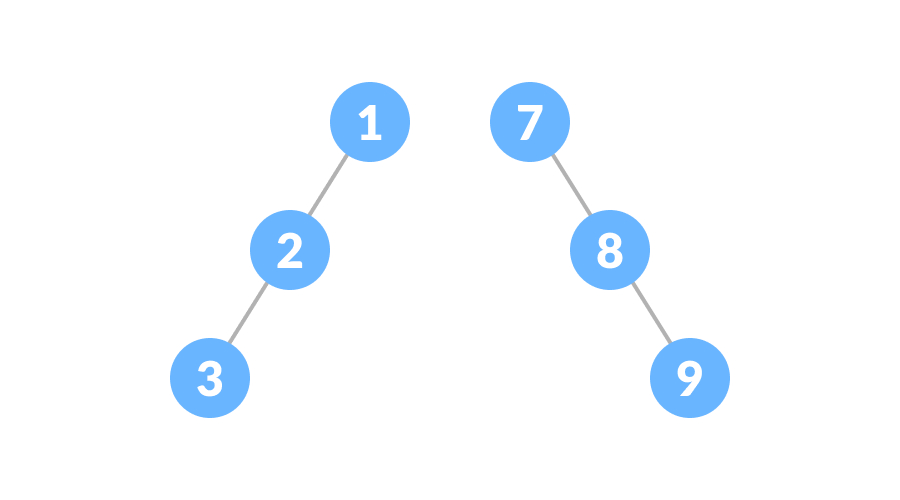
平衡二叉树每个节点的左子树和右子树的高度之差为0或1,如下图:
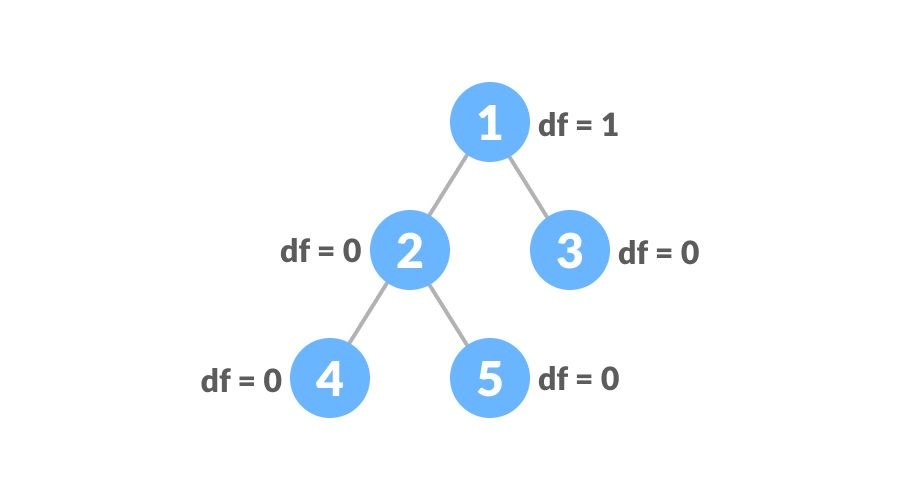
class Node: def __init__(self,data): self.data=data self.left=self.right=None class Height: def __init__(self): self.height=0 def isHeightBalanced(root,height): left_height=Height() right_height=Height() if root is None: return True l=isHeightBalanced(root.left,left_height) r=isHeightBalanced(root.right,right_height) height.height=max(left_height.height,right_height.height)+1 if abs(left_height.height-right_height.height)<=1: return l and r return False height=Height() root=Node(1) root.left=Node(2) root.right=Node(3) root.left.left=Node(4) root.left.right=Node(5) if isHeightBalanced(root,height): print('The tree is balanced') else: print('The tree is not balanced')
以上がPython を使用してさまざまな種類のバイナリ ツリーを判断する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。