
カーネル モデル ガウス プロセス (KMGP) は、さまざまなデータ セットの複雑さを処理するための高度なツールです。これは、カーネル関数を通じて従来のガウス プロセスの概念を拡張します。この記事では、KMGP の理論的基礎、実際の応用、課題について詳しく説明します。
カーネル モデルのガウス プロセスは、従来のガウス プロセスの拡張であり、機械学習と統計で使用されます。 kmgp を理解する前に、ガウス過程の基礎知識を習得し、カーネル モデルの役割を理解する必要があります。
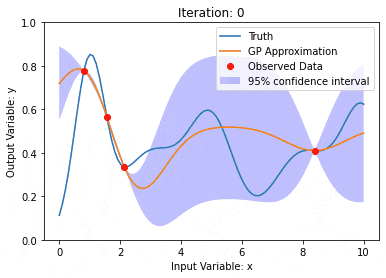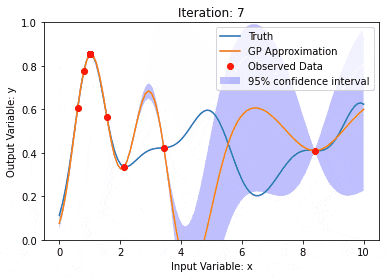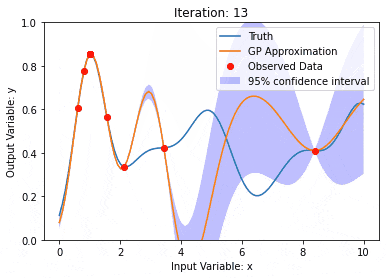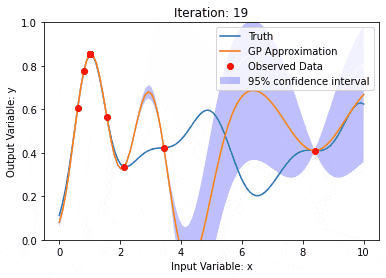
ガウス過程は一連の確率変数であり、有限数の変数はガウス分布と結合され、関数の確率分布を定義するために使用されます。
ガウス プロセスは、機械学習の回帰および分類タスクで一般的に使用され、データの確率分布を適合させるために使用できます。
ガウス プロセスの重要な特徴は、不確実性の推定と予測を提供できることです。これは、予測そのものと同じくらい重要である予測の信頼性を理解する作業に非常に役立ちます。
ガウス プロセスでは、カーネル関数 (または共分散関数) を使用して、異なるデータ ポイント間の差異を測定します。類似性。カーネル関数は 2 つの入力を受け取り、それらの間の類似性スコアを計算します。
カーネルには、線形、多項式、動径基底関数 (RBF) など、さまざまな種類があります。各コアには異なる特性があり、問題に応じて適切なコアを選択できます。
ガウス プロセスにおけるカーネル モデリングは、データ内の基礎となるパターンを最適に捕捉するためにカーネル関数を選択および最適化するプロセスです。カーネルの選択と構成がガウス プロセスのパフォーマンスに大きく影響する可能性があるため、この手順は非常に重要です。
KMGP は、カーネルのアプリケーションに焦点を当てた、標準 GP (ガウス プロセス) の拡張です。機能。標準 GP と比較して、KMGP は、特定の種類のデータまたは問題に基づいて、複雑なカーネル関数またはカスタム設計のカーネル関数をカスタマイズすることに重点を置いています。このアプローチは、データが複雑で、標準のカーネル関数が基礎となる関係を取得できない場合に特に役立ちます。ただし、KMGP でのカーネル機能の設計と調整は困難であり、多くの場合、問題領域と統計モデリングに関する深い領域知識と専門的経験が必要です。
カーネル モデルのガウス プロセスは、統計学習における洗練されたツールであり、複雑なデータ セットをモデル化する柔軟かつ強力な方法を提供します。特に、不確実性の推定値を提供する能力と、カスタム調整を通じてさまざまな種類のデータを調整する適応性が高く評価されています。
KMGP の適切に設計されたカーネルは、データ内の非線形傾向、周期性、不均一分散性 (さまざまなノイズ レベル) などの複雑な現象をモデル化できます。したがって、深いドメイン知識と統計モデリングの完全な理解が必要です。
KMGP はさまざまな分野に応用できます。地球統計学では、空間データをモデル化して、根底にある地理的変動を捉えます。金融では、株価を予測するために使用され、金融市場の不安定で複雑な性質を説明します。ロボット工学および制御システムでは、KMGP は不確実性の下での動的システムの動作をモデル化し、予測します。
合成データ セットを使用して、完全な Python コード サンプルを作成します。ここでは、特殊なライブラリ GPy を使用します。ガウス過程を扱うためのライブラリ。
pip install numpy matplotlib GPy
インポート ライブラリ
import numpy as np import matplotlib.pyplot as plt import GPy
次に、numpy を使用して合成データセットを作成します。
X = np.linspace(0, 10, 100)[:, None] Y = np.sin(X) + np.random.normal(0, 0.1, X.shape)
GPy を使用してガウス過程モデルを定義してトレーニングする
kernel = GPy.kern.RBF(input_dim=1, variance=1., lengthscale=1.) model = GPy.models.GPRegression(X, Y, kernel) model.optimize(messages=True)
モデルをトレーニングした後、それを使用してテストでの予測を行いますデータセット。次に、グラフをプロットしてモデルのパフォーマンスを視覚化します。
X_test = np.linspace(-2, 12, 200)[:, None] Y_pred, Y_var = model.predict(X_test) plt.figure(figsize=(10, 5)) plt.plot(X_test, Y_pred, 'r-', lw=2, label='Prediction') plt.fill_between(X_test.flatten(), (Y_pred - 2*np.sqrt(Y_var)).flatten(), (Y_pred + 2*np.sqrt(Y_var)).flatten(), alpha=0.5, color='pink', label='Confidence Interval') plt.scatter(X, Y, c='b', label='Training Data') plt.xlabel('X') plt.ylabel('Y') plt.title('Kernel Modeled Gaussian Process Regression') plt.legend() plt.show()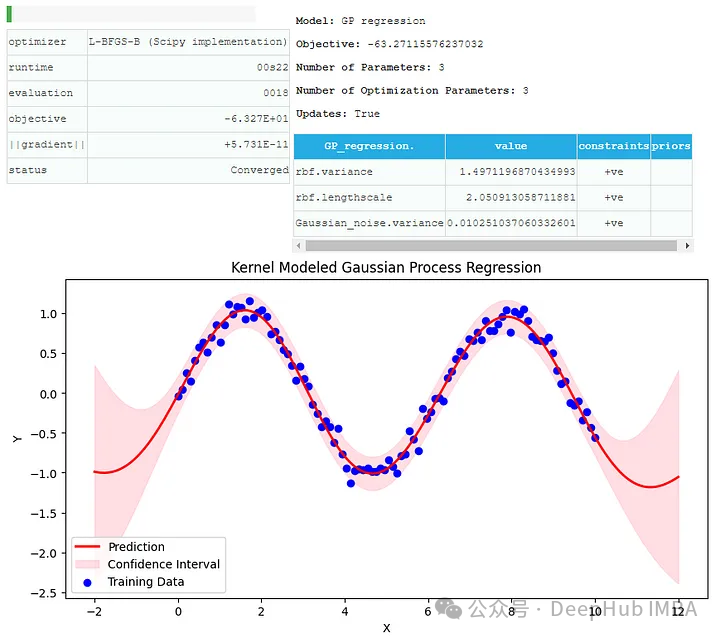
ここでは、RBF カーネルを使用してガウス過程回帰モデルを適用します。予測データとトレーニング データ、および信頼区間を確認できます。
カーネル モデルのガウス プロセスは、統計学習の分野における大きな進歩を表し、複雑なデータを理解するための柔軟で強力なフレームワークを提供します。データセット。 GPy には、基本的に私たちが確認できるすべてのカーネル関数も含まれています。以下は公式ドキュメントのスクリーンショットです:
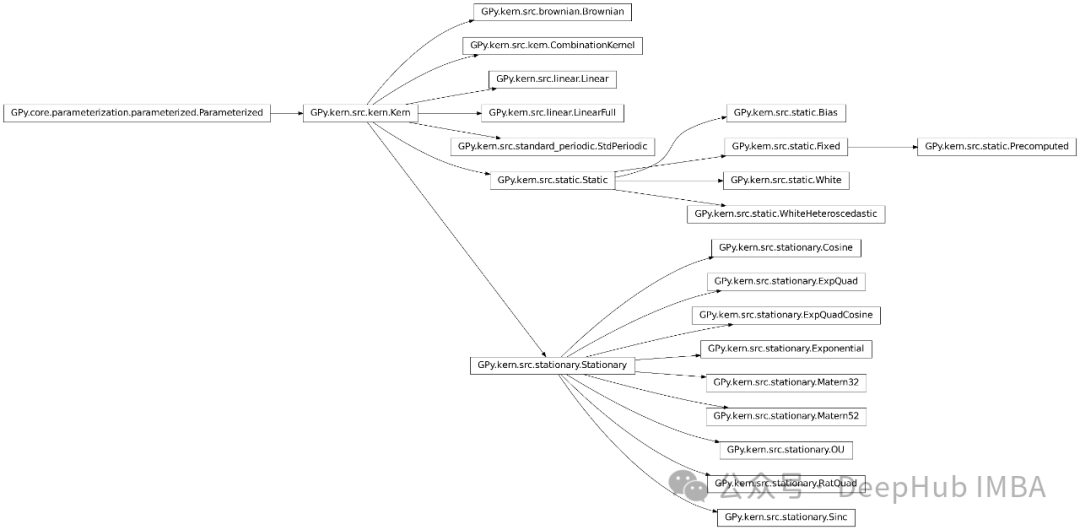
さまざまなデータについては、選択する必要がありますさまざまなカーネル関数カーネル ハイパーパラメータここで GPy 公式はフローチャートも提供します
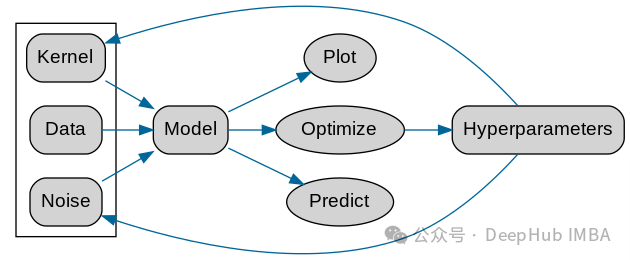
以上がカーネル モデル ガウス プロセス (KMGP) を使用したデータ モデリングの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。