スパース混合エキスパート アーキテクチャ言語モデル (MoE) をゼロから実装する方法を段階的に説明します。
この記事では、スパース混合エキスパート言語モデル (MoE) を実装する方法を紹介し、スパース混合エキスパートを使用して従来のフィードフォワードを置き換えるなど、モデルの実装プロセスを詳細に説明しますニューラル ネットワーク、Top-k ゲーティングとノイズを伴う Top-k ゲーティングを実現し、Kaiming He 初期化手法を使用します。著者らは、データセット処理、トークン化前処理、言語モデリング タスクなど、makemore アーキテクチャから変更されていない要素も示しています。最後に、モデルの実装プロセス全体について GitHub リポジトリへのリンクが提供されている、珍しい実践的な教科書です。
はじめに
混合エキスパート モデル (MoE) は、リリース後、特に疎混合エキスパート言語モデルで広く注目を集め始めました。ほとんどのコンポーネントは従来のトランスフォーマーに似ていますが、比較的単純に見えるにもかかわらず、スパース混合エキスパート言語モデルのトレーニングの安定性にいくつかの問題があります。
この構成可能な小規模スパース MoE 実装方法は、Hugging Face に関するブログで紹介されました。これは、新しい方法をすぐに試したい研究者にとって非常に役立つ可能性があります。このブログでは、PyTorch に基づく詳細なコードも提供しています。このコードは、https://github.com/AviSoori1x/makeMoE/tree/main にあります。このような小規模な実装は、研究者がこの分野で迅速な実験を行うのに役立ちます。
この Web サイトは、読者の利益のためにこれをまとめました。
この記事では、makemore アーキテクチャに基づいていくつかの変更を加えています:
-
個別のフィードフォワードの代わりに、まばらな混合エキスパートを使用しますニューラル ネットワーク;
Top-k ゲーティングとノイジーな Top-k ゲーティング;
パラメータの初期化には Kaiming He 初期化メソッドが使用されますが、この記事の重要な点はカスタマイズ可能です。初期化メソッド (Xavier/Glorot などの初期化メソッドの選択を含む)。
同時に、次のモジュールは makemore と一致しています:
データセット、前処理 (単語分割) 部分、および Andrej のオリジナルの選択言語モデリングのタスク - シェイクスピアのスタイルでテキスト コンテンツを生成する
カジュアルな自己注意メカニズム
トレーニング ループ
InferenceLogic
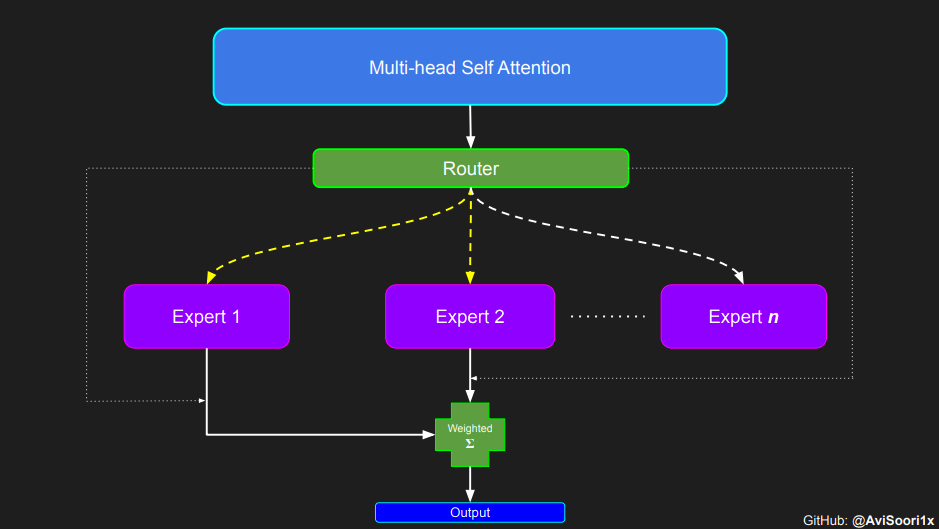
実装計画は、アテンション メカニズムから始めて段階的に紹介されます。
因果スケーリング ドット積アテンション メカニズム
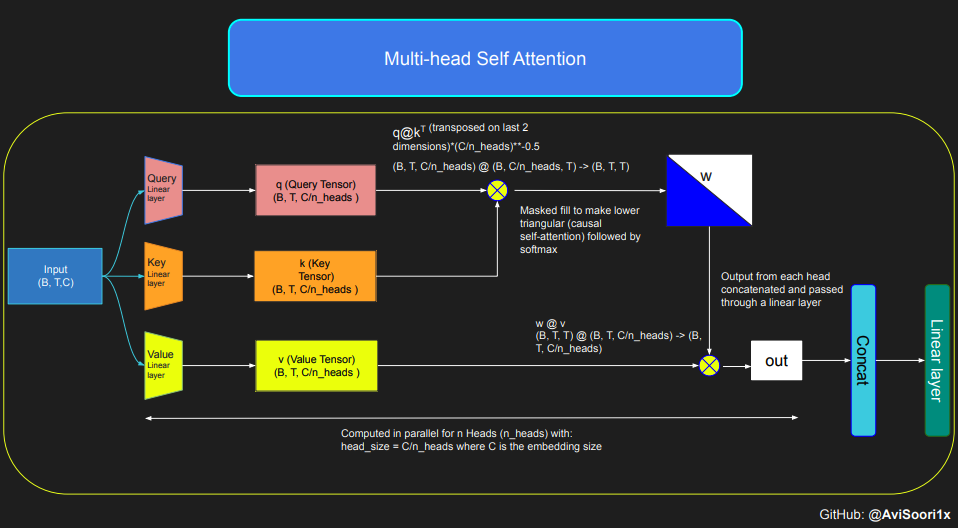
次のコードは、セルフ アテンション メカニズムの基本概念を示しており、以下に焦点を当てています。これは、古典的なスケーリングされたドット積自己注意を使用して実装されます。このセルフアテンションの変形では、クエリ行列、キー行列、および値行列はすべて同じ入力シーケンスから取得されます。同時に、特に純粋なデコーダ モデルにおいて、自己回帰言語生成プロセスの整合性を確保するために、マスキング メカニズムが使用されます。
このマスキング メカニズムは、現在のトークン位置以降の情報をマスクして、シーケンスの前の部分のみに焦点を当てるようにモデルを誘導できるため、非常に重要です。トークンの背後にあるコンテンツをブロックするこの種の注意は、因果的自己注意と呼ばれます。スパース混合エキスパート モデルは、デコーダのみの Transformer アーキテクチャに限定されないことに注意してください。実際、この分野における多くの重要な結果は T5 アーキテクチャを中心としており、これには Transformer モデルのエンコーダおよびデコーダ コンポーネントも含まれています。
#This code is borrowed from Andrej Karpathy's makemore repository linked in the repo.The self attention layers in Sparse mixture of experts models are the same asin regular transformer modelstorch.manual_seed(1337)B,T,C = 4,8,32 # batch, time, channelsx = torch.randn(B,T,C)# let's see a single Head perform self-attentionhead_size = 16key = nn.Linear(C, head_size, bias=False)query = nn.Linear(C, head_size, bias=False)value = nn.Linear(C, head_size, bias=False)k = key(x) # (B, T, 16)q = query(x) # (B, T, 16)wei =q @ k.transpose(-2, -1) # (B, T, 16) @ (B, 16, T) ---> (B, T, T)tril = torch.tril(torch.ones(T, T))#wei = torch.zeros((T,T))wei = wei.masked_fill(tril == 0, float('-inf'))wei = F.softmax(wei, dim=-1) #B,T,Tv = value(x) #B,T,Hout = wei @ v # (B,T,T) @ (B,T,H) -> (B,T,H)out.shape
torch.Size([4, 8, 16])
すると、因果的自己注意と多頭因果的自己注意のコードは次のように整理できます。マルチヘッド セルフ アテンションは複数のアテンション ヘッドを並行して適用し、各アテンション ヘッドはチャネルの一部 (埋め込み次元) のみに焦点を当てます。マルチヘッドセルフアテンションは本質的に学習プロセスを改善し、その固有の並列機能によりモデルトレーニングの効率を高めます。次のコードでは、ドロップアウトを使用して正則化を行い、過学習を防ぎます。
#Causal scaled dot product self-Attention Headn_embd = 64n_head = 4n_layer = 4head_size = 16dropout = 0.1class Head(nn.Module):""" one head of self-attention """def __init__(self, head_size):super().__init__()self.key = nn.Linear(n_embd, head_size, bias=False)self.query = nn.Linear(n_embd, head_size, bias=False)self.value = nn.Linear(n_embd, head_size, bias=False)self.register_buffer('tril', torch.tril(torch.ones(block_size, block_size)))self.dropout = nn.Dropout(dropout)def forward(self, x):B,T,C = x.shapek = self.key(x) # (B,T,C)q = self.query(x) # (B,T,C)# compute attention scores ("affinities")wei = q @ k.transpose(-2,-1) * C**-0.5 # (B, T, C) @ (B, C, T) -> (B, T, T)wei = wei.masked_fill(self.tril[:T, :T] == 0, float('-inf')) # (B, T, T)wei = F.softmax(wei, dim=-1) # (B, T, T)wei = self.dropout(wei)# perform the weighted aggregation of the valuesv = self.value(x) # (B,T,C)out = wei @ v # (B, T, T) @ (B, T, C) -> (B, T, C) return outマルチヘッドセルフアテンションの実装は次のとおりです:
#Multi-Headed Self Attentionclass MultiHeadAttention(nn.Module):""" multiple heads of self-attention in parallel """def __init__(self, num_heads, head_size):super().__init__()self.heads = nn.ModuleList([Head(head_size) for _ in range(num_heads)])self.proj = nn.Linear(n_embd, n_embd)self.dropout = nn.Dropout(dropout)def forward(self, x):out = torch.cat([h(x) for h in self.heads], dim=-1)out = self.dropout(self.proj(out)) return out
エキスパート モジュールを作成します
つまり、単純な多層パーセプトロンです。
スパース混合エキスパート アーキテクチャでは、各変換ブロック内のセルフアテンション メカニズムは変更されません。ただし、各ブロックの構造は劇的に変化します。標準のフィードフォワード ニューラル ネットワークは、まばらに活性化される複数のフィードフォワード ネットワーク (つまり、エキスパート ネットワーク) に置き換えられます。いわゆる「スパースアクティベーション」とは、シーケンス内の各トークンが限られた数の専門家 (通常は 1 人または 2 人) にのみ割り当てられることを意味します。 这有助于提高训练和推理速度,因为每次前向传递都会激活少数专家。不过,所有专家都必须存在 GPU 内存中,因此当参数总数达到数千亿甚至数万亿时,就会产生部署方面的问题。 Top-k 门控的一个例子 门控网络,也称为路由,确定哪个专家网络接收来自多头注意力的 token 的输出。举个例子解释路由的机制,假设有 4 个专家,token 需要被路由到前 2 个专家中。首先需要通过线性层将 token 输入到门控网络中。该层将对应于(Batch size,Tokens,n_embed)的输入张量从(2,4,32)维度,投影到对应于(Batch size、Tokens,num_expert)的新形状:(2、4,4)。其中 n_embed 是输入的通道维度,num_experts 是专家网络的计数。 接下来,沿最后一个维度,找出最大的前两个值及其相应的索引。 通过仅保留沿最后一个维度进行比较的前 k 大的值,来获得稀疏门控的输出。用负无穷值填充其余部分,在使用 softmax 激活函数。负无穷会被映射至零,而最大的前两个值会更加突出,且和为 1。要求和为 1 是为了对专家输出的内容进行加权。 使用有噪声的 top-k 门控以实现负载平衡 接下来使用下面这段代码来测试程序: 尽管最近发布的 mixtral 的论文没有提到这一点,但本文的作者相信有噪声的 Top-k 门控机制是训练 MoE 模型的一个重要工具。从本质上讲,不会希望所有的 token 都发送给同一组「受欢迎」的专家网络。人们需要的是能在开发和探索之间取得良好平衡。为此,为了负载平衡,从门控的线性层向 logits 激活函数添加标准正态噪声是有帮助的,这使训练更有效率。 再次尝试代码: 创建稀疏化的混合专家模块 在获得门控网络的输出结果之后,对于给定的 token,将前 k 个值选择性地与来自相应的前 k 个专家的输出相乘。这种选择性乘法的结果是一个加权和,该加权和构成 SparseMoe 模块的输出。这个过程的关键和难点是避免不必要的乘法运算,只为前 k 名专家进行正向转播。为每个专家执行前向传播将破坏使用稀疏 MoE 的目的,因为这个过程将不再是稀疏的。 运行以下代码来用样本测试上述实现,可以看到确实如此! 需要强调的是,如上代码所示,从路由 / 门控网络输出的 top_k 本身也很重要。索引确定了被激活的专家是哪些, 对应的值又决定了权重大小。下图进一步解释了加权求和的概念。 模块整合 将多头自注意力和稀疏混合专家相结合,形成稀疏混合专家 transformer 块。就像在 vanilla transformer 块中一样,也要使用残差以确保训练稳定,并避免梯度消失等问题。此外,要采用层归一化来进一步稳定学习过程。 最后,将所有内容整合在一起,形成稀疏混合专家语言模型。 参数初始化对于深度神经网络的高效训练非常重要。由于专家中存在 ReLU 激活,因此这里使用了 Kaiming He 初始化。也可以尝试在 transformer 中更常用的 Glorot 初始化。杰里米 - 霍华德(Jeremy Howard)的《Fastai》第 2 部分有一个从头开始实现这些功能的精彩讲座:https://course.fast.ai/Lessons/lesson17.html Glorot 参数初始化通常被用于 transformer 模型,因此这是一个可能提高模型性能的方法。 本文作者使用 mlflow 跟踪并记录重要指标和训练超参数。 记录训练和验证损失可以很好地指示训练的进展情况。该图显示,可能应该在 4500 次时停止(当验证损失稍微增加时) 接下来可以使用这个模型逐字符自回归地生成文本。 本文参考内容: 在实施过程中,作者大量参考了以下出版物: 混合专家模型:https://arxiv.org/pdf/2401.04088.pdf 超大型神经网络:稀疏门控混合专家层:https://arxiv.org/pdf/1701.06538.pdf 来自 Andrej Karpathy 的原始 makemore 实现:https://github.com/karpathy/makemore 还可以尝试以下几种方法,来提高模型性能: 提高混合专家模块的效率; 尝试不同的神经网络初始化策略; 从字符级到子词级的分词; 对专家数量和 k 的取值(每个 token 激活的专家数量)进行贝叶斯超参数搜索。这可以归类为神经架构搜索。 优化专家能力。 以上がスパース混合エキスパート アーキテクチャ言語モデル (MoE) をゼロから実装する方法を段階的に説明します。の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。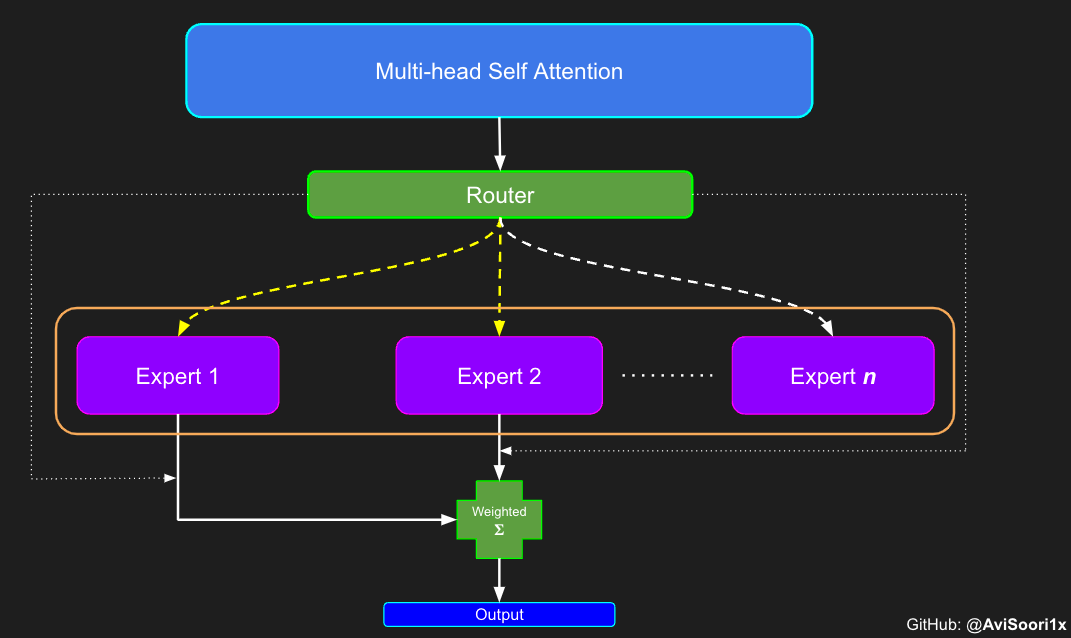
#Expert moduleclass Expert(nn.Module):""" An MLP is a simple linear layer followed by a non-linearity i.e. each Expert """def __init__(self, n_embd):super().__init__()self.net = nn.Sequential(nn.Linear(n_embd, 4 * n_embd),nn.ReLU(),nn.Linear(4 * n_embd, n_embd),nn.Dropout(dropout),)def forward(self, x): return self.net(x)
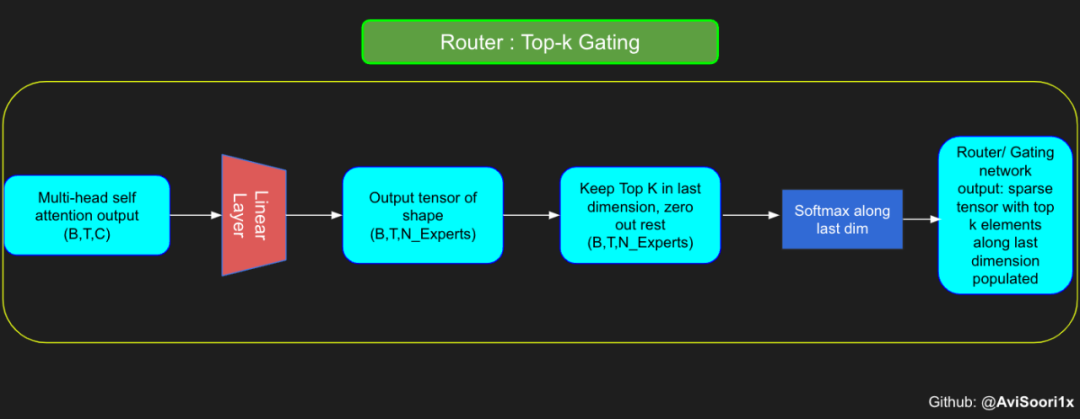
#Understanding how gating worksnum_experts = 4top_k=2n_embed=32#Example multi-head attention output for a simple illustrative example, consider n_embed=32, context_length=4 and batch_size=2mh_output = torch.randn(2, 4, n_embed)topkgate_linear = nn.Linear(n_embed, num_experts) # nn.Linear(32, 4)logits = topkgate_linear(mh_output)top_k_logits, top_k_indices = logits.topk(top_k, dim=-1)# Get top-k expertstop_k_logits, top_k_indices
#output:(tensor([[[ 0.0246, -0.0190],[ 0.1991,0.1513],[ 0.9749,0.7185],[ 0.4406, -0.8357]], [[ 0.6206, -0.0503],[ 0.8635,0.3784],[ 0.6828,0.5972],[ 0.4743,0.3420]]], grad_fn=<TopkBackward0>), tensor([[[2, 3],[2, 1],[3, 1],[2, 1]], [[0, 2], [0, 3], [3, 2], [3, 0]]]))
zeros = torch.full_like(logits, float('-inf')) #full_like clones a tensor and fills it with a specified value (like infinity) for masking or calculations.sparse_logits = zeros.scatter(-1, top_k_indices, top_k_logits)sparse_logits
#outputtensor([[[ -inf,-inf,0.0246, -0.0190], [ -inf,0.1513,0.1991,-inf], [ -inf,0.7185,-inf,0.9749], [ -inf, -0.8357,0.4406,-inf]],[[ 0.6206,-inf, -0.0503,-inf], [ 0.8635,-inf,-inf,0.3784], [ -inf,-inf,0.5972,0.6828], [ 0.3420,-inf,-inf,0.4743]]], grad_fn=<ScatterBackward0>)
gating_output= F.softmax(sparse_logits, dim=-1)gating_output
#ouputtensor([[[0.0000, 0.0000, 0.5109, 0.4891], [0.0000, 0.4881, 0.5119, 0.0000], [0.0000, 0.4362, 0.0000, 0.5638], [0.0000, 0.2182, 0.7818, 0.0000]],[[0.6617, 0.0000, 0.3383, 0.0000], [0.6190, 0.0000, 0.0000, 0.3810], [0.0000, 0.0000, 0.4786, 0.5214], [0.4670, 0.0000, 0.0000, 0.5330]]], grad_fn=<SoftmaxBackward0>)
# First define the top k router moduleclass TopkRouter(nn.Module):def __init__(self, n_embed, num_experts, top_k):super(TopkRouter, self).__init__()self.top_k = top_kself.linear =nn.Linear(n_embed, num_experts) def forward(self, mh_ouput):# mh_ouput is the output tensor from multihead self attention blocklogits = self.linear(mh_output)top_k_logits, indices = logits.topk(self.top_k, dim=-1)zeros = torch.full_like(logits, float('-inf'))sparse_logits = zeros.scatter(-1, indices, top_k_logits)router_output = F.softmax(sparse_logits, dim=-1) return router_output, indices
#Testing this out:num_experts = 4top_k = 2n_embd = 32mh_output = torch.randn(2, 4, n_embd)# Example inputtop_k_gate = TopkRouter(n_embd, num_experts, top_k)gating_output, indices = top_k_gate(mh_output)gating_output.shape, gating_output, indices#And it works!!
#output(torch.Size([2, 4, 4]), tensor([[[0.5284, 0.0000, 0.4716, 0.0000],[0.0000, 0.4592, 0.0000, 0.5408],[0.0000, 0.3529, 0.0000, 0.6471],[0.3948, 0.0000, 0.0000, 0.6052]], [[0.0000, 0.5950, 0.4050, 0.0000], [0.4456, 0.0000, 0.5544, 0.0000], [0.7208, 0.0000, 0.0000, 0.2792], [0.0000, 0.0000, 0.5659, 0.4341]]], grad_fn=<SoftmaxBackward0>), tensor([[[0, 2],[3, 1],[3, 1],[3, 0]], [[1, 2], [2, 0], [0, 3], [2, 3]]]))
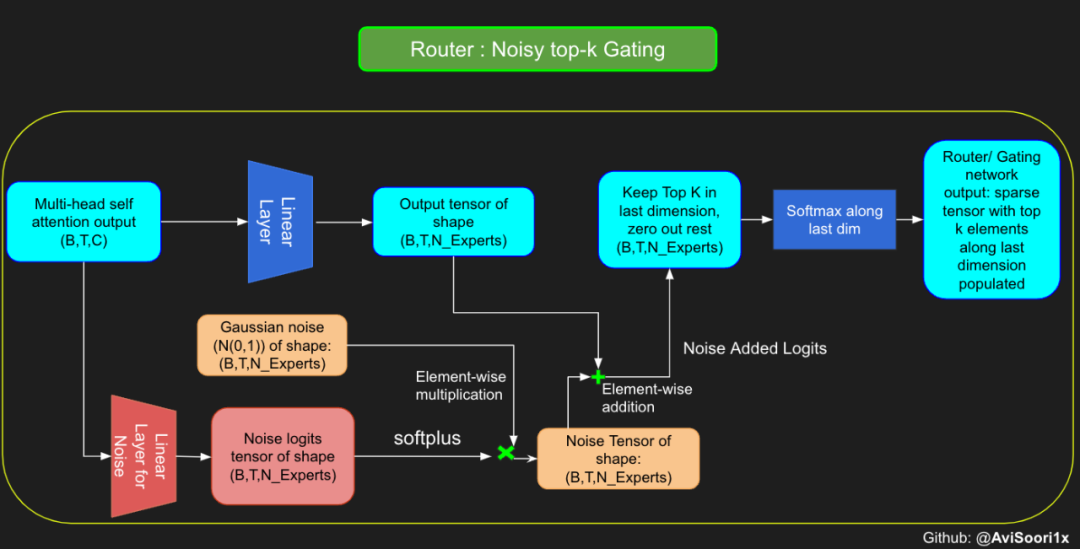
#Changing the above to accomodate noisy top-k gatingclass NoisyTopkRouter(nn.Module):def __init__(self, n_embed, num_experts, top_k):super(NoisyTopkRouter, self).__init__()self.top_k = top_k#layer for router logitsself.topkroute_linear = nn.Linear(n_embed, num_experts)self.noise_linear =nn.Linear(n_embed, num_experts)def forward(self, mh_output):# mh_ouput is the output tensor from multihead self attention blocklogits = self.topkroute_linear(mh_output)#Noise logitsnoise_logits = self.noise_linear(mh_output)#Adding scaled unit gaussian noise to the logitsnoise = torch.randn_like(logits)*F.softplus(noise_logits)noisy_logits = logits + noisetop_k_logits, indices = noisy_logits.topk(self.top_k, dim=-1)zeros = torch.full_like(noisy_logits, float('-inf'))sparse_logits = zeros.scatter(-1, indices, top_k_logits)router_output = F.softmax(sparse_logits, dim=-1) return router_output, indices
#Testing this out, again:num_experts = 8top_k = 2n_embd = 16mh_output = torch.randn(2, 4, n_embd)# Example inputnoisy_top_k_gate = NoisyTopkRouter(n_embd, num_experts, top_k)gating_output, indices = noisy_top_k_gate(mh_output)gating_output.shape, gating_output, indices#It works!!
#output(torch.Size([2, 4, 8]), tensor([[[0.4181, 0.0000, 0.5819, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],[0.4693, 0.5307, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],[0.0000, 0.4985, 0.5015, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],[0.0000, 0.0000, 0.0000, 0.2641, 0.0000, 0.7359, 0.0000, 0.0000]], [[0.0000, 0.0000, 0.0000, 0.6301, 0.0000, 0.3699, 0.0000, 0.0000], [0.0000, 0.0000, 0.0000, 0.4766, 0.0000, 0.0000, 0.0000, 0.5234], [0.0000, 0.0000, 0.0000, 0.6815, 0.0000, 0.0000, 0.3185, 0.0000], [0.4482, 0.5518, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000]]], grad_fn=<SoftmaxBackward0>), tensor([[[2, 0],[1, 0],[2, 1],[5, 3]], [[3, 5], [7, 3], [3, 6], [1, 0]]]))
class SparseMoE(nn.Module):def __init__(self, n_embed, num_experts, top_k):super(SparseMoE, self).__init__()self.router = NoisyTopkRouter(n_embed, num_experts, top_k)self.experts = nn.ModuleList([Expert(n_embed) for _ in range(num_experts)])self.top_k = top_kdef forward(self, x):gating_output, indices = self.router(x)final_output = torch.zeros_like(x)# Reshape inputs for batch processingflat_x = x.view(-1, x.size(-1))flat_gating_output = gating_output.view(-1, gating_output.size(-1))# Process each expert in parallelfor i, expert in enumerate(self.experts):# Create a mask for the inputs where the current expert is in top-kexpert_mask = (indices == i).any(dim=-1)flat_mask = expert_mask.view(-1)if flat_mask.any():expert_input = flat_x[flat_mask]expert_output = expert(expert_input)# Extract and apply gating scoresgating_scores = flat_gating_output[flat_mask, i].unsqueeze(1)weighted_output = expert_output * gating_scores# Update final output additively by indexing and addingfinal_output[expert_mask] += weighted_output.squeeze(1) return final_output
import torchimport torch.nn as nn#Let's test this outnum_experts = 8top_k = 2n_embd = 16dropout=0.1mh_output = torch.randn(4, 8, n_embd)# Example multi-head attention outputsparse_moe = SparseMoE(n_embd, num_experts, top_k)final_output = sparse_moe(mh_output)print("Shape of the final output:", final_output.shape)Shape of the final output: torch.Size([4, 8, 16])
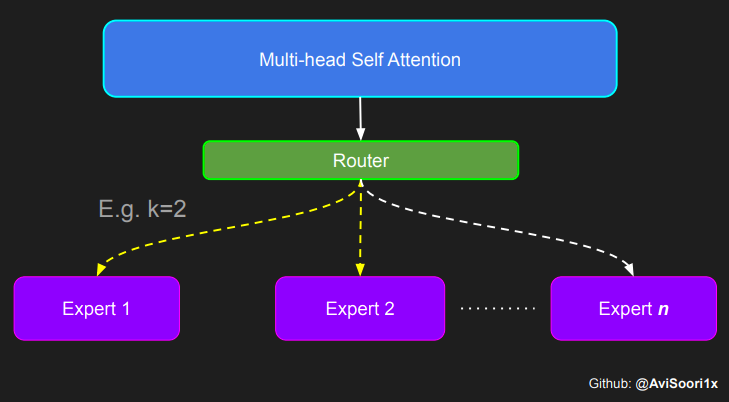
#Create a self attention + mixture of experts block, that may be repeated several number of timesclass Block(nn.Module):""" Mixture of Experts Transformer block: communication followed by computation (multi-head self attention + SparseMoE) """def __init__(self, n_embed, n_head, num_experts, top_k):# n_embed: embedding dimension, n_head: the number of heads we'd likesuper().__init__()head_size = n_embed // n_headself.sa = MultiHeadAttention(n_head, head_size)self.smoe = SparseMoE(n_embed, num_experts, top_k)self.ln1 = nn.LayerNorm(n_embed)self.ln2 = nn.LayerNorm(n_embed)def forward(self, x):x = x + self.sa(self.ln1(x))x = x + self.smoe(self.ln2(x)) return x
class SparseMoELanguageModel(nn.Module):def __init__(self):super().__init__()# each token directly reads off the logits for the next token from a lookup table self.token_embedding_table = nn.Embedding(vocab_size, n_embed) self.position_embedding_table = nn.Embedding(block_size, n_embed)self.blocks = nn.Sequential(*[Block(n_embed, n_head=n_head, num_experts=num_experts,top_k=top_k) for _ in range(n_layer)])self.ln_f = nn.LayerNorm(n_embed) # final layer normself.lm_head = nn.Linear(n_embed, vocab_size)def forward(self, idx, targets=None):B, T = idx.shape# idx and targets are both (B,T) tensor of integerstok_emb = self.token_embedding_table(idx) # (B,T,C)pos_emb = self.position_embedding_table(torch.arange(T, device=device)) # (T,C)x = tok_emb + pos_emb # (B,T,C)x = self.blocks(x) # (B,T,C)x = self.ln_f(x) # (B,T,C)logits = self.lm_head(x) # (B,T,vocab_size)if targets is None:loss = Noneelse:B, T, C = logits.shapelogits = logits.view(B*T, C)targets = targets.view(B*T)loss = F.cross_entropy(logits, targets)return logits, lossdef generate(self, idx, max_new_tokens):# idx is (B, T) array of indices in the current contextfor _ in range(max_new_tokens):# crop idx to the last block_size tokensidx_cond = idx[:, -block_size:]# get the predictionslogits, loss = self(idx_cond)# focus only on the last time steplogits = logits[:, -1, :] # becomes (B, C)# apply softmax to get probabilitiesprobs = F.softmax(logits, dim=-1) # (B, C)# sample from the distributionidx_next = torch.multinomial(probs, num_samples=1) # (B, 1)# append sampled index to the running sequenceidx = torch.cat((idx, idx_next), dim=1) # (B, T+1) return idx
def kaiming_init_weights(m):if isinstance (m, (nn.Linear)): init.kaiming_normal_(m.weight)model = SparseMoELanguageModel()model.apply(kaiming_init_weights)
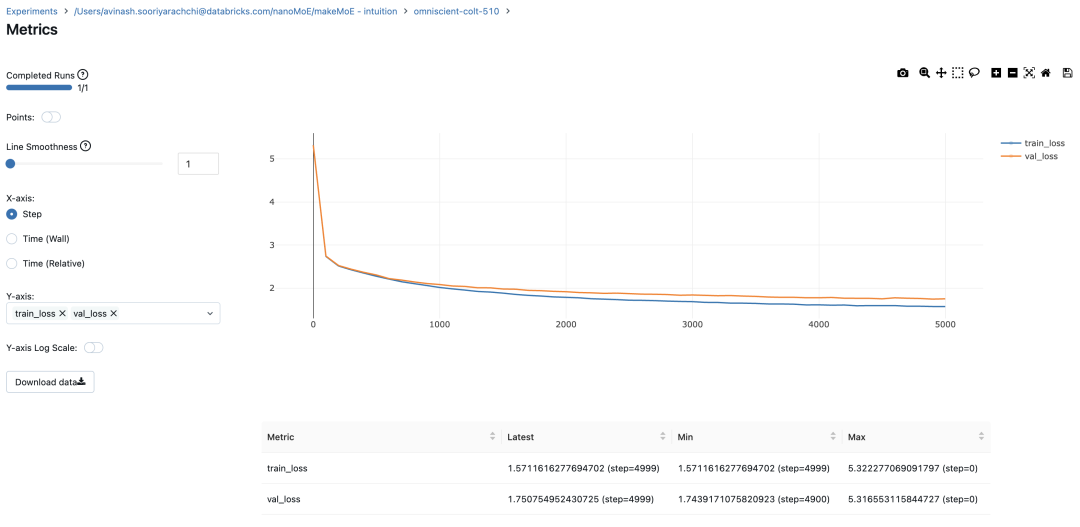
#Using MLFlowm = model.to(device)# print the number of parameters in the modelprint(sum(p.numel() for p in m.parameters())/1e6, 'M parameters')# create a PyTorch optimizeroptimizer = torch.optim.AdamW(model.parameters(), lr=learning_rate)#mlflow.set_experiment("makeMoE")with mlflow.start_run():#If you use mlflow.autolog() this will be automatically logged. I chose to explicitly log here for completenessparams = {"batch_size": batch_size , "block_size" : block_size, "max_iters": max_iters, "eval_interval": eval_interval,"learning_rate": learning_rate, "device": device, "eval_iters": eval_iters, "dropout" : dropout, "num_experts": num_experts, "top_k": top_k }mlflow.log_params(params)for iter in range(max_iters):# every once in a while evaluate the loss on train and val setsif iter % eval_interval == 0 or iter == max_iters - 1:losses = estimate_loss()print(f"step {iter}: train loss {losses['train']:.4f}, val loss {losses['val']:.4f}")metrics = {"train_loss": losses['train'], "val_loss": losses['val']}mlflow.log_metrics(metrics, step=iter)# sample a batch of dataxb, yb = get_batch('train')# evaluate the losslogits, loss = model(xb, yb)optimizer.zero_grad(set_to_none=True)loss.backward()optimizer.step()8.996545 M parametersstep 0: train loss 5.3223, val loss 5.3166step 100: train loss 2.7351, val loss 2.7429step 200: train loss 2.5125, val loss 2.5233...step 4999: train loss 1.5712, val loss 1.7508
# generate from the model. Not great. Not too bad eithercontext = torch.zeros((1, 1), dtype=torch.long, device=device)print(decode(m.generate(context, max_new_tokens=2000)[0].tolist()))
DUKE VINCENVENTIO:If it ever fecond he town sue kigh now,That thou wold'st is steen 't.SIMNA:Angent her; no, my a born Yorthort,Romeoos soun and lawf to your sawe with ch a woft ttastly defy,To declay the soul art; and meart smad.CORPIOLLANUS:Which I cannot shall do from by born und ot cold warrike,What king we best anone wrave's going of heard and goodThus playvage; you have wold the grace....

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7695
7695
 15
15
 1640
1640
 14
14
 1393
1393
 52
52
 1287
1287
 25
25
 1229
1229
 29
29
 パデュー大学による、時間をかける価値のある拡散モデルのチュートリアル
Apr 07, 2024 am 09:01 AM
パデュー大学による、時間をかける価値のある拡散モデルのチュートリアル
Apr 07, 2024 am 09:01 AM
拡散はより良いものを模倣するだけでなく、「創造」することもできます。拡散モデル(DiffusionModel)は、画像生成モデルである。 AI 分野でよく知られている GAN や VAE などのアルゴリズムと比較すると、拡散モデルは異なるアプローチを採用しており、その主な考え方は、最初に画像にノイズを追加し、その後徐々にノイズを除去するプロセスです。ノイズを除去して元の画像を復元する方法は、アルゴリズムの中核部分です。最後のアルゴリズムは、ランダムなノイズを含む画像から画像を生成できます。近年、生成 AI の驚異的な成長により、テキストから画像への生成、ビデオ生成など、多くのエキサイティングなアプリケーションが可能になりました。これらの生成ツールの背後にある基本原理は、以前の方法の制限を克服する特別なサンプリング メカニズムである拡散の概念です。
 ワンクリックでPPTを生成!キミ: まずは「PPT出稼ぎ労働者」を普及させましょう
Aug 01, 2024 pm 03:28 PM
ワンクリックでPPTを生成!キミ: まずは「PPT出稼ぎ労働者」を普及させましょう
Aug 01, 2024 pm 03:28 PM
キミ: たった 1 文の PPT がわずか 10 秒で完成します。 PPTはとても面倒です!会議を開催するには PPT が必要であり、週次報告書を作成するには PPT が必要であり、投資を勧誘するには PPT を提示する必要があり、不正行為を告発するには PPT を送信する必要があります。大学は、PPT 専攻を勉強するようなものです。授業中に PPT を見て、授業後に PPT を行います。おそらく、デニス オースティンが 37 年前に PPT を発明したとき、PPT がこれほど普及する日が来るとは予想していなかったでしょう。 PPT 作成の大変な経験を話すと涙が出ます。 「20 ページを超える PPT を作成するのに 3 か月かかり、何十回も修正しました。PPT を見ると吐きそうになりました。」 「ピーク時には 1 日に 5 枚の PPT を作成し、息をすることさえありました。」 PPTでした。」 即席の会議をするなら、そうすべきです
 CVPR 2024 のすべての賞が発表されました!オフラインでのカンファレンスには1万人近くが参加し、Googleの中国人研究者が最優秀論文賞を受賞した
Jun 20, 2024 pm 05:43 PM
CVPR 2024 のすべての賞が発表されました!オフラインでのカンファレンスには1万人近くが参加し、Googleの中国人研究者が最優秀論文賞を受賞した
Jun 20, 2024 pm 05:43 PM
北京時間6月20日早朝、シアトルで開催されている最高の国際コンピュータビジョンカンファレンス「CVPR2024」が、最優秀論文やその他の賞を正式に発表した。今年は、最優秀論文 2 件と学生優秀論文 2 件を含む合計 10 件の論文が賞を受賞しました。また、最優秀論文ノミネートも 2 件、学生優秀論文ノミネートも 4 件ありました。コンピュータービジョン (CV) 分野のトップカンファレンスは CVPR で、毎年多数の研究機関や大学が集まります。統計によると、今年は合計 11,532 件の論文が投稿され、2,719 件が採択され、採択率は 23.6% でした。ジョージア工科大学による CVPR2024 データの統計分析によると、研究テーマの観点から最も論文数が多いのは画像とビデオの合成と生成です (Imageandvideosyn
 ベアメタルから 700 億のパラメータを備えた大規模モデルまで、チュートリアルとすぐに使えるスクリプトがここにあります
Jul 24, 2024 pm 08:13 PM
ベアメタルから 700 億のパラメータを備えた大規模モデルまで、チュートリアルとすぐに使えるスクリプトがここにあります
Jul 24, 2024 pm 08:13 PM
LLM が大量のデータを使用して大規模なコンピューター クラスターでトレーニングされていることはわかっています。このサイトでは、LLM トレーニング プロセスを支援および改善するために使用される多くの方法とテクノロジが紹介されています。今日、私たちが共有したいのは、基礎となるテクノロジーを深く掘り下げ、オペレーティング システムさえ持たない大量の「ベア メタル」を LLM のトレーニング用のコンピューター クラスターに変える方法を紹介する記事です。この記事は、機械がどのように考えるかを理解することで一般的な知能の実現に努めている AI スタートアップ企業 Imbue によるものです。もちろん、オペレーティング システムを持たない大量の「ベア メタル」を LLM をトレーニングするためのコンピューター クラスターに変換することは、探索と試行錯誤に満ちた簡単なプロセスではありませんが、Imbue は最終的に 700 億のパラメータを備えた LLM のトレーニングに成功しました。プロセスが蓄積する
 PyCharm Community Edition インストール ガイド: すべての手順をすばやくマスターする
Jan 27, 2024 am 09:10 AM
PyCharm Community Edition インストール ガイド: すべての手順をすばやくマスターする
Jan 27, 2024 am 09:10 AM
PyCharm コミュニティ版のクイック スタート: 詳細なインストール チュートリアル 完全な分析 はじめに: PyCharm は、開発者が Python コードをより効率的に作成できるようにする包括的なツール セットを提供する強力な Python 統合開発環境 (IDE) です。この記事では、PyCharm Community Edition のインストール方法を詳しく紹介し、初心者がすぐに使い始めるのに役立つ具体的なコード例を示します。ステップ 1: PyCharm Community Edition をダウンロードしてインストールする PyCharm を使用するには、まず公式 Web サイトからダウンロードする必要があります
 AIの活用 | AIが一人暮らしの女の子の生活ビデオブログを作成、3日間で数万件の「いいね!」を獲得
Aug 07, 2024 pm 10:53 PM
AIの活用 | AIが一人暮らしの女の子の生活ビデオブログを作成、3日間で数万件の「いいね!」を獲得
Aug 07, 2024 pm 10:53 PM
Machine Power Report 編集者: Yang Wen 大型モデルや AIGC に代表される人工知能の波は、私たちの生活や働き方を静かに変えていますが、ほとんどの人はまだその使い方を知りません。そこで、直感的で興味深く、簡潔な人工知能のユースケースを通じてAIの活用方法を詳しく紹介し、皆様の思考を刺激するコラム「AI in Use」を立ち上げました。また、読者が革新的な実践的な使用例を提出することも歓迎します。ビデオリンク: https://mp.weixin.qq.com/s/2hX_i7li3RqdE4u016yGhQ 最近、Xiaohongshu で一人暮らしの女の子の生活 vlog が人気になりました。イラスト風のアニメーションといくつかの癒しの言葉を組み合わせれば、数日で簡単に習得できます。
 C言語学習を始めるためのプログラミングソフト5選
Feb 19, 2024 pm 04:51 PM
C言語学習を始めるためのプログラミングソフト5選
Feb 19, 2024 pm 04:51 PM
C言語は広く使われているプログラミング言語であり、コンピュータプログラミングを志す人にとって必ず学ばなければならない基本的な言語の一つです。ただし、初心者にとって、特に関連する学習ツールや教材が不足しているため、新しいプログラミング言語を学習するのは難しい場合があります。この記事では、C言語初心者がすぐに始められるプログラミングソフトを5つ紹介します。最初のプログラミング ソフトウェアは Code::Blocks でした。 Code::Blocks は、無料のオープンソース統合開発環境 (IDE) です。
 技術初心者必読:C言語とPythonの難易度分析
Mar 22, 2024 am 10:21 AM
技術初心者必読:C言語とPythonの難易度分析
Mar 22, 2024 am 10:21 AM
タイトル: 技術初心者必読: 具体的なコード例を必要とする C 言語と Python の難易度分析 今日のデジタル時代において、プログラミング技術はますます重要な能力となっています。ソフトウェア開発、データ分析、人工知能などの分野で働きたい場合でも、単に興味があってプログラミングを学びたい場合でも、適切なプログラミング言語を選択することが最初のステップです。数あるプログラミング言語の中でも、C言語とPythonは広く使われているプログラミング言語であり、それぞれに独自の特徴があります。この記事ではC言語とPythonの難易度を分析します。




