拡散モデルは、画像生成における優れたパフォーマンスにより、生成モデルの新時代を切り開きます。 Stable Diffusion、DALLE、Imagen、SORA などの大規模なモデルが登場し、生成 AI の応用の可能性がさらに豊かになりました。しかし、現在の拡散モデルは理論的には完璧ではなく、サンプリング時間のエンドポイントにおける未定義の特異点の問題に注目した研究はほとんどありません。さらに、アプリケーションの特異点問題によって引き起こされる平均グレーレベルや、生成される画像の品質に影響を与えるその他の問題は解決されていません。 この問題を解決するために、WeChat ビジョン チームは中山大学と協力して拡散モデルの特異点問題を共同で調査し、プラグアンド アンド ソリューションを提案しました。 play メソッドを使用して、初期段階でのサンプリング問題を効果的に解決します。この方法は、平均グレーレベルの問題を解決し、既存の拡散モデルの生成能力を大幅に向上させます。研究結果はCVPR 2024カンファレンスで発表された。 拡散モデルは、画像、音声、テキスト、ビデオの生成など、マルチモーダルなコンテンツ生成タスクで目覚ましい成功を収めています。これらのモデルのモデリングが成功するかどうかは、主に、 拡散プロセスの逆プロセスもガウス特性 に準拠するという仮定に依存しています。ただし、この仮説は完全には証明されていません。特にエンドポイント、つまり t=0 または t=1 では特異点の問題が発生し、特異点でのサンプリングを研究する既存の方法が制限されます。 さらに、特異点問題は拡散モデルの生成能力にも影響し、モデルに 平均グレースケール問題 が発生します。 , 以下に示すように、明るさの強い画像や弱い画像を生成することは困難です。これにより、現在の普及モデルの適用範囲もある程度制限されます。 時間エンドポイントにおける拡散モデルの特異点問題を解決するために、WeChat ビジュアル チームは中山大学と協力し、双方から綿密な調査を実施しました。理論的および実践的な側面。まず、チームは、特異点の瞬間における逆過程の近似ガウス分布を含む誤差上限を提案しました。これは、その後の研究に理論的基礎を提供しました。この理論的保証に基づいて、チームは特異点でのサンプリングを研究し、2 つの重要な結論に達しました。1) t=1 の特異点は、極限を見つけることで分離可能な特異点に変換できる、2) t=0 での特異点これは拡散モデルの固有の特性であり、回避する必要はありません。これらの結論に基づいて、チームは初期瞬間における拡散モデルのサンプリングの問題を解決するためのプラグアンドプレイ手法 SingDiffusion を提案しました。 多数の実験検証により、SingDiffusion モジュールは 1 回のトレーニングだけで既存の拡散モデルにシームレスに適用でき、平均グレー値の問題が大幅に解決されることが示されています。 。 SingDiffusion は、分類子を使用しないガイダンス技術を使用せずに、現在の手法の生成品質を大幅に向上させることができ、特に Stable Diffusion1.5 (SD-1.5) に適用した後は、生成される画像の品質が 33% 向上しました。  論文アドレス: https://arxiv.org/pdf/2403.08381.pdfプロジェクト アドレス: https://pangzecheung.github.io/ SingDiffusion /論文タイトル: 拡散モデルにおける時間間隔の終点における特異点への取り組み
論文アドレス: https://arxiv.org/pdf/2403.08381.pdfプロジェクト アドレス: https://pangzecheung.github.io/ SingDiffusion /論文タイトル: 拡散モデルにおける時間間隔の終点における特異点への取り組み逆過程のガウス特性
#拡散モデルの特異点問題を検討するには、特異点での逆過程を含む過程全体がガウス性を満たしていることを検証する必要があります。まず
を拡散モデルのトレーニング サンプルとして定義します。トレーニング サンプルの分布は次のように表現できます: 其中 δ 表示狄拉克函數。根據[1] 中連續時間擴散模型的定義,對於任兩個時刻0≤s,t≤1,正向過程可以表示為:##其中
, ,
, ,
, 隨著時間單調的從1 變化到0。考慮到剛剛定義的訓練樣本分佈,
隨著時間單調的從1 變化到0。考慮到剛剛定義的訓練樣本分佈, 的單時刻邊際機率密度可以表示為:
的單時刻邊際機率密度可以表示為:

由此,可以透過貝葉斯公式計算逆過程的條件分佈:

然而,經過的分佈是混合高斯分佈,難以用網路進行擬合。因此,主流的擴散模型通常假設這一分佈可以由單一高斯分佈來擬合。

#其中,
為了驗證這個假設,該研究在 Proposition 1 中估計了此擬合的誤差。 

然而,研究發現當 t=1 時,隨著 s 趨近 1,
也會趨近於 1,誤差無法忽略。因此,Proposition 1 並不能證明 t=1 時的逆高斯特性。為了解決這個問題,研究給出了新的命題:
 命題 2 によれば、t=1 のとき、s が 1 に近づくにつれて
命題 2 によれば、t=1 のとき、s が 1 に近づくにつれて  は 0 に近づきます。したがって、本研究は特異点モーメントを含む逆過程全体がガウス特性に従うことを証明した。 逆関数のガウス特性の保証付きこの研究では、逆サンプリング公式に基づいて特異点モーメントのサンプリングを研究します。 まず、時間 t=1 における特異点の問題を考えます。 t=1、
は 0 に近づきます。したがって、本研究は特異点モーメントを含む逆過程全体がガウス特性に従うことを証明した。 逆関数のガウス特性の保証付きこの研究では、逆サンプリング公式に基づいて特異点モーメントのサンプリングを研究します。 まず、時間 t=1 における特異点の問題を考えます。 t=1、 =0 の場合、次のサンプリング式では分母が 0 で除算されます:
=0 の場合、次のサンプリング式では分母が 0 で除算されます:

研究チームは、極限を計算することで、特異値が得られることを発見しました。 point これは非特異点に変換できます: 
ただし、この制限はテスト中に計算できません。この目的を達成するために、この研究では、時間 t=1 で  をフィッティングし、「x - 予測」を使用して初期特異点でのサンプリング問題を解くことを提案します。 次に、時刻 t=0 を考えます。ガウス分布フィッティングの逆プロセスは、分散 0 のガウス分布、つまりディラック関数になります。 ## #### #########で###。このような特異点により、サンプリング プロセスが正しいデータ
をフィッティングし、「x - 予測」を使用して初期特異点でのサンプリング問題を解くことを提案します。 次に、時刻 t=0 を考えます。ガウス分布フィッティングの逆プロセスは、分散 0 のガウス分布、つまりディラック関数になります。 ## #### #########で###。このような特異点により、サンプリング プロセスが正しいデータ に収束します。したがって、t=0 での特異点は拡散モデルの優れた特性であり、回避する必要はありません。

 さらに、この調査では、付録で DDIM、SDE、および ODE の特異点の問題についても調査しています。
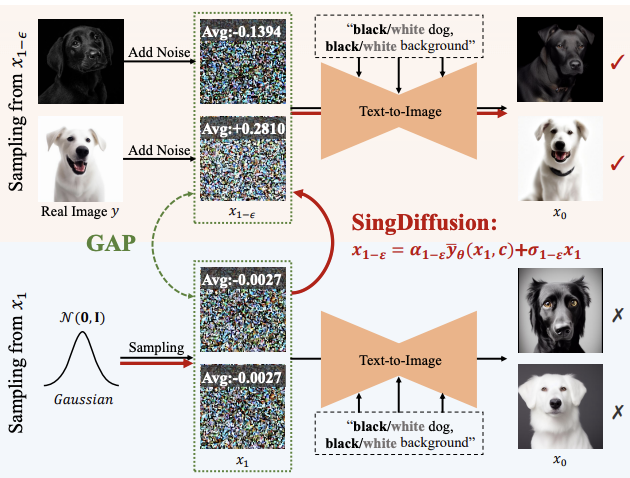
さらに、この調査では、付録で DDIM、SDE、および ODE の特異点の問題についても調査しています。  プラグアンドプレイ SingDiffusion モジュール特異点でのサンプリングは、拡散モデルによって生成された画像。たとえば、高輝度または低輝度のキューを入力する場合、既存の方法では多くの場合、平均グレースケールの画像しか生成できません。これは、平均グレースケール問題と呼ばれます。この問題は、既存の方法が t=0 の特異点でのサンプリングを無視し、1-ϵ の瞬間でのサンプリングの初期分布として 標準ガウス分布
プラグアンドプレイ SingDiffusion モジュール特異点でのサンプリングは、拡散モデルによって生成された画像。たとえば、高輝度または低輝度のキューを入力する場合、既存の方法では多くの場合、平均グレースケールの画像しか生成できません。これは、平均グレースケール問題と呼ばれます。この問題は、既存の方法が t=0 の特異点でのサンプリングを無視し、1-ϵ の瞬間でのサンプリングの初期分布として 標準ガウス分布 を使用するという事実に起因します。ただし、上の図に示すように、標準のガウス分布と 1-ϵ 時間の実際のデータ分布の間には大きなギャップがあります。
以上がCVPR 2024|非常に強い光で画像を生成できないのですか? WeChatビジョンチームが拡散モデルの特異点問題を効果的に解決の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

 論文アドレス: https://arxiv.org/pdf/2403.08381.pdf
論文アドレス: https://arxiv.org/pdf/2403.08381.pdf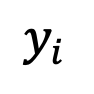
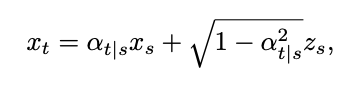
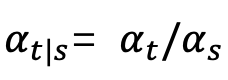 ,
,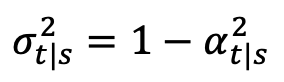 ,
,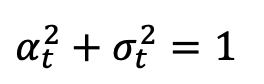 隨著時間單調的從1 變化到0。考慮到剛剛定義的訓練樣本分佈,
隨著時間單調的從1 變化到0。考慮到剛剛定義的訓練樣本分佈,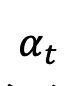 的單時刻邊際機率密度可以表示為:
的單時刻邊際機率密度可以表示為: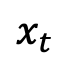
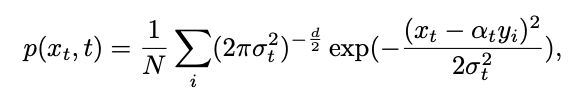
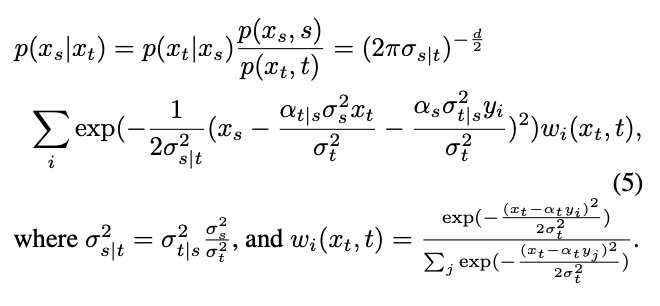
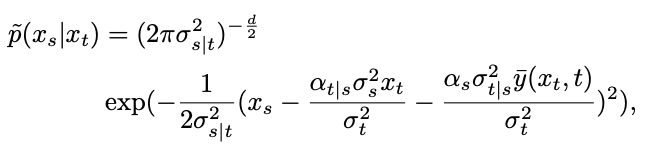
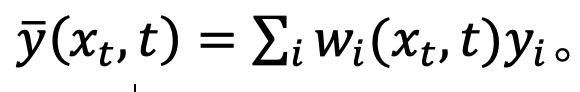
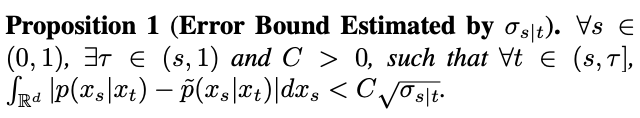
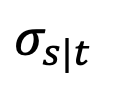
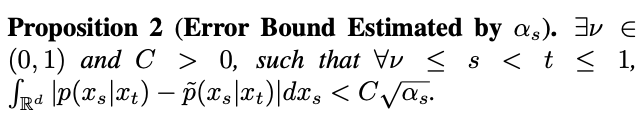
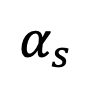 は 0 に近づきます。したがって、本研究は特異点モーメントを含む逆過程全体がガウス特性に従うことを証明した。
は 0 に近づきます。したがって、本研究は特異点モーメントを含む逆過程全体がガウス特性に従うことを証明した。  =0 の場合、次のサンプリング式では分母が 0 で除算されます:
=0 の場合、次のサンプリング式では分母が 0 で除算されます: 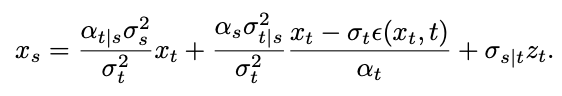
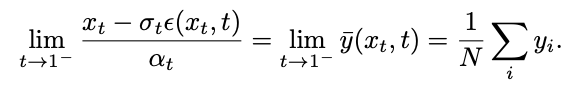
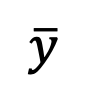 をフィッティングし、「x - 予測」を使用して初期特異点でのサンプリング問題を解くことを提案します。
をフィッティングし、「x - 予測」を使用して初期特異点でのサンプリング問題を解くことを提案します。 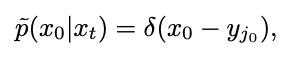
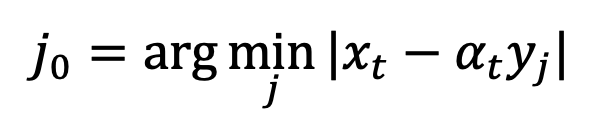 さらに、この調査では、付録で DDIM、SDE、および ODE の特異点の問題についても調査しています。
さらに、この調査では、付録で DDIM、SDE、および ODE の特異点の問題についても調査しています。 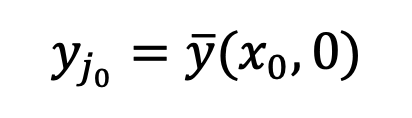

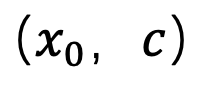 の場合、このメソッドは
の場合、このメソッドは 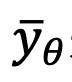 に適合するように Unet
に適合するように Unet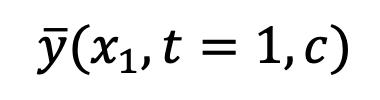 をトレーニングします。損失関数は次のように表されます。
をトレーニングします。損失関数は次のように表されます。 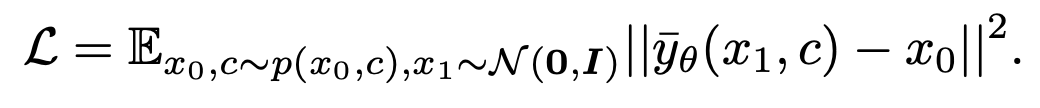
 sampling
sampling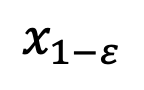 を使用できます。
を使用できます。 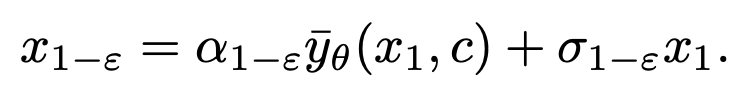
 が 1-ε 時点でのデータ分布
が 1-ε 時点でのデータ分布 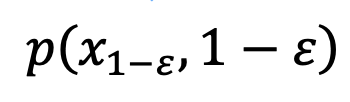 に確実に適合するようにし、それによって平均グレースケールの問題を解決します。このステップの後、事前トレーニングされたモデルを使用して、
に確実に適合するようにし、それによって平均グレースケールの問題を解決します。このステップの後、事前トレーニングされたモデルを使用して、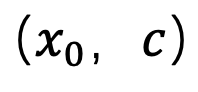 が生成されるまで後続のサンプリング ステップを実行できます。このメソッドはサンプリングの最初のステップにのみ関与し、その後のサンプリング プロセスとは何の関係もないため、SingDiffusion はほとんどの既存の拡散モデルに適用できることに注意してください。さらに、分類子ガイダンス操作がないことによって引き起こされるデータ オーバーフローの問題を回避するために、このメソッドは次の正規化操作も使用します。
が生成されるまで後続のサンプリング ステップを実行できます。このメソッドはサンプリングの最初のステップにのみ関与し、その後のサンプリング プロセスとは何の関係もないため、SingDiffusion はほとんどの既存の拡散モデルに適用できることに注意してください。さらに、分類子ガイダンス操作がないことによって引き起こされるデータ オーバーフローの問題を回避するために、このメソッドは次の正規化操作も使用します。 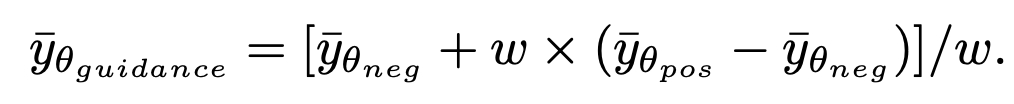
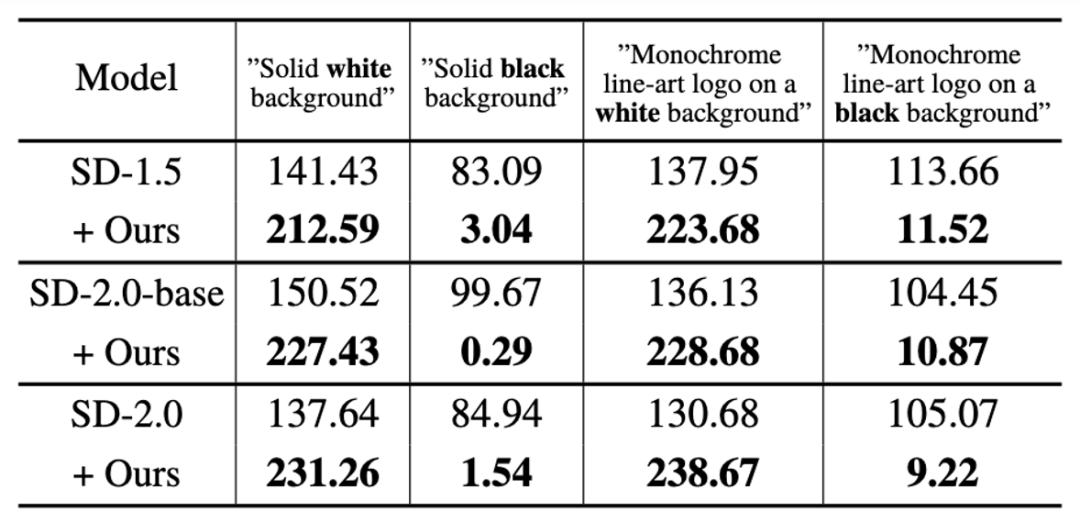


 この研究で提案された方法は 1 回のトレーニングのみを必要とし、既存の拡散モデルに簡単に適用して平均グレースケール問題を解決できることがわかります。
この研究で提案された方法は 1 回のトレーニングのみを必要とし、既存の拡散モデルに簡単に適用して平均グレースケール問題を解決できることがわかります。 