北京大学の林周晨氏のチームは、一次最適化アルゴリズムに触発されて、普遍的な近似特性を備えたニューラル ネットワーク アーキテクチャの設計方法を提案しました。
ニューラル ネットワークは、深層学習テクノロジーの基礎として、多くの応用分野で効果的な成果を上げています。実際には、ネットワーク アーキテクチャは学習効率に大きな影響を与える可能性があります。優れたニューラル ネットワーク アーキテクチャは、問題に関する事前知識を組み込み、ネットワーク トレーニングを確立し、コンピューティング効率を向上させることができます。現在、古典的なネットワーク アーキテクチャ設計手法には、手動設計、ニューラル ネットワーク アーキテクチャ検索 (NAS) [1]、および最適化ベースのネットワーク設計手法 [2] が含まれます。 ResNet などの人工的に設計されたネットワーク アーキテクチャ。ニューラル ネットワーク アーキテクチャの検索は、検索または強化学習を通じて最適なネットワーク構造を検索します。最適化ベースの設計手法の主流のパラダイムは、通常、ネットワークを設計します。明示的な目的関数を使用した最適化アルゴリズムの観点から構造を説明します。 これらの手法は、最適化アルゴリズムの観点からネットワーク構造を設計すると同時に、最適化アルゴリズムの観点からネットワーク構造を設計します。
現在の古典的なニューラル ネットワーク アーキテクチャ設計のほとんどは、ネットワークの普遍的な近似を無視しています。これは、ニューラル ネットワークの強力なパフォーマンスの重要な要素の 1 つです。したがって、これらの設計方法では、ネットワークのアプリオリな性能保証がある程度失われます。 2 層ニューラル ネットワークは、幅が無限大になる傾向がある場合に普遍的な近似特性を備えていますが [3]、実際には、通常、限られた幅のネットワーク構造のみを考慮することができ、この領域でのパフォーマンス解析の結果は非常に限られています。実際、ヒューリスティック人工設計であろうと、ブラックボックス ニューラル ネットワーク アーキテクチャの探索であろうと、ネットワーク設計において普遍的な近似特性を考慮することは困難です。最適化ベースのニューラル ネットワーク設計は比較的解釈しやすいですが、通常は明確な目的関数が必要となるため、設計されるネットワーク構造の種類が限られ、適用範囲が制限されます。普遍的な近似特性を備えたニューラル ネットワーク アーキテクチャを体系的に設計する方法は依然として重要な問題です。
北京大学の Lin Zhouchen 教授のチームは、最適化アルゴリズム設計ツールに基づいたニューラル ネットワーク アーキテクチャを提案しました。この手法は、勾配ベースの一次最適化アルゴリズムとハッシュ ベースの最適化アルゴリズムを組み合わせたものです。二次最適化。アルゴリズムを組み合わせることで、トレーニング速度と収束パフォーマンスが向上し、ニューラル ネットワークの堅牢性の保証が強化されます。このニューラル ネットワーク モジュールは、既存のモジュールベースのネットワーク設計手法でも使用でき、モデルのパフォーマンスを向上させ続けます。最近では、ニューラル ネットワーク微分方程式 (NODE) の近似特性を解析し、層間接続されたニューラル ネットワークが普遍的な近似特性を持つことを証明しました。また、提案されたフレームワークを ConvNext や ViT などのバリアント ネットワークの設計に使用し、成果を上げました。ベースラインを超えました。この論文は、人工知能のトップジャーナルである TPAMI に受理されました。

- 論文: 普遍的に近似するディープ ニューラル ネットワークの設計: 一次最適化アプローチ # #論文アドレス: https://ieeexplore.ieee.org/document/10477580
従来型ベースの最適化されたニューラルネットワーク設計手法は、多くの場合、明示的な式を使用した目的関数から開始し、特定の最適化アルゴリズムを使用してそれを解決し、その後、最適化結果をニューラル ネットワーク構造にマッピングします。たとえば、有名な LISTA-NN は、LISTA アルゴリズムを使用して、 LASSO 問題。結果として得られる明示的な式は、最適化の結果をニューラル ネットワーク構造に変換します [4]。この方法は目的関数の明示的な表現に強く依存するため、結果として得られるネットワーク構造は目的関数の明示的な表現に対してしか最適化できず、実際の状況に適合しない仮定を設計する危険性があります。 目的関数をカスタマイズしたり、アルゴリズム拡張などの手法を用いてネットワーク構造を設計しようとする研究者もいますが、重みの再結合などの仮定も必要となり、実際の状況では必ずしもその仮定を満たさない可能性があります。したがって、一部の研究者は、ニューラル ネットワークに基づく進化的アルゴリズムを使用してネットワーク アーキテクチャを探索し、より合理的なネットワーク構造を取得することを提案しています。
ネットワーク アーキテクチャ設計スキームの更新形式は、一次最適化アルゴリズムから近接点アルゴリズムまでの考え方に従い、段階的な最適化を実行する必要があります。たとえば、オイラー角アルゴリズムを四元数アルゴリズムに変更したり、より効率的な反復アルゴリズムを使用して解を近似したりできます。更新された形式では、計算精度の向上と運用効率の向上を考慮する必要があります。
ここで、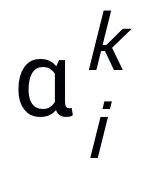 と
と 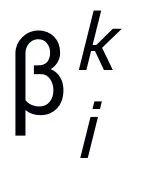 は k 番目のステップ更新時の (ステップ長) 係数を表し、勾配項をニューラル ネットワーク内の学習可能なモジュール T に置き換えます。 L 層ニューラル ネットワークのスケルトンを取得します。
は k 番目のステップ更新時の (ステップ長) 係数を表し、勾配項をニューラル ネットワーク内の学習可能なモジュール T に置き換えます。 L 層ニューラル ネットワークのスケルトンを取得します。
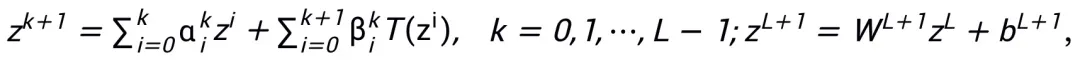
全体的なメソッドのフレームワークを図 1 に示します。
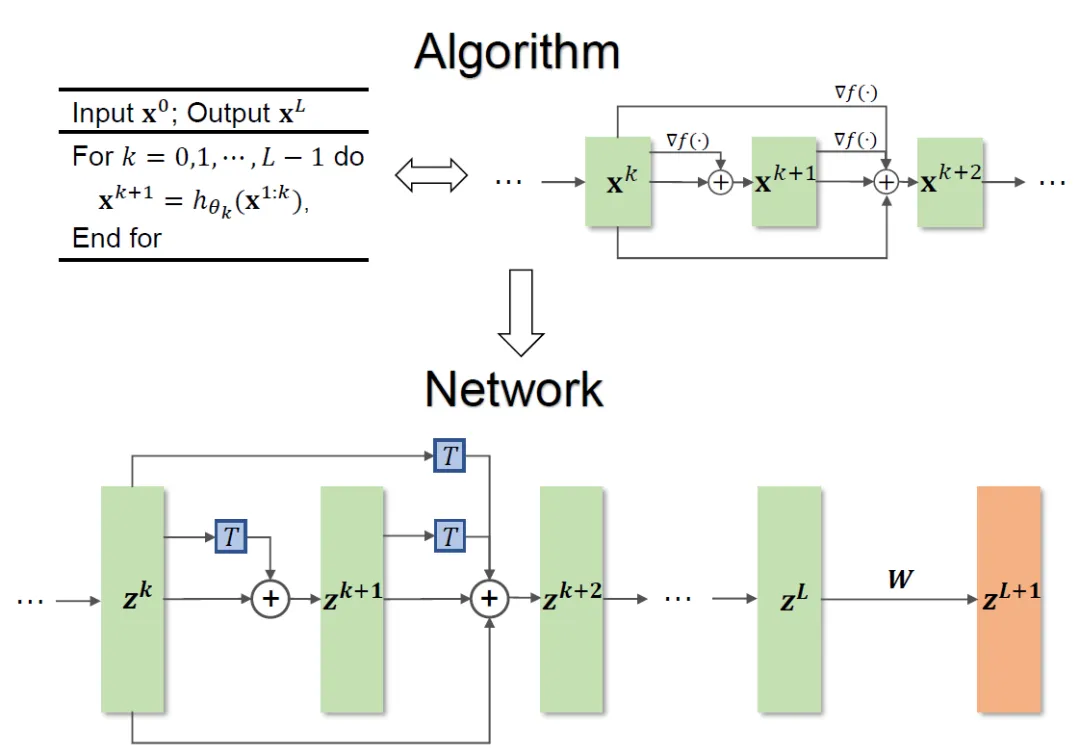
#図 1 ネットワーク設計図
この論文で提案されている方法は、ResNet の設計にインスピレーションを与えることができます。 、DenseNet などの古典的なネットワークであり、ネットワーク アーキテクチャの最適化設計に基づく従来の手法が特定の目的関数に限定されるという問題を解決します。
モジュールの選択とアーキテクチャの詳細
この方法で設計されたネットワーク モジュール T には、2 層ネットワークのみが必要です構造、つまり 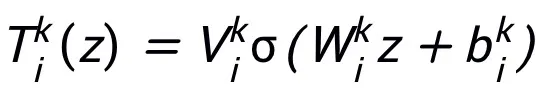 をその下部構造として使用すると、設計されたネットワークが普遍的な近似特性を持つことを保証できます。この特性では、表現される層の 幅が制限されます (つまり、ランダムではなく(近似精度の向上とともに増加します)、
をその下部構造として使用すると、設計されたネットワークが普遍的な近似特性を持つことを保証できます。この特性では、表現される層の 幅が制限されます (つまり、ランダムではなく(近似精度の向上とともに増加します)、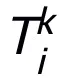 層を広げることでネットワーク全体の普遍的な近似特性が得られるわけではありません。モジュール T は、ResNet で広く使用されている事前アクティベーション ブロックにすることも、Transformer のアテンション フィードフォワード層の構造にすることもできます。 T の活性化関数には、ReLU、GeLU、Sigmoid などの一般的な活性化関数を使用できます。特定のタスクに応じて、対応する正規化レイヤーを追加することもできます。さらに、
層を広げることでネットワーク全体の普遍的な近似特性が得られるわけではありません。モジュール T は、ResNet で広く使用されている事前アクティベーション ブロックにすることも、Transformer のアテンション フィードフォワード層の構造にすることもできます。 T の活性化関数には、ReLU、GeLU、Sigmoid などの一般的な活性化関数を使用できます。特定のタスクに応じて、対応する正規化レイヤーを追加することもできます。さらに、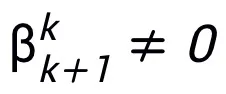 の場合、設計されたネットワークは陰的ネットワーク [5] であり、固定小数点反復法を使用して陰的形式を近似することも、陰的微分法を使用して勾配を解くこともできます。
の場合、設計されたネットワークは陰的ネットワーク [5] であり、固定小数点反復法を使用して陰的形式を近似することも、陰的微分法を使用して勾配を解くこともできます。
#等価表現によるより多くのネットワークの設計
この方法では、同じアルゴリズムが 1 つのみに対応する必要はありません。それとは対照的に、構造では、この方法は最適化問題の同等の表現を使用して、その柔軟性を反映してより多くのネットワーク アーキテクチャを設計できます。たとえば、線形化された交互方向乗算法は、制約付きの最適化問題を解決するためによく使用されます。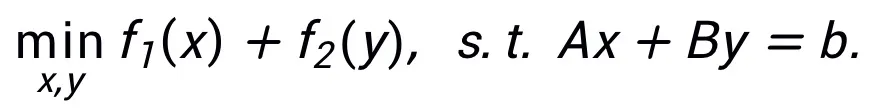
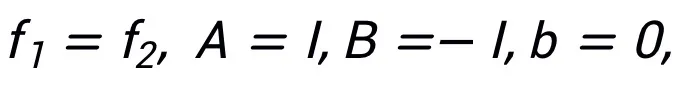 #着想を得たネットワーク構造を図 2 に示します。 。
#着想を得たネットワーク構造を図 2 に示します。 。
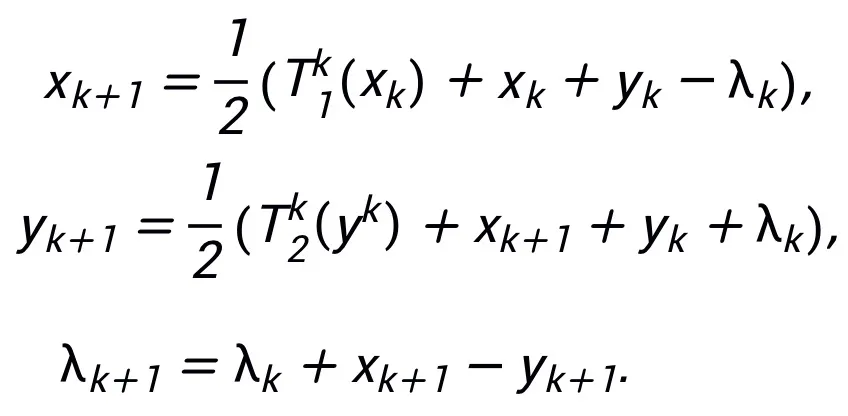
インスピレーションネットワーク普遍的な近似特性を持つ
この方法で設計されたネットワーク アーキテクチャは、モジュールが前述の条件を満たし、最適化アルゴリズム (一般に) が安定して収束するという条件下で、ニューラル ネットワークが一次最適化からインスピレーションを得たものであることを証明できます。アルゴリズムは高次元で実行できます。 連続関数空間は普遍的な近似特性を持ち、近似速度が与えられます。この論文は、制限された幅設定の下で一般的な層間接続を備えたニューラル ネットワークの普遍的な近似特性を初めて証明しました (以前の研究は基本的に FCNN と ResNet に焦点を当てていました。主定理を参照)。この論文の内容は次のように簡単に説明できます:
主定理 (短縮版): 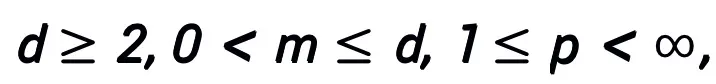 A ## と仮定します。 # は勾配型一次最適化アルゴリズムです。アルゴリズム A が式 (1) の更新形式を持ち、収束条件を満たす場合 (最適化アルゴリズムの一般的なステップ サイズの選択はすべて収束条件を満たします。それらがすべてヒューリスティック ネットワークで学習可能であれば、この条件は必要ありません)、アルゴリズムに触発されたニューラル ネットワーク:
A ## と仮定します。 # は勾配型一次最適化アルゴリズムです。アルゴリズム A が式 (1) の更新形式を持ち、収束条件を満たす場合 (最適化アルゴリズムの一般的なステップ サイズの選択はすべて収束条件を満たします。それらがすべてヒューリスティック ネットワークで学習可能であれば、この条件は必要ありません)、アルゴリズムに触発されたニューラル ネットワーク:
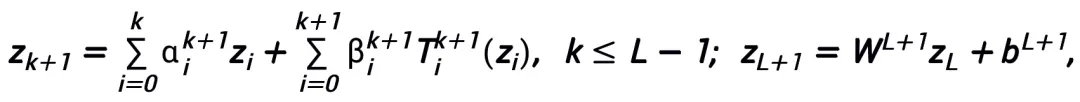
連続 (ベクトル値) 関数空間で 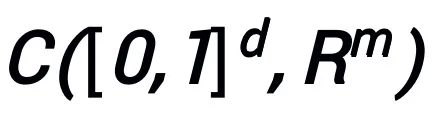 # そしてこれは、ノルム
# そしてこれは、ノルム 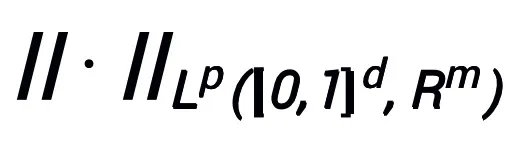 の下で普遍的な近似特性を持ちます。学習可能なモジュール T には、形式
の下で普遍的な近似特性を持ちます。学習可能なモジュール T には、形式  の 2 層構造が含まれているだけで済みます (σ は一般的に活性化関数 ) をその部分構造として使用しました。
の 2 層構造が含まれているだけで済みます (σ は一般的に活性化関数 ) をその部分構造として使用しました。
一般的に使用される T 構造は次のとおりです:
1) 畳み込みネットワークでは、事前アクティブ化ブロック: BN-ReLU-Conv-BN -ReLU -Conv (z),
##2) Transformer: Attn (z) MLP (z Attn (z)).の証明主定理は、NODE の普遍的な近似特性と線形マルチステップ法の収束特性を利用し、最適化アルゴリズムによって触発されたネットワーク構造が収束線形マルチステップによる連続 NODE の離散化に対応することを証明することです。 step メソッドにより、インスピレーションを受けたネットワークが NODE の近似機能を「継承」します。証明では、この論文は、d 次元空間で連続関数を近似するための NODE の近似速度も示し、前の論文 [6] の残された問題を解決します。
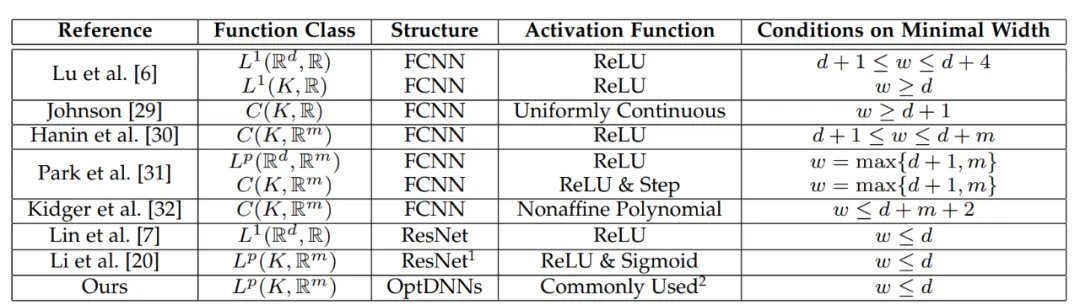 #表 1 ユニバーサル近似の特性に関するこれまでの研究は、基本的に FCNN と ResNet に焦点を当てていました。
#表 1 ユニバーサル近似の特性に関するこれまでの研究は、基本的に FCNN と ResNet に焦点を当てていました。
実験的結果
この論文では、提案されたネットワーク アーキテクチャ設計フレームワークを使用して、8 つの明示的ネットワークと 3 つの暗黙的ネットワーク (OptDNN と呼ばれます) を設計します。ネットワーク情報は表 2 に示されており、実験にネストされています。リング分離、関数近似、画像分類などの問題について研究が行われました。また、この論文では、ResNet、DenseNet、ConvNext、ViT をベースラインとして使用し、提案された方法を使用して改良された OptDNN を設計し、精度と FLOP の 2 つの指標を考慮して画像分類の問題に関する実験を行っています。
#表 2 設計したネットワークの関連情報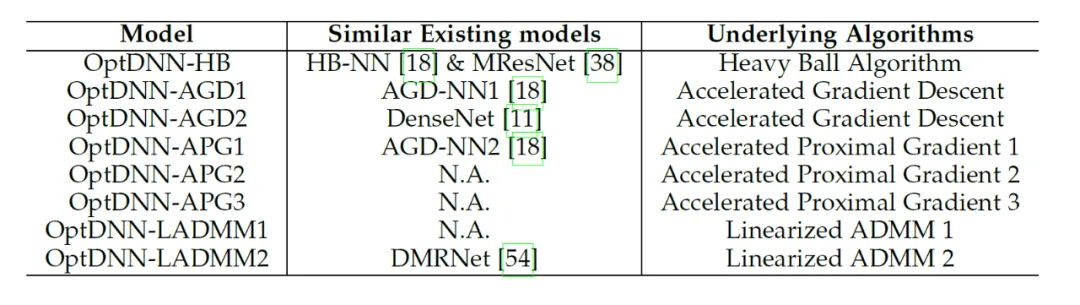
まず、OptDNN を分離し、実験を行います。関数近似の 2 つの問題を取り上げて、その普遍的な近似特性を検証します。関数近似問題では、近似パリティ関数とタルガースキー関数がそれぞれ考慮され、前者は二値分類問題として表現でき、後者は回帰問題として表されます。どちらも浅いネットワークで近似するのは困難です。ネストリング分離における OptDNN の実験結果を図 3 に、関数近似における実験結果を図 3 に示します。OptDNN は良好な分離/近似結果を達成しただけでなく、ベースラインとしての ResNet よりも優れた結果も達成しました。分類間隔とより小さい回帰誤差は、OptDNN の普遍的な近似特性を検証するのに十分です。
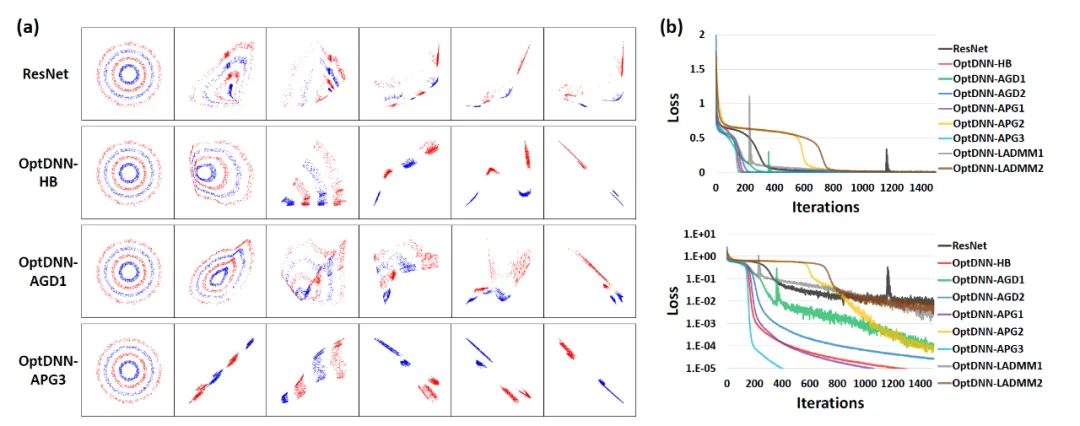
#図 3 OptNN 近似パリティ関数
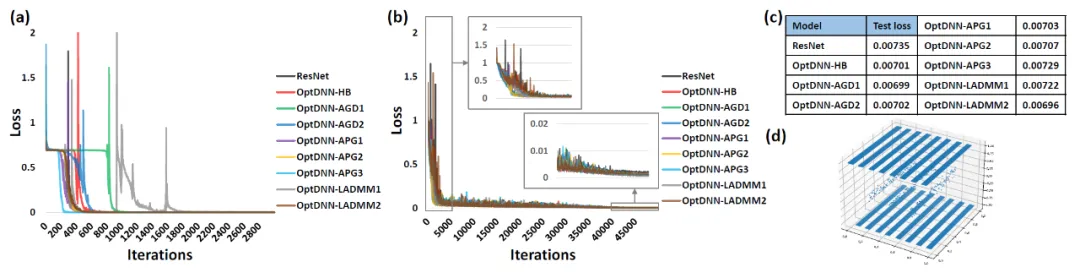
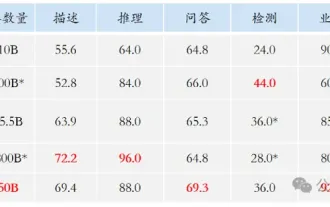
#次に、OptDNN は、広い - 浅い、狭い - 深いという 2 つの設定で CIFAR データ セットの画像分類タスクの実験を実施しました。結果は表を参照してください。 3と4。実験はすべて、強力なデータ拡張設定の下で実施され、一部の OptDNN は同じまたはさらに小さい FLOP オーバーヘッドで ResNet よりも低いエラー率を達成したことがわかります。この論文では、ResNet および DenseNet 設定下でも実験を実施し、同様の実験結果を達成しました。
#表 3 広く浅い設定での OptDNN の実験結果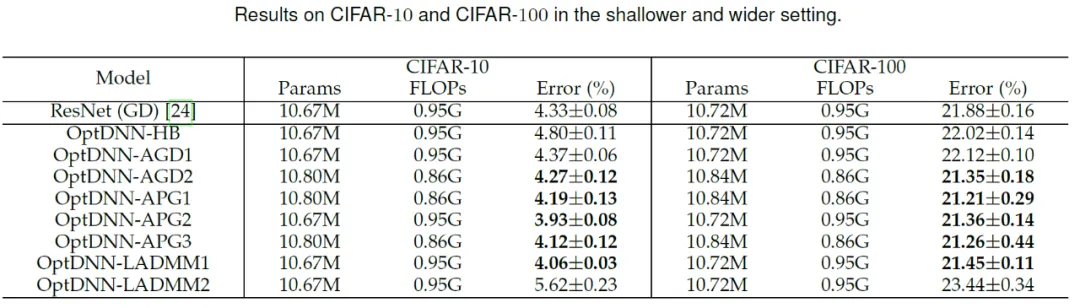
##表 4 ナローディープ設定での OptDNN の実験結果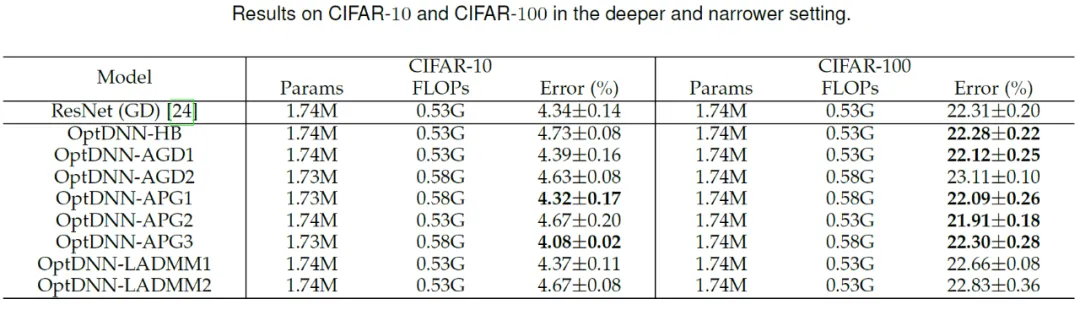
この論文では、以前に優れたパフォーマンスを発揮した OptDNN-APG2 ネットワークをさらに選択し、ConvNext と ViT のパフォーマンスをさらに向上させています。以下の設定で ImageNet データセットに対して実験を実施しました。OptDNN-APG2 のネットワーク構造を図 5 に示し、実験結果を表 5 および表 6 に示します。 OptDNN-APG2 は、等幅 ConvNext および ViT を超える精度率を達成し、このアーキテクチャ設計手法の信頼性がさらに実証されました。
#図 5 OptDNN-APG2 のネットワーク構造
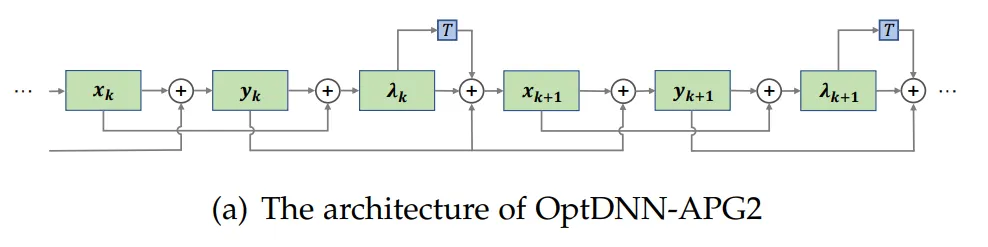
表 5 ImageNet での OptDNN-APG2 のパフォーマンス比較
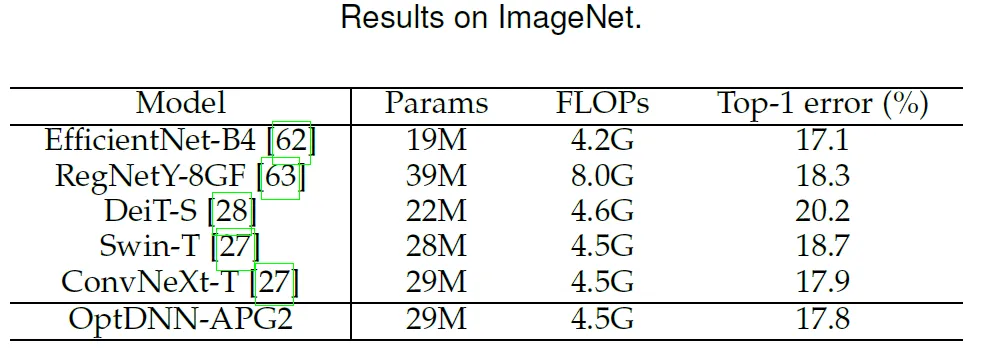
表 6 OptDNN-APG2 と等方性 ConvNeXt および ViT のパフォーマンス比較
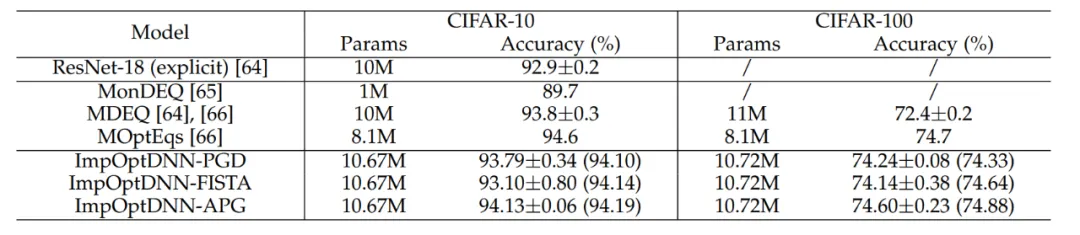
最後に、この論文では、近接勾配降下法や FISTA などのアルゴリズムに基づいて 3 つの陰的ネットワークを設計し、陽的 ResNet といくつかの一般的に使用される陰的ネットワークを使用した CIFAR データセットで実験を実施しました。実験結果は次のとおりです。表 7 に示します。 3 つの暗黙的ネットワークはすべて、高度な暗黙的ネットワークと同等の実験結果を達成しました。これは、手法の柔軟性も示しています。
#表 7 暗黙的ネットワークのパフォーマンスの比較
##ニューラル ネットワーク アーキテクチャの設計は、深層学習における中心的な問題の 1 つです。この論文では、一次最適化アルゴリズムを使用して普遍的な近似特性を持つニューラル ネットワーク アーキテクチャを設計するための統一フレームワークを提案し、最適化設計ネットワーク アーキテクチャ パラダイムに基づいてその方法を拡張します。この方法は、ネットワーク モジュールに焦点を当てたほとんどの既存のアーキテクチャ設計方法と組み合わせることができ、計算量をほとんど増加させることなく効率的なモデルを設計できます。理論の面では、この論文は、収束最適化アルゴリズムによって引き起こされるネットワーク アーキテクチャが穏やかな条件下で普遍的な近似特性を持ち、NODE と一般的な層間接続ネットワークの表現機能の橋渡しとなることを証明しています。この手法は、NAS、SNN アーキテクチャ設計などの分野と組み合わせて、より効率的なネットワーク アーキテクチャを設計することも期待されています。
以上が北京大学の林周晨氏のチームは、一次最適化アルゴリズムに触発されて、普遍的な近似特性を備えたニューラル ネットワーク アーキテクチャの設計方法を提案しました。の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7658
7658
 15
15
 1393
1393
 52
52
 91
91
 11
11
 38
38
 113
113
 オープンソース!ゾーイデプスを超えて! DepthFM: 高速かつ正確な単眼深度推定!
Apr 03, 2024 pm 12:04 PM
オープンソース!ゾーイデプスを超えて! DepthFM: 高速かつ正確な単眼深度推定!
Apr 03, 2024 pm 12:04 PM
0.この記事は何をするのですか?私たちは、多用途かつ高速な最先端の生成単眼深度推定モデルである DepthFM を提案します。従来の深度推定タスクに加えて、DepthFM は深度修復などの下流タスクでも最先端の機能を実証します。 DepthFM は効率的で、いくつかの推論ステップ内で深度マップを合成できます。この作品について一緒に読みましょう〜 1. 論文情報タイトル: DepthFM: FastMonocularDepthEstimationwithFlowMatching 著者: MingGui、JohannesS.Fischer、UlrichPrestel、PingchuanMa、Dmytr
 世界で最も強力なオープンソース MoE モデルが登場。GPT-4 に匹敵する中国語機能を備え、価格は GPT-4-Turbo のわずか 1% 近くです
May 07, 2024 pm 04:13 PM
世界で最も強力なオープンソース MoE モデルが登場。GPT-4 に匹敵する中国語機能を備え、価格は GPT-4-Turbo のわずか 1% 近くです
May 07, 2024 pm 04:13 PM
従来のコンピューティングを超える能力を備えているだけでなく、より低コストでより効率的なパフォーマンスを実現する人工知能モデルを想像してみてください。これは SF ではありません。世界で最も強力なオープンソース MoE モデルである DeepSeek-V2[1] が登場しました。 DeepSeek-V2 は、経済的なトレーニングと効率的な推論の特徴を備えた強力な専門家混合 (MoE) 言語モデルです。これは 236B のパラメータで構成されており、そのうち 21B は各マーカーをアクティブにするために使用されます。 DeepSeek67B と比較して、DeepSeek-V2 はパフォーマンスが優れていると同時に、トレーニング コストを 42.5% 節約し、KV キャッシュを 93.3% 削減し、最大生成スループットを 5.76 倍に高めます。 DeepSeek は一般的な人工知能を研究する会社です
 AI が数学研究を破壊する!フィールズ賞受賞者で中国系アメリカ人の数学者が上位 11 件の論文を主導 | テレンス・タオが「いいね!」しました
Apr 09, 2024 am 11:52 AM
AI が数学研究を破壊する!フィールズ賞受賞者で中国系アメリカ人の数学者が上位 11 件の論文を主導 | テレンス・タオが「いいね!」しました
Apr 09, 2024 am 11:52 AM
AI は確かに数学を変えつつあります。最近、この問題に細心の注意を払っている陶哲軒氏が『米国数学協会会報』(米国数学協会会報)の最新号を送ってくれた。 「機械は数学を変えるのか?」というテーマを中心に、多くの数学者が意見を述べ、そのプロセス全体は火花に満ち、ハードコアで刺激的でした。著者には、フィールズ賞受賞者のアクシャイ・ベンカテシュ氏、中国の数学者鄭楽軍氏、ニューヨーク大学のコンピューター科学者アーネスト・デイビス氏、その他業界で著名な学者を含む強力な顔ぶれが揃っている。 AI の世界は劇的に変化しています。これらの記事の多くは 1 年前に投稿されたものです。
 iPhoneのセルラーデータインターネット速度が遅い:修正
May 03, 2024 pm 09:01 PM
iPhoneのセルラーデータインターネット速度が遅い:修正
May 03, 2024 pm 09:01 PM
iPhone のモバイル データ接続に遅延や遅い問題が発生していませんか?通常、携帯電話の携帯インターネットの強度は、地域、携帯ネットワークの種類、ローミングの種類などのいくつかの要因によって異なります。より高速で信頼性の高いセルラー インターネット接続を実現するためにできることがいくつかあります。解決策 1 – iPhone を強制的に再起動する 場合によっては、デバイスを強制的に再起動すると、携帯電話接続を含む多くの機能がリセットされるだけです。ステップ 1 – 音量を上げるキーを 1 回押して放します。次に、音量小キーを押して、もう一度放します。ステップ 2 – プロセスの次の部分は、右側のボタンを押し続けることです。 iPhone の再起動が完了するまで待ちます。セルラーデータを有効にし、ネットワーク速度を確認します。もう一度確認してください 修正 2 – データ モードを変更する 5G はより優れたネットワーク速度を提供しますが、信号が弱い場合はより適切に機能します
 こんにちは、電気アトラスです!ボストン・ダイナミクスのロボットが復活、180度の奇妙な動きにマスク氏も恐怖
Apr 18, 2024 pm 07:58 PM
こんにちは、電気アトラスです!ボストン・ダイナミクスのロボットが復活、180度の奇妙な動きにマスク氏も恐怖
Apr 18, 2024 pm 07:58 PM
Boston Dynamics Atlas は正式に電動ロボットの時代に突入します!昨日、油圧式アトラスが歴史の舞台から「涙ながらに」撤退したばかりですが、今日、ボストン・ダイナミクスは電動式アトラスが稼働することを発表しました。ボストン・ダイナミクス社は商用人型ロボットの分野でテスラ社と競争する決意を持っているようだ。新しいビデオが公開されてから、わずか 10 時間ですでに 100 万人以上が視聴しました。古い人が去り、新しい役割が現れるのは歴史的な必然です。今年が人型ロボットの爆発的な年であることは間違いありません。ネットユーザーは「ロボットの進歩により、今年の開会式は人間のように見え、人間よりもはるかに自由度が高い。しかし、これは本当にホラー映画ではないのか?」とコメントした。ビデオの冒頭では、アトラスは仰向けに見えるように地面に静かに横たわっています。次に続くのは驚くべきことです
 MLP に代わる KAN は、オープンソース プロジェクトによって畳み込みまで拡張されました
Jun 01, 2024 pm 10:03 PM
MLP に代わる KAN は、オープンソース プロジェクトによって畳み込みまで拡張されました
Jun 01, 2024 pm 10:03 PM
今月初め、MIT やその他の機関の研究者らは、MLP に代わる非常に有望な代替案である KAN を提案しました。 KAN は、精度と解釈可能性の点で MLP よりも優れています。また、非常に少数のパラメーターを使用して、多数のパラメーターを使用して実行する MLP よりも優れたパフォーマンスを発揮できます。たとえば、著者らは、KAN を使用して、より小規模なネットワークと高度な自動化で DeepMind の結果を再現したと述べています。具体的には、DeepMind の MLP には約 300,000 個のパラメーターがありますが、KAN には約 200 個のパラメーターしかありません。 KAN は、MLP が普遍近似定理に基づいているのに対し、KAN はコルモゴロフ-アーノルド表現定理に基づいているのと同様に、強力な数学的基礎を持っています。以下の図に示すように、KAN は
 超知性の生命力が覚醒する!しかし、自己更新 AI の登場により、母親はデータのボトルネックを心配する必要がなくなりました。
Apr 29, 2024 pm 06:55 PM
超知性の生命力が覚醒する!しかし、自己更新 AI の登場により、母親はデータのボトルネックを心配する必要がなくなりました。
Apr 29, 2024 pm 06:55 PM
世界は狂ったように大きなモデルを構築していますが、インターネット上のデータだけではまったく不十分です。このトレーニング モデルは「ハンガー ゲーム」のようであり、世界中の AI 研究者は、データを貪欲に食べる人たちにどのように餌を与えるかを心配しています。この問題は、マルチモーダル タスクで特に顕著です。何もできなかった当時、中国人民大学学部のスタートアップチームは、独自の新しいモデルを使用して、中国で初めて「モデル生成データフィード自体」を実現しました。さらに、これは理解側と生成側の 2 つの側面からのアプローチであり、両方の側で高品質のマルチモーダルな新しいデータを生成し、モデル自体にデータのフィードバックを提供できます。モデルとは何ですか? Awaker 1.0 は、中関村フォーラムに登場したばかりの大型マルチモーダル モデルです。チームは誰ですか?ソフォンエンジン。人民大学ヒルハウス人工知能大学院の博士課程学生、ガオ・イージャオ氏によって設立されました。
 FisheyeDetNet: 魚眼カメラに基づいた最初のターゲット検出アルゴリズム
Apr 26, 2024 am 11:37 AM
FisheyeDetNet: 魚眼カメラに基づいた最初のターゲット検出アルゴリズム
Apr 26, 2024 am 11:37 AM
目標検出は自動運転システムにおいて比較的成熟した問題であり、その中でも歩行者検出は最も初期に導入されたアルゴリズムの 1 つです。ほとんどの論文では非常に包括的な研究が行われています。ただし、サラウンドビューに魚眼カメラを使用した距離認識については、あまり研究されていません。放射状の歪みが大きいため、標準のバウンディング ボックス表現を魚眼カメラに実装するのは困難です。上記の説明を軽減するために、拡張バウンディング ボックス、楕円、および一般的な多角形の設計を極/角度表現に探索し、これらの表現を分析するためのインスタンス セグメンテーション mIOU メトリックを定義します。提案された多角形モデルの FisheyeDetNet は、他のモデルよりも優れたパフォーマンスを示し、同時に自動運転用の Valeo 魚眼カメラ データセットで 49.5% の mAP を達成しました。




