
たとえば、台形 ABCD では、AD∥BC、AB=AD BC、E は CD の中点であることが知られています。証明: AE と BE はそれぞれ ∠BAD と ∠ABC を二等分します。
既知の条件から始めて、次の手順に従って、幾何学スケッチパッド上に質問の意味を満たす図を描きます。
幾何学的なスケッチパッドを開き、[点ツール]を使用してスケッチパッドの空白スペースに 2 つの点 A と B を描き、[光線ツール]を選択して点 A と点 B をそれぞれ通る水平線を描きます。点 A と B を選択して線分を作成します。
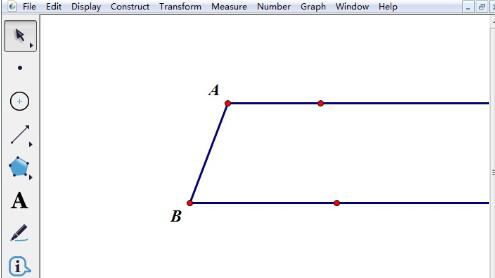
[ポイントツール]を使用して線分AB上の点Fを選択し、点AとBを中心点として、長さAFとBFを次のようにします。 2 つの底辺で円を描くための半径。光線は点 D と点 C で交差します。明らかに、AD BC=AB です。
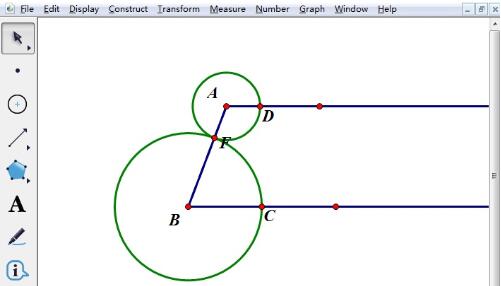
線分 CD の中点 E をとり、AE と BE を接続します。点CとDを選択し、[作図]-[中点]コマンドを実行して中点Eを描画し、点A、E、B、Eを順に選択し、[作図]-[線分]コマンドを実行して直線を取得します。セグメントAE、BE。
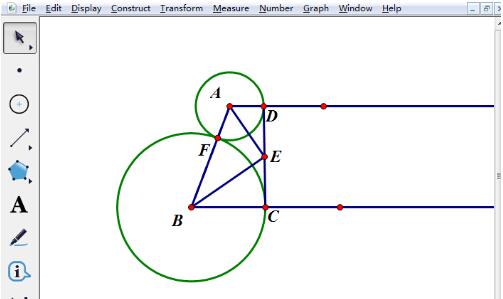
質問の要件を満たすグラフィックスを取得するには、描画プロセス中に補助グラフィックスを非表示にします。不要な光線と円を選択し、ショートカット キー [Ctrl H] を押すと不要なオブジェクトが非表示になり、図に示すように質問の意味を組み合わせたグラフィックが得られます。
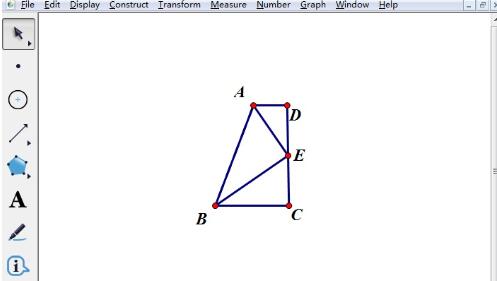
以上が幾何学スケッチパッドで既知の条件に従って幾何学図形を描画する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。