幾何学スケッチパッドに微分関数の画像を描画し、関数の極値を求める方法

描画する場合、関数の極値を見つけることが特に重要です。 Geometry Sketchpad は、微分関数のイメージに基づいて関数の極値を見つける方法を提供します。この方法は、単純な関数だけでなく、複雑な関数にも使用できます。誰もがこの方法を深く理解できるように、PHP エディターの Xinyi がその原理と手順を以下で詳しく説明します。

1. 幾何スケッチパッドを開き、[描画]-[新しい関数の描画]を開き、関数エディタに下図の関数解析式を入力し、[OK]をクリックします。

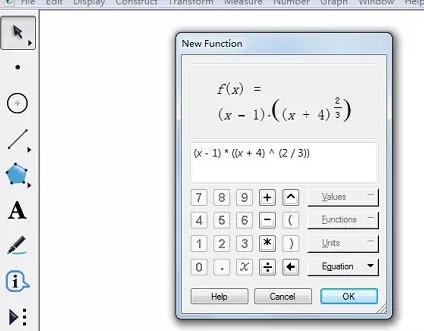
2. 関数の解析式を右クリックし、[微分関数の定義]を選択すると、微分関数の解析式が表示されます。微分関数を右クリックし、[関数描画]を選択すると、描画エリアに元の関数の微分関数(青色)が表示されます。

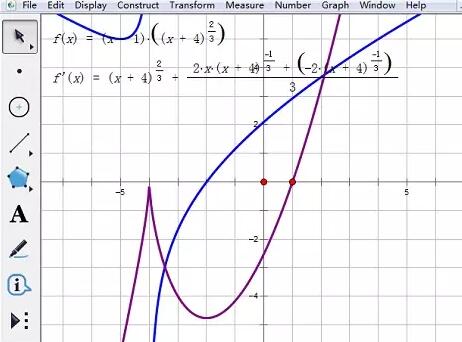
3. 描画した微分関数の画像とX軸を選択し、[作図]-[交点]を選択して点Aを取得します。元の関数は点Bで微分できないので、[描画]-[点の描画]で点B(-4,0)を描画します。

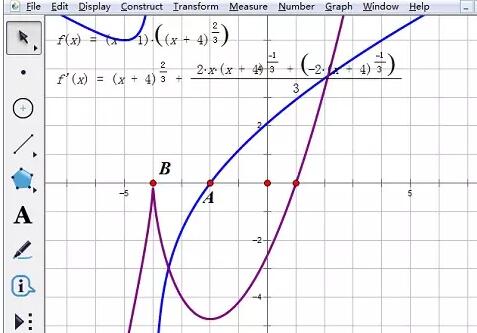
4. 点 B と点 A、[メトリック] - [横座標] を選択します。横座標の値は、元の関数の単調区間の転換点の横座標です。

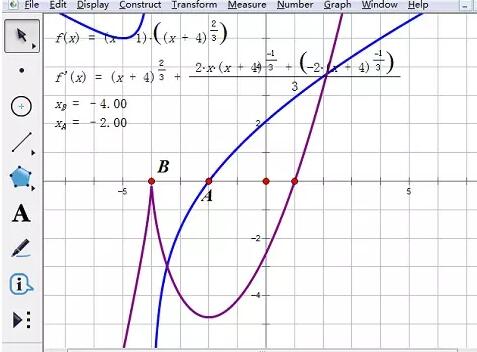
説明: 描画点 B には導関数が存在しないため、元の関数の点 B での最大値は 0、点 A での最小値になります。

以上が幾何学スケッチパッドに微分関数の画像を描画し、関数の極値を求める方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。