300 年以上にわたるリレー: テレンス・テルに触発されて、数学者たちは AI を使用してフェルマーの最終定理の証明を形式化することに決めました。
テレンス・タオに触発されて、数学的探求に人工知能を使用しようとする数学者が増えています。今回のターゲットは、世界トップ10に入る数学の難問「フェルマーの最終定理」。フェルマーの最終定理は非常に複雑な数学的問題であり、これまでのところ実現可能な解決策は見つかっていません。数学者は、人工知能の強力な計算能力とインテリジェントなアルゴリズムの助けを借りて、数学で探究できることを望んでいます

フェルマーの最終定理は、「フェルマーの最終定理」とも呼ばれます。 (FLT)」は、17 世紀のフランスの数学者ピエール・ド・フェルマーによって提唱されました。その背景には伝説的な物語があります。 1637 年頃、フェルマーがディオファントスの『算術』のラテン語訳を読んでいたとき、第 11 巻の命題 8 の隣に次のように書いたと言われています。 「私はこれについて何かを発見したと確信しています。これは素晴らしいデモンストレーションですが、残念ながら、ここの空白スペースは小さすぎて書き込むことができません。

#この段落の前に記載されているのは、フェルマーの最終定理の内容です。整数 n > 2 のとき、x^n y^n=z^n についての方程式が成り立ちます。
フェルマーはそれを証明する方法を知っていると述べましたが、本の空白部分が小さすぎるため、物語の信憑性やフェルマーが本当に理解したかどうかについては書きませんでした。この証明方法は後世で議論の的となっており、数学者たちは 1995 年まで 8 年間を費やしてフェルマーの最終定理を証明してきました。
 フェルマーの最終定理が証明されたので、数学者は AI で他に何ができるでしょうか? 答えは、その証明を形式化することです。
フェルマーの最終定理が証明されたので、数学者は AI で他に何ができるでしょうか? 答えは、その証明を形式化することです。
その背景や動機、具体的な方法をブログで紹介しました。
 なぜフェルマーの最終定理の証明を形式化する必要があるのでしょうか?
なぜフェルマーの最終定理の証明を形式化する必要があるのでしょうか?
アンドリュー ワイルズは FLT からインスピレーションを受けたかもしれませんが、実際、彼の研究はラングランズ プロジェクト、つまり数論、代数幾何学、近似を結びつけた数学における一連の広範囲にわたるアイデアに画期的な進歩をもたらしました。グループ代表者の割合は2024年になっても注目を集めています。
歴史的に、代数的整数論における他のいくつかの大きな進歩 (数体の因数分解や巡回体の算術など) は、少なくとも部分的には FLT をより深く理解したいという欲求によって動機付けられました。ワイルズの研究は、彼の生徒であるリチャード・テイラーによって補完され、20世紀の数学の広大な基礎の上に構築されました。ワイルズによって導入された基本的な手法である「モジュール性リフティング定理」は、元の論文が出版されてから 30 年間で概念的に大幅に簡略化され、広く一般化されました。この分野は現在でも非常に活発です。 2022 年の国際数学者会議でのフランク・カレガリの論文。ワイルズの躍進以来の進歩を概説しています (参照: https://arxiv.org/abs/2109.14145)。 Kevin Buzzard 氏は、この分野での継続的な活動が FLT 証明を形式化する動機の 1 つであると述べました。
数学の形式化とは、紙上の数学を、定理や証明の概念を理解できるようにするコンピューター プログラミング言語に変換する技術です。インタラクティブ定理証明器 (ITP) としても知られるこれらのプログラミング言語は、何十年も前から存在しています。しかし、近年、この分野は数学界からある程度の注目を集めているようです。私たちは数学における研究の形式化の例をいくつか目撃してきましたが、その最新のものは、テレンス・タオらによる多項式フライマン・ルザ予想の証明の形式化です。この 2023 年の画期的な論文は、わずか 3 週間で Lean で正式に作成されました。このような成功物語は、リーンのような ITP が今やすべての現代数学を形式化する準備ができていると傍観者に思わせるかもしれません。
しかし、真実は決して単純ではありません。組み合わせ論などの数学の一部の分野では、現代の画期的な進歩がリアルタイムで形式化されているのが見られます。しかし、バザード氏は定期的にロンドンの整数論セミナーに参加しており、現代の数学的定義に関するリーンの知識がセミナーで発表された結果を定式化するのに不十分であり、ましてやその証明を検証するのに不十分であることによく気づいたと述べた。
実際、この側面における数論の「遅れ」は、バザードが FLT の現代的な証明の形式化を開始する主な動機の 1 つでした。プロジェクトの終わりまでに、リーンは保型形式 (複素変数の関数の特別なクラス) と表現、ガロア表現、潜在自己同型、モジュール性推進定理、代数多様体の算術、クラス体理論、算術双対定理を理解できるようになります。 、志村多様体および現代の代数整数論で使用されるその他の概念。バザード氏の見解では、これらの基盤が整備されていれば、彼自身の専門分野で起こっていることを形式化することはもはやSFではなくなるでしょう。
それでは、なぜこれを行うのでしょうか?バザード氏は、「一部のコンピューター科学者が信じているのであれば、人工知能の急激な成長により、最終的にはコンピューターが数学者の研究を支援できるようになるだろう。そのような研究は、コンピューターが現代の数学研究で何をしているのかを理解するのに役立つだろう。」と説明した。
プロジェクトをどのように実行するか?フェルマーの最終定理の定式化プロジェクトが始動しました。 Buzzard は現在の進行状況をグラフィックで表示します。
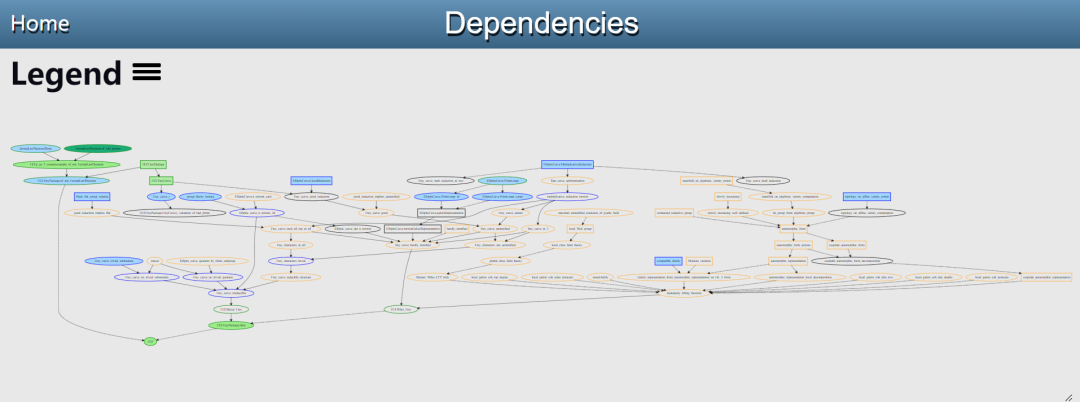 興味のある研究者は詳細を読むことができます: https:// Imperialcollegelondon.github.io/FLT/blueprint/dep_graph_document.html
興味のある研究者は詳細を読むことができます: https:// Imperialcollegelondon.github.io/FLT/blueprint/dep_graph_document.html
このプロジェクトは EPSRC によって後援されています。資金提供により、Buzzard は最初の 5 年間の資金を受け取ります。この期間における彼の最初の目標は、FLT を 1980 年代後半に数学者に知られていたステートメントに還元することでした。
もちろん、バザードは単独でこれを行うつもりはありませんでした。同氏は、議論の一部については基本原則は理解したが、詳細を詳しく検討したことはなかったと述べた。さらに、Project Langlands では、GL_2 の循環基底変換や Jacquet-Langlands など、いくつかの重要なことも導入されました。これらの奥深い事柄に対する彼の理解は十分に深くありません。
ただし、これこそが正式なプロジェクトの利点です。 Buzzard は、Lean で必要な結果を明確に表現し、他の人に伝えることができるようになります。このシステムの利点は、貢献するために FLT の証明全体を理解する必要がないことです。上の図は証明を多くの小さな補題に分割しているため、クラウドソーシングに非常に便利です。これらの補題のいずれかを正式に証明できれば、Buzzard はあなたのプル リクエストを心待ちにしています。
プロジェクトに参加したい人は、Lean について知っておく必要があります。このため、バザードはオンライン教科書 Mathematics in Lean を推奨しています。
 教科書リンク: https://leanprover-community.github.io/mathematics_in_lean/
教科書リンク: https://leanprover-community.github.io/mathematics_in_lean/
このプロジェクトは、Lean の FLT ストリームで実行されます。 Zulip チャットは、数学者とコンピューター科学者がリアルタイムで共同作業できる強力な研究フォーラムで、コードと数学を簡単に公開し、スレッドとストリーム システムを使用して複数の独立した会話を同時に効果的にサポートします。
 Lean Zulip チャット リンク: https://leanprover.zulipchat.com/
Lean Zulip チャット リンク: https://leanprover.zulipchat.com/
Buzzard 氏は、プロジェクトにどれくらいの時間がかかるかわからないと述べました。しかし彼は間違いなく楽観的だ。
同時に、Lean のような正式な証明ツールも常に反復されています。オリジナルの Lean と比較して、最新の Lean 4 バージョンでは、コンパイラの高速化、エラー処理の改善、外部ツールとの統合の改善など、多くの最適化が行われています。
昨年末、オープン プラットフォームの LeanDojo チームとカリフォルニア工科大学の研究者は、大規模な言語モデルが人間と対話できるように設計されたコラボレーション ツールである Lean Copilot を立ち上げ、数学的手法に AI を導入しました。大きなモデルの力。
「適切に使用すれば、AI は 2026 年までに数学研究や他の多くの分野で信頼できる共著者になると私は予測しています。」と Tao Zhexuan 氏は以前のブログで述べました。
テレンス・タオの予言が近いうちに当たることを願っています。
関連記事:
AI を使用したテレンス タオの正式な証明とは何ですか? PFR 予想の過去と現在を理解するための 1 つの記事>>
Tao Zhexuan のお気に入りの証明アシスタント Lean は大規模なモデルを使用しています>>
大きなモデルは、テレンス タオが問題を解決し、数学の定理を証明するのに役立ちます。本当に数学は、AI の助けを借りてブレークスルーを達成する最初の科目になるのでしょうか? 》
- ##《
Tao Zhexuan の新しいプロジェクト: Lean での素数定理の証明、研究青写真が完成しました 》
参考リンク: https://leanprover.zulipchat.com/#narrow/stream/416277-FLT
https : //mp.weixin.qq.com/s/d9RSkRhlKH5ZMek3yTqe4Q
以上が300 年以上にわたるリレー: テレンス・テルに触発されて、数学者たちは AI を使用してフェルマーの最終定理の証明を形式化することに決めました。の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 1663
1663
 14
14
 1420
1420
 52
52
 1315
1315
 25
25
 1266
1266
 29
29
 1239
1239
 24
24
 Gitプロジェクトをローカルにダウンロードする方法
Apr 17, 2025 pm 04:36 PM
Gitプロジェクトをローカルにダウンロードする方法
Apr 17, 2025 pm 04:36 PM
gitを介してローカルにプロジェクトをダウンロードするには、次の手順に従ってください。gitをインストールします。プロジェクトディレクトリに移動します。次のコマンドを使用してリモートリポジトリのクローニング:git clone https://github.com/username/repository-name.git
 gitでコードを更新する方法
Apr 17, 2025 pm 04:45 PM
gitでコードを更新する方法
Apr 17, 2025 pm 04:45 PM
GITコードを更新する手順:コードをチェックしてください:gitクローンhttps://github.com/username/repo.git最新の変更を取得:gitフェッチマージの変更:gitマージオリジン/マスタープッシュ変更(オプション):gitプッシュオリジンマスター
 PHPプロジェクトで効率的な検索問題を解決する方法は?タイプセンスはあなたがそれを達成するのに役立ちます!
Apr 17, 2025 pm 08:15 PM
PHPプロジェクトで効率的な検索問題を解決する方法は?タイプセンスはあなたがそれを達成するのに役立ちます!
Apr 17, 2025 pm 08:15 PM
eコマースのウェブサイトを開発するとき、私は困難な問題に遭遇しました:大量の製品データで効率的な検索機能を達成する方法は?従来のデータベース検索は非効率的であり、ユーザーエクスペリエンスが低いです。いくつかの調査の後、私は検索エンジンタイプセンスを発見し、公式のPHPクライアントタイプセンス/タイプセンス-PHPを通じてこの問題を解決し、検索パフォーマンスを大幅に改善しました。
 Gitダウンロードがアクティブでない場合はどうすればよいですか
Apr 17, 2025 pm 04:54 PM
Gitダウンロードがアクティブでない場合はどうすればよいですか
Apr 17, 2025 pm 04:54 PM
解決:gitのダウンロード速度が遅い場合、次の手順を実行できます。ネットワーク接続を確認し、接続方法を切り替えてみてください。 GIT構成の最適化:ポストバッファーサイズ(Git Config -Global HTTP.Postbuffer 524288000)を増やし、低速制限(GIT Config -Global HTTP.LowsPeedLimit 1000)を減らします。 Gitプロキシ(Git-ProxyやGit-LFS-Proxyなど)を使用します。別のGitクライアント(SourcetreeやGithubデスクトップなど)を使用してみてください。防火を確認してください
 gitコミットの使用方法
Apr 17, 2025 pm 03:57 PM
gitコミットの使用方法
Apr 17, 2025 pm 03:57 PM
GITコミットは、プロジェクトの現在の状態のスナップショットを保存するために、ファイルの変更をGITリポジトリに記録するコマンドです。使用方法は次のとおりです。一時的なストレージエリアに変更を追加する簡潔で有益な提出メッセージを書き込み、送信メッセージを保存して終了して送信を完了します。
 gitでコードをマージする方法
Apr 17, 2025 pm 04:39 PM
gitでコードをマージする方法
Apr 17, 2025 pm 04:39 PM
gitコードマージプロセス:競合を避けるために最新の変更を引き出します。マージするブランチに切り替えます。マージを開始し、ブランチをマージするように指定します。競合のマージ(ある場合)を解決します。ステージングとコミットマージ、コミットメッセージを提供します。
 Gitでローカルコードを更新する方法
Apr 17, 2025 pm 04:48 PM
Gitでローカルコードを更新する方法
Apr 17, 2025 pm 04:48 PM
ローカルGitコードを更新する方法は? Git Fetchを使用して、リモートリポジトリから最新の変更を引き出します。 Git Merge Origin/<リモートブランチ名>を使用して、地元のブランチへのリモート変更をマージします。合併から生じる競合を解決します。 Git Commit -M "Merge Branch< Remote Branch Name>"を使用してください。マージの変更を送信し、更新を適用します。
 GITでリポジトリを削除する方法
Apr 17, 2025 pm 04:03 PM
GITでリポジトリを削除する方法
Apr 17, 2025 pm 04:03 PM
gitリポジトリを削除するには、次の手順に従ってください。削除するリポジトリを確認します。リポジトリのローカル削除:RM -RFコマンドを使用して、フォルダーを削除します。倉庫をリモートで削除する:倉庫の設定に移動し、「倉庫の削除」オプションを見つけて、操作を確認します。




