MLPは一夜にして消滅した! MIT カリフォルニア工科大学とその他の革新的な KAN が記録を破り、DeepMind を打ち砕く数学的定理を発見
機械学習のパラダイムは一夜にして変わります。
今日、深層学習の分野を支配するインフラストラクチャは、ニューロンに活性化関数を配置する多層パーセプトロン (MLP) です。
それで、これ以外に何か新しいルートはあるでしょうか?


ちょうど今日、MIT、カリフォルニア工科大学、ノースイースタン大学、その他の機関のチームが、新しいニューラル ネットワーク構造、コルモゴロフ – アーノルド ネットワーク (KAN) をリリースしました。

研究者らは MLP に簡単な変更を加えました。つまり、学習可能な活性化関数をノード (ニューロン) からエッジ (重み) に移動しました。

論文アドレス: https://arxiv.org/pdf/2404.19756
この変更は一見根拠がないように思えるかもしれませんが、数学の「近似理論」とかなり深い関係があります。
コルモゴロフ-アーノルド表現は、ノードではなくエッジに学習可能な活性化関数を備えた 2 層ネットワークに対応していることがわかりました。
表現定理に触発されて、研究者はニューラル ネットワークを使用してコルモゴロフ-アーノルド表現を明示的にパラメータ化しました。
KAN という名前の由来は、故アンドレイ・コルモゴロフとウラジミール・アーノルドという二人の偉大な数学者を記念するものであることは言及する価値があります。

実験結果は、KANが従来のMLPより優れたパフォーマンスを持ち、ニューラルネットワークの精度と解釈可能性を向上させることを示しています。

最も予想外だったのは、KAN の視覚化とインタラクティブ性が科学研究における潜在的な応用価値をもたらし、科学者が新しい数学的および物理的法則を発見するのに役立つということです。
研究では、著者は KAN を使用して結び目理論の数学的法則を再発見しました。
さらに、KAN は、2021 年に、より小規模なネットワークと自動化を使用して DeepMind の結果を再現しました。

物理学では、KAN は物理学者がアンダーソン局在化 (物性物理学における相転移) を研究するのに役立ちます。
ちなみに、研究にある KAN のすべての例 (パラメーター スキャンを除く) は、単一の CPU で 10 分以内に再現できます。

KAN の出現は、機械学習の分野を常に支配してきた MLP アーキテクチャに直接挑戦し、ネットワーク全体に大騒動を引き起こしました。
機械学習の新しい時代が始まりました
機械学習の新しい時代が始まったという人もいます。

Google DeepMind の研究科学者は、「コルモゴロフ・アーノルドが再び攻撃する! あまり知られていない事実: この定理は、順列不変ニューラル ネットワーク (深さセット) に関する独創的な論文に登場し、この表現を示しています。アンサンブル/ GNN アグリゲーターは (特殊なケースとして) 構築されます。」

まったく新しいニューラル ネットワーク アーキテクチャが誕生しました。 KAN は、人工知能のトレーニングと微調整の方法を劇的に変えます。


AIは2.0時代に入ったということでしょうか?

一部のネチズンは、一般的な言葉を使って、KAN と MLP の違いを鮮やかに比喩しました:
コルモゴロフ・アーノルド・ネットワーク (KAN) は、どんなケーキも焼ける 3 次元ネットワークのようなものですレイヤー ケーキのレシピですが、多層パーセプトロン (MLP) はさまざまな層の数を備えたカスタム ケーキです。 MLP はより複雑ですがより一般的ですが、KAN は静的ですが、1 つのタスクではよりシンプルで高速です。

論文の著者であるMITのマックス・テグマーク教授は、最新の論文は、興味深い物理的および数学的問題を扱う場合、標準的なニューラルネットワークとは完全に異なるアーキテクチャがより少ないパラメータでより良い結果を達成できることを示していると述べた.高精度。

次に、ディープラーニングの未来を代表する KAN がどのように実装されているかを見てみましょう。
KAN がポーカー テーブルに戻ります
KAN の理論的基礎
コルモゴロフ – アーノルド表現定理 (コルモゴロフ – アーノルド表現定理) は、 f が有界領域の多変数連続関数で定義されている場合、この場合、関数は複数の一変数の加法連続関数の有限の組み合わせとして表現できます。

機械学習の場合、この問題は次のように説明できます。高次元関数を学習するプロセスは、多項式量の 1 次元関数を学習するように単純化できます。
しかし、これらの 1 次元関数は滑らかでないか、フラクタルでさえある可能性があり、実際には学習できない可能性があります。まさにこの「病理学的動作」のせいで、機械の分野におけるコルモゴロフ-アーノルド表現定理が機能します。つまり、理論は正しいが、実際には役に立たない。
この記事では、研究者らは機械学習の分野でのこの定理の応用について依然として楽観的であり、次の 2 つの改善点を提案しています。元の方程式には、非線形性と非線形性の 2 つの層しかありません。 1 つの隠れ層 (2n+1)。ネットワークを任意の幅と深さに一般化できます。アーノルドの代表。物理学者と数学者の違いと同様に、物理学者は典型的なシナリオに関心を持ち、数学者は最悪のシナリオに関心を持ちます。
KAN アーキテクチャ
コルモゴロフ-アーノルド ネットワーク (KAN) 設計の核となるアイデアは、多変数関数の近似問題を単一変数関数のセットの学習問題に変換することです。このフレームワーク内では、すべての一変量関数は、係数が学習可能な局所的な区分的多項式曲線である B スプラインを使用してパラメーター化できます。

元の定理の 2 層ネットワークをより深く、より広く拡張するために、研究者らは KAN の設計をサポートする定理のより「一般化された」バージョンを提案しました。 MLP のスタック構造 ネットワークの深さの改善に触発され、この記事では同様の概念である KAN 層も紹介しています。これは 1 次元の関数行列で構成され、各関数にはトレーニング可能なパラメーターがあります。
コルモゴロフ・アーノルドの定理によれば、元の KAN 層は、それぞれ異なる入力次元と出力次元に対応する内部関数と外部関数で構成され、KAN 層を積層するこの設計方法は、深さを拡張するだけでなく、深さも向上します。 KAN の解釈可能性と表現力を維持し、各層は単一変数関数で構成され、関数は独立して学習および理解できます。次の式の

fはKAN
実装の詳細

KANの設計コンセプトはシンプルで純粋にスタッキングに依存しているように見えますが、最適化するのは簡単ではありません、研究者もトレーニングの過程でいくつかのテクニックを学びました。
1. 残差活性化関数: 基底関数 b(x) とスプライン関数の組み合わせを導入し、残差接続の概念を使用して活性化関数 ϕ(x) を構築することで、トレーニングの安定性に貢献します。プロセス。
2. 初期化スケール (スケール): 活性化関数の初期化はゼロに近いスプライン関数に設定され、重み w は勾配の安定性を維持するのに役立つザビエル初期化方法を使用します。トレーニングの初期段階で。

3. スプライン グリッドを更新する: スプライン関数は制限された間隔で定義されており、ニューラル ネットワークのトレーニング プロセス中にアクティブ化値がこの間隔を超える可能性があるため、スプライン グリッドを動的に更新することで、スプライン関数が常に動作するようにすることができます。適切な範囲内で。
パラメータ
1. ネットワークの深さ: L
2. 各層の幅: N
3. 定義された G 間隔 (G+1 ネットワーク グリッド ポイント) に基づきます。 , k 次 (通常 k=3)
したがって、KAN のパラメータ量は約
比較として、MLP のパラメータ量は O(L*N^2) であり、こちらの方が優れていると思われますKAN よりも効率的ですが、KAN はより小さい層幅 (N) を使用できるため、汎化パフォーマンスが向上するだけでなく、解釈可能性も向上します。 
パフォーマンスの向上
妥当性チェックとして、研究者らは、200 ステップごとにネットワークを増やすことで、検証データセットとしてスムーズな KA (コルモゴロフ-アーノルド) 表現を持つことが知られている 5 つの例を構築しました KAN はグリッド方式でトレーニングされます、{3,5,10,20,50,100,200,500,1000} として G の範囲をカバーします
ベースライン モデルとして深さと幅が異なる MLP を使用し、KAN と MLP の両方で LBFGS アルゴリズムを使用します合計 1800 ステップを訓練し、比較のための指標としてRMSEを使用しました。
結果からわかるように、KAN の曲線はより不安定で、すぐに収束し、安定した状態に達することができ、特に高次元の状況では MLP のスケーリング曲線よりも優れています。 また、3 層 KAN のパフォーマンスが 2 層 KAN よりもはるかに強力であることもわかります。これは、期待どおり、より深い KAN がより強力な表現能力を備えていることを示しています。 研究者らは、ユーザーがKANとの対話中に最も解釈しやすい結果を得ることができることを示すために、単純な回帰実験を設計しました。 ユーザーが記号式を調べることに興味があると仮定すると、合計 5 つの対話型ステップが必要です。 ステップ 1: スパース化によるトレーニング。 完全に接続された KAN から開始して、スパース正則化を使用してトレーニングすると、ネットワークがスパースになるため、隠れ層の 5 つのニューロンのうち 4 つが効果がないように見えることがわかります。 ステップ 2: 枝刈り 自動枝刈りの後、不要な隠れニューロンをすべて破棄し、KAN を 1 つだけ残し、活性化関数を既知の符号関数と照合します。 ステップ 3: シンボリック関数を設定する ユーザーが KAN チャートを見つめてこれらのシンボリック式を正しく推測できると仮定すると、直接設定できます ユーザーがドメインの知識がない場合または、活性化関数がどのようなシンボリック関数であるかわからない場合、研究者はシンボリック候補を提案する関数 assign_symbolic を提供しています。 ステップ 4: さらなるトレーニング ネットワーク内のすべての活性化関数がシンボル化された後、残りのパラメーターはアフィン パラメーターのみになり、損失が機械精度 (機械精度) まで低下することが確認できたら、アフィン パラメーターのトレーニングを続けます。 、モデルが正しいシンボリック式を見つけたことがわかります。 ステップ 5: シンボリック式を出力する Sympy を使用して出力ノードのシンボリック式を計算し、正しい答えを確認します。 研究者らはまず、記号式に基づく KAN ネットワークの組み合わせ構造機能を実証するために、教師あり玩具データセット内の 6 つのサンプルを設計しました。 これにより、KAN が正しい単一変数関数を学習することに成功したことがわかり、視覚化によって KAN の思考プロセスを説明できます。 教師なし設定では、データセットには入力特徴 x のみが含まれます。特定の変数 (x1、x2、x3) 間の接続を設計することで、変数間の依存関係を見つける KAN モデルの機能をテストできます。 結果から判断すると、KAN モデルは変数間の関数依存性を見つけることに成功しましたが、実験はまだ合成データに対してのみ行われており、より体系的で制御可能な方法が必要であるとも著者は指摘しています。完全な関係を発見するために。 著者らは、特別な関数を当てはめることにより、モデルパラメータの数とRMSE損失が広がる平面内でKANとMLPのパレートフロンティアを示しています。 すべての特殊関数の中でも、KAN は常に MLP よりも優れたパレート フロントを持っています。 偏微分方程式を解くタスクにおいて、研究者らは、予測された解と真の解の間の L2 二乗損失と H1 二乗損失をプロットしました。 下の図では、最初の 2 つは損失のトレーニング ダイナミクスであり、3 番目と 4 番目は損失関数の数のサックリング則です。 以下の結果に示されているように、KAN は MLP と比較してより速く収束し、損失が少なく、より急峻な拡張則を持ちます。 壊滅的な忘却が機械学習における深刻な問題であることは誰もが知っています。 人工ニューラルネットワークと脳の違いは、脳には空間内で局所的に機能するさまざまなモジュールがあることです。新しいタスクを学習するとき、構造の再編成は関連するスキルを担当する局所領域でのみ発生し、他の領域は変化しません。 しかし、MLP を含むほとんどの人工ニューラル ネットワークにはこの局所性の概念がなく、これが壊滅的な忘却の原因である可能性があります。 研究により、KAN には局所的な可塑性があり、スプラインの局所性を使用して壊滅的な忘却を回避できることが証明されました。 考え方は非常に単純です。スプラインはローカルであるため、サンプルは近くの一部のスプライン係数にのみ影響し、遠くの係数は変化しません。 対照的に、MLP は通常、グローバル アクティベーション (ReLU/Tanh/SiLU など) を使用するため、ローカルな変更が制御不能に遠くの領域に伝播し、そこに保存されている情報が破壊される可能性があります。 研究者らは、1 次元回帰タスク (5 つのガウス ピークで構成される) を採用しました。各ピークの周囲のデータは、(一度にすべてではなく) KAN と MLP に順番に提示されます。 結果は以下の図に示されています。KANは現在のステージでデータが存在する領域のみを再構築し、以前の領域は変更しません。 そして、MLP は新しいデータサンプルを見た後に領域全体を再形成し、壊滅的な忘却につながります。 KANの誕生は将来の機械学習の応用にとって何を意味しますか? ノット理論は、低次元トポロジーの分野であり、3 多様体と 4 多様体のトポロジカル問題を明らかにし、生物学やトポロジカル量子コンピューティングなどの分野に幅広く応用されています。 2021 年、DeepMind チームは AI を使用して、Nature で初めてノット理論を証明しました。 論文アドレス: https://www.nature.com/articles/s41586-021-04086-x この研究では、教師あり学習と人間領域の専門家を通じて、代数的および幾何学的ノットの不変量。 つまり、勾配顕著性によって監視問題の主要な不変条件が特定され、これによりドメインの専門家が推測を提案し、その後洗練されて証明されました。 これに関して、著者は、KAN が同じ問題でノットの署名を予測するために良好な解釈可能な結果を達成できるかどうかを研究しています。 DeepMind の実験では、結び目理論データセットの研究の主な結果は次のとおりです: 1 ネットワーク帰属法を使用すると、署名 2 、署名を出力として扱います。 以下の表に示すように、KAN (G = 3, k = 3) には約 200 個のパラメーターがありますが、MLP には約 300,000 個のパラメーターがあります。
注目に値するのは、KAN はより正確であるだけではありません。同時に、パラメーターは MLP よりも効率的です。 解釈可能性の観点から、研究者らは各アクティベーションの透明度をそのサイズに基づいてスケールしたため、特徴の帰属がなくても、どの入力変数が重要であるかがすぐに明らかになりました。 その後、KAN は 3 つの重要な変数でトレーニングされ、78.2% のテスト精度を獲得しました。
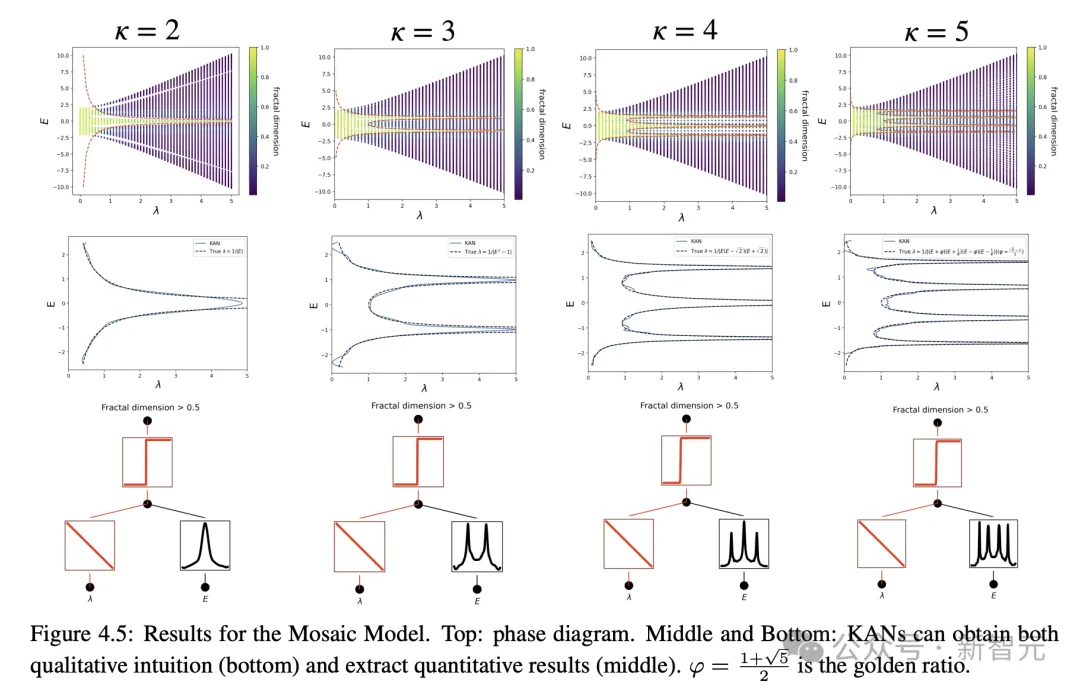
以下のように、著者は KAN を通じて、ノット データセット内の 3 つの数学的関係を再発見しました。 物理アンダーソンの位置特定が解決されました アンダーソンは、量子系の無秩序が電子の波動関数の局在化を引き起こし、その結果すべての伝送が停止するという基本的な現象です。 対照的に、三次元では、臨界エネルギーは、移動度エッジと呼ばれる、拡張状態と局在状態を分離する相境界を形成します。 これらの移動度エッジを理解することは、固体における金属絶縁体転移やフォトニックデバイスにおける光の局在効果などのさまざまな基本現象を説明するために重要です。 著者は調査を通じて、KAN を使用すると、数値的または記号的にモビリティ エッジを非常に簡単に抽出できることを発見しました。
明らかに、KAN は科学者にとって強力なアシスタントであり、重要な協力者となっています。 結局のところ、KAN は、精度、パラメータ効率、解釈可能性における利点のおかげで、AI+サイエンスにとって有用なモデル/ツールとなるでしょう。 将来的には、科学分野における KAN のさらなる応用はまだ検討されていません。 KANのインタラクティブな説明



解釈可能性の検証



パレート最適化

偏微分方程式を解く

継続的な学習により壊滅的な忘却は起こらない

ノット理論を発見し、その成果はDeepMindを超えました


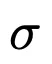 は主に中間距離
は主に中間距離  と縦方向距離 λ に依存することがわかります。
と縦方向距離 λ に依存することがわかります。  DeepMind のセットアップと同様に、署名 (偶数) はワンホット ベクトルとしてエンコードされ、ネットワークはクロスエントロピー損失でトレーニングされます。
DeepMind のセットアップと同様に、署名 (偶数) はワンホット ベクトルとしてエンコードされ、ネットワークはクロスエントロピー損失でトレーニングされます。  その結果、非常に小さな KAN は 81.6% のテスト精度を達成できるのに対し、DeepMind の 4 層幅 300MLP は 78% のテスト精度しか達成できないことがわかりました。
その結果、非常に小さな KAN は 81.6% のテスト精度を達成できるのに対し、DeepMind の 4 層幅 300MLP は 78% のテスト精度しか達成できないことがわかりました。 

 そして、物理アプリケーションでも、KAN は大きな役割を果たしました。
そして、物理アプリケーションでも、KAN は大きな役割を果たしました。 

以上がMLPは一夜にして消滅した! MIT カリフォルニア工科大学とその他の革新的な KAN が記録を破り、DeepMind を打ち砕く数学的定理を発見の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7663
7663
 15
15
 1393
1393
 52
52
 1205
1205
 24
24
 91
91
 11
11
 Web3トレーディングプラットフォームranking_web3グローバル交換トップ10の概要
Apr 21, 2025 am 10:45 AM
Web3トレーディングプラットフォームranking_web3グローバル交換トップ10の概要
Apr 21, 2025 am 10:45 AM
Binanceは、グローバルデジタルアセット取引エコシステムの大君主であり、その特性には次のものが含まれます。1。1日の平均取引量は1,500億ドルを超え、500の取引ペアをサポートし、主流の通貨の98%をカバーしています。 2。イノベーションマトリックスは、デリバティブ市場、Web3レイアウト、教育システムをカバーしています。 3.技術的な利点は、1秒あたり140万のトランザクションのピーク処理量を伴うミリ秒のマッチングエンジンです。 4.コンプライアンスの進捗状況は、15か国のライセンスを保持し、ヨーロッパと米国で準拠した事業体を確立します。
 トップ10の暗号通貨交換プラットフォーム世界最大のデジタル通貨交換リスト
Apr 21, 2025 pm 07:15 PM
トップ10の暗号通貨交換プラットフォーム世界最大のデジタル通貨交換リスト
Apr 21, 2025 pm 07:15 PM
交換は、今日の暗号通貨市場で重要な役割を果たしています。それらは、投資家が取引するためのプラットフォームであるだけでなく、市場の流動性と価格発見の重要なソースでもあります。世界最大の仮想通貨交換はトップ10にランクされており、これらの交換は取引量がはるかに先を行っているだけでなく、ユーザーエクスペリエンス、セキュリティ、革新的なサービスに独自の利点を持っています。リストの上にある交換は通常、ユーザーベースが大きく、広範な市場の影響力があり、その取引量と資産タイプは、他の取引所で到達するのが難しいことがよくあります。
 ETHアップグレード後の損失を避ける方法
Apr 21, 2025 am 10:03 AM
ETHアップグレード後の損失を避ける方法
Apr 21, 2025 am 10:03 AM
ETHアップグレード後、初心者は損失を避けるために次の戦略を採用する必要があります。1。宿題をして、ETHの基本的な知識とアップグレードコンテンツを理解する必要があります。 2。ポジションを制御し、水を少量でテストし、投資を多様化します。 3.取引計画を立て、目標を明確にし、停止ポイントを設定します。 4.合理的にプロファイルし、感情的な意思決定を避けます。 5。正式で信頼できる取引プラットフォームを選択します。 6.短期的な変動の影響を避けるために、長期的な保持を検討してください。
 通貨交換サークルのトップ10のプラットフォームは何ですか?
Apr 21, 2025 pm 12:21 PM
通貨交換サークルのトップ10のプラットフォームは何ですか?
Apr 21, 2025 pm 12:21 PM
上位の交換には、次のものが含まれます。1。世界最大の取引量であるバイナンスは600通貨をサポートし、スポット処理料は0.1%です。 2。バランスの取れたプラットフォームであるOKXは、708の取引ペアをサポートし、永続的な契約処理手数料は0.05%です。 3。Gate.io、2700の小通貨をカバーし、スポット処理料は0.1%-0.3%です。 4。Coinbase、米国のコンプライアンスベンチマーク、スポット処理料は0.5%です。 5。Kraken、トップセキュリティ、および定期的な予備監査。
 クロスチェーントランザクションとはどういう意味ですか?クロスチェーントランザクションとは何ですか?
Apr 21, 2025 pm 11:39 PM
クロスチェーントランザクションとはどういう意味ですか?クロスチェーントランザクションとは何ですか?
Apr 21, 2025 pm 11:39 PM
クロスチェーントランザクションをサポートする交換:1。Binance、2。Uniswap、3。Sushiswap、4。CurveFinance、5。Thorchain、6。1inchExchange、7。DLNTrade、これらのプラットフォームはさまざまな技術を通じてマルチチェーン資産トランザクションをサポートします。
 なぜ仮想通貨価格の上昇または下落があるのですか?なぜ仮想通貨価格の上昇または下落があるのですか?
Apr 21, 2025 am 08:57 AM
なぜ仮想通貨価格の上昇または下落があるのですか?なぜ仮想通貨価格の上昇または下落があるのですか?
Apr 21, 2025 am 08:57 AM
仮想通貨価格の上昇の要因には、次のものが含まれます。1。市場需要の増加、2。供給の減少、3。刺激された肯定的なニュース、4。楽観的な市場感情、5。マクロ経済環境。衰退要因は次のとおりです。1。市場需要の減少、2。供給の増加、3。ネガティブニュースのストライキ、4。悲観的市場感情、5。マクロ経済環境。
 WorldCoin(WLD)価格予測2025-2031:WLDは2031年までに4ドルに達しますか?
Apr 21, 2025 pm 02:42 PM
WorldCoin(WLD)価格予測2025-2031:WLDは2031年までに4ドルに達しますか?
Apr 21, 2025 pm 02:42 PM
WorldCoin(WLD)は、独自の生体認証とプライバシー保護メカニズムを備えた暗号通貨市場で際立っており、多くの投資家の注目を集めています。 WLDは、特にOpenai人工知能技術と組み合わせて、革新的なテクノロジーを備えたAltcoinsの間で驚くほど演奏しています。しかし、デジタル資産は今後数年間でどのように振る舞いますか? WLDの将来の価格を一緒に予測しましょう。 2025年のWLD価格予測は、2025年にWLDで大幅に増加すると予想されています。市場分析は、平均WLD価格が1.31ドルに達する可能性があり、最大1.36ドルであることを示しています。ただし、クマ市場では、価格は約0.55ドルに低下する可能性があります。この成長の期待は、主にWorldCoin2によるものです。
 通貨サークルでのレバレッジされた交換のランキングは
Apr 21, 2025 pm 11:24 PM
通貨サークルでのレバレッジされた交換のランキングは
Apr 21, 2025 pm 11:24 PM
2025年のレバレッジド取引、セキュリティ、ユーザーエクスペリエンスで優れたパフォーマンスを持つプラットフォームは次のとおりです。1。OKX、高周波トレーダーに適しており、最大100倍のレバレッジを提供します。 2。世界中の多通貨トレーダーに適したバイナンス、125倍の高いレバレッジを提供します。 3。Gate.io、プロのデリバティブプレーヤーに適し、100倍のレバレッジを提供します。 4。ビットゲットは、初心者やソーシャルトレーダーに適しており、最大100倍のレバレッジを提供します。 5。Kraken、安定した投資家に適しており、5倍のレバレッジを提供します。 6。Altcoinエクスプローラーに適したBybit。20倍のレバレッジを提供します。 7。低コストのトレーダーに適したKucoinは、10倍のレバレッジを提供します。 8。ビットフィネックス、シニアプレイに適しています




