爆発後の逆転? 「MLPを一夜で倒した」KAN:実は私もMLPです
完全接続フィードフォワード ニューラル ネットワークとしても知られる多層パーセプトロン (MLP) は、今日の深層学習モデルの基本的な構成要素です。 MLP は非線形関数を近似する機械学習のデフォルトの方法であるため、MLP の重要性はいくら強調してもしすぎることはありません。
しかし最近、MIT やその他の機関の研究者が、非常に有望な代替方法である KAN を提案しました。この方法は、精度と解釈可能性の点で MLP よりも優れています。さらに、非常に少数のパラメータで、はるかに多くのパラメータを使用して実行される MLP よりも優れたパフォーマンスを発揮できます。たとえば、著者らは、KAN を使用してノット理論の数学的法則を再発見し、より小規模なネットワークと高度な自動化で DeepMind の結果を再現したと述べています。具体的には、DeepMind の MLP には約 300,000 のパラメーターがありますが、KAN には約 200 のパラメーターしかありません。
微調整の内容は次のとおりです。 これらの驚くべき研究結果により、KAN は急速に人気を博し、多くの人々が KAN を研究するようになりました。すぐに、一部の人々がいくつかの疑問を提起しました。その中で、「KAN is just MLP」と題されたColabの文書が議論の焦点となった。
KANはただの普通のMLPですか?
上記のドキュメントの著者は、ReLU の前にいくつかの繰り返しとシフトを追加することで KAN を MLP として記述できると述べています。
短い例で、著者は KAN ネットワークを、同じ数のパラメータとわずかに非線形な構造を持つ通常の MLP に書き直す方法を示します。
覚えておく必要があるのは、KAN にはエッジに活性化関数があるということです。 B スプラインを使用します。示されている例では、簡単にするために、著者は区分線形関数のみを使用します。これによってネットワークのモデリング機能が変更されることはありません。
次は区分線形関数の例です:
def f(x):if x
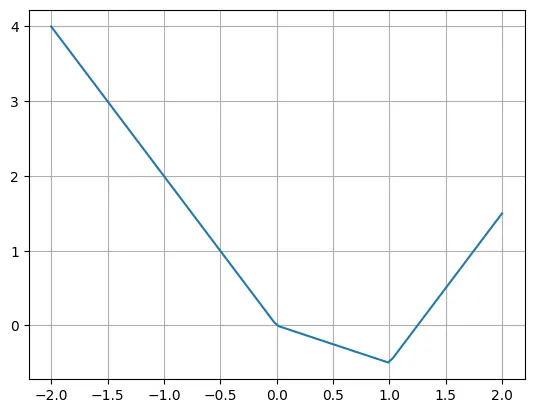
著者は、複数の ReLU と線形関数を使用してこの関数を簡単に書き直すことができると述べています。 ReLU の入力を移動する必要がある場合があることに注意してください。
plt.plot(X, -2*X + torch.relu(X)*1.5 + torch.relu(X-1)*2.5)plt.grid()
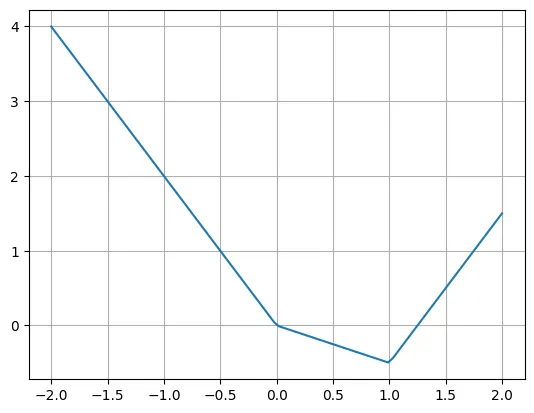
#本当の問題は、KAN 層を一般的な MLP 層に書き直す方法です。 n 個の入力ニューロン、m 個の出力ニューロンがあり、区分関数には k 個の部分があるとします。これには、n*m*k 個のパラメータが必要です (エッジごとに k 個のパラメータがあり、n*m 個のエッジがあります)。
次に、KAN エッジについて考えてみましょう。これを行うには、入力を k 回コピーし、各コピーを定数ずつシフトしてから、ReLU 層と線形層 (最初の層を除く) を実行する必要があります。グラフ的には次のようになります (C は定数、W は重みです):
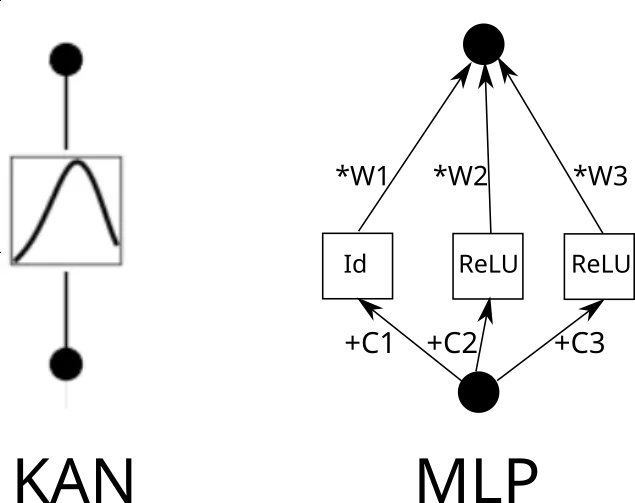
さて、各エッジに対してこのプロセスを繰り返すことができます。ただし、注意すべき点が 1 つあります。区分的線形関数グリッドがどこでも同じである場合、中間の ReLU 出力を共有し、その上で重みをブレンドするだけでよいということです。次のようになります:
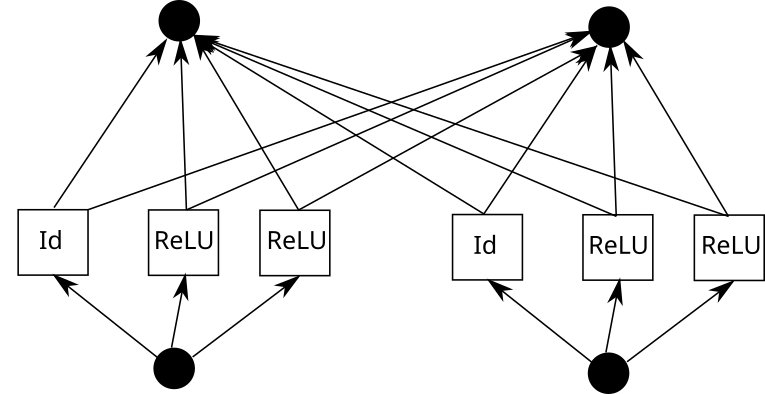
## Pytorch では、これは次のように変換されます:
k = 3 # Grid sizeinp_size = 5out_size = 7batch_size = 10X = torch.randn(batch_size, inp_size) # Our inputlinear = nn.Linear(inp_size*k, out_size)# Weightsrepeated = X.unsqueeze(1).repeat(1,k,1)shifts = torch.linspace(-1, 1, k).reshape(1,k,1)shifted = repeated + shiftsintermediate = torch.cat([shifted[:,:1,:], torch.relu(shifted[:,1:,:])], dim=1).flatten(1)outputs = linear(intermediate)
これで、レイヤーは次のようになります:
- Expand shift ReLU
- Linear
3 つの層を順番に検討します。
- シフト ReLU を展開します (ここから層 1 が始まります)
- Linear
- シフト ReLU の展開 (レイヤー 2 はここから始まります)
- Linear
- Expand shift ReLU (レイヤ 3 はここから始まります)
- Linear
入力拡張を無視し、再配置できます:
- リニア (レイヤー 1 はここから始まります)
- シフト ReLU の展開
- リニア (レイヤー 2 はここから始まります) )
- Expand shift ReLU
以下の層は基本的に MLP と呼ぶことができます。また、線形レイヤーを大きくし、拡張とシフトを削除して、(パラメーター コストは高くなりますが) モデリング機能を向上させることもできます。
- #リニア (レイヤー 2 はここから始まります)
- シフト展開 ReLU
##この例を通じて、著者は KAN が一種の MLP であることを示しています。この発言をきっかけに、誰もが 2 種類の方法について再考するようになりました。

KAN のアイデア、方法、結果の再検討
実際には、無視するだけでなく、 MLP KAN は清朝との関係をめぐって他の多くの政党からも疑問を呈されている。
要約すると、研究者らの議論は主に次の点に焦点を当てていました。
まず、KAN の主な貢献は、拡張速度や精度などではなく、解釈可能性にあります。
この論文の著者はかつて次のように述べました:
- KAN は MLP よりも速く拡張します。 KAN は、パラメータが少なくても MLP よりも精度が高くなります。
- KAN は直感的に視覚化できます。 KAN は、MLP では実現できない解釈可能性と対話性を提供します。 KAN を使用すると、新しい科学法則を発見できる可能性があります。
#その中でも、現実の問題を解決するためのモデルのネットワーク解釈可能性の重要性は自明です:

しかし、問題は次のとおりです。「彼らの主張は、学習が速く、解釈可能であるということだけであり、それ以外は何もありません。KAN のパラメーターが同等の NN よりもはるかに少ない場合、前者の方が意味があります。私はまだそう思っています。」 KAN のトレーニングは非常に不安定だと感じています。「
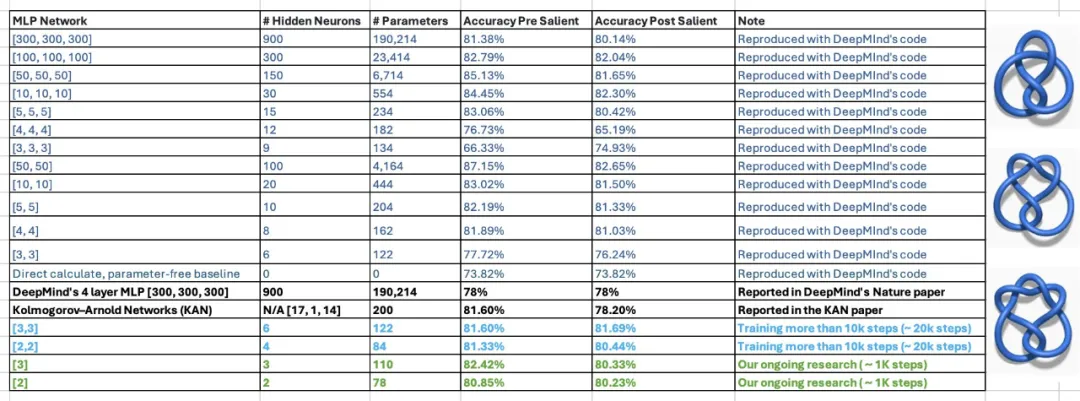
この声明にはまだ疑問があります。論文の中で、KAN の著者らは、KAN のわずか 200 パラメータを使用して、300,000 パラメータの MLP を使用した数学定理に関する DeepMind の研究を再現できたと述べています。この結果を見た後、ジョージア工科大学准教授ハンフリー・シーの学生 2 人が DeepMind の実験を再検査し、わずか 122 個のパラメータで DeepMind の MLP が KAN の 81.6% の精度に匹敵できることを発見しました。さらに、彼らは DeepMind コードに大きな変更を加えていません。この結果を達成するために、ネットワーク サイズを縮小し、ランダム シードを使用し、トレーニング時間を増やしただけです。

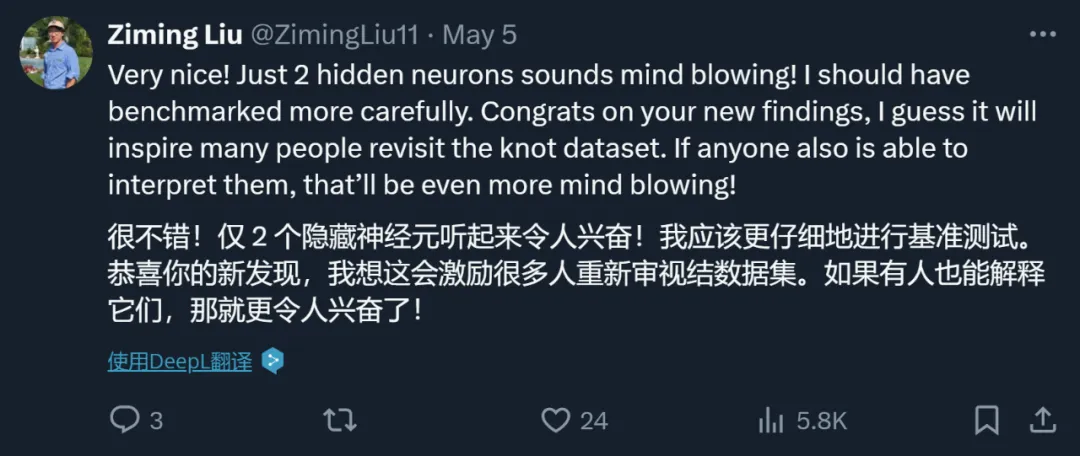
「はい、これは明らかに同じことです。KAN では最初にアクティベーションを行ってから線形結合を行いますが、MLP では最初に線形結合を行ってからアクティベーションを行います。私の知る限り、KAN を使用する主な理由は、この方法に疑問を投げかけることに加えて、合理性への回帰も求めています。この論文の評価: ##第三に、一部の研究者は、KAN のアイデアは新しいものではないと述べています。
「これは 1980 年代に研究されたものです。ハッカー ニュースのディスカッションで、この問題について議論しているイタリアの新聞が言及されていました。つまり、まったく新しいことではありません。40 年後になって、それは戻ってきたか、拒否されて再検討されているだけだ。」どちらかを発行します。 「これらのアイデアは新しいものではありませんが、作者がそれを忌避しているとは思えません。彼はすべてをうまくパッケージ化し、おもちゃデータの実験にいくつかの素晴らしい作業を加えただけです。しかし、これは貢献でもあります。」 ##同時に、Ian Goodfellow と Yoshua Bengio の論文 MaxOut (https://arxiv.org/pdf/ 1302.4389) についても言及されています。研究者の中には、この 2 つは「わずかに異なるものの、考え方はいくぶん似ている」と考えている人もいます。 著者: 当初の研究目標は確かに解釈可能性でした 白熱した議論の結果、著者の一人、サチン・ヴァイディア氏が来ました。フォワード。 この論文の執筆者の一人として、一言申し上げたいと思います。 KAN が受けている注目は驚くべきものであり、この議論はまさに新しいテクノロジーを限界まで押し上げ、何が機能し何が機能しないのかを明らかにするために必要なものです。 GitHub ホームページでは、論文著者の 1 人である Liu Ziming もこの研究の評価に回答しています: I最近よく聞かれる質問は、KAN が次世代 LLM になるかどうかというものです。これについては明確な判断ができません。 KAN は、高精度と解釈可能性を重視するアプリケーション向けに設計されています。私たちは LLM の解釈可能性を重視しますが、LLM と科学にとって解釈可能性は非常に異なる意味を持ちます。 LLM の高精度は重要ですか?スケーリングの法則はそのことを暗示しているように見えますが、おそらくあまり正確ではありません。さらに、精度は、LLM と科学にとって異なる意味を持つ場合もあります。 人々が KAN を批判することを歓迎します。実践こそが真実をテストする唯一の基準です。実際に試してみて、成功か失敗かが証明されるまでは分からないこともたくさんあります。私は KAN の成功を見たいと思っていますが、KAN の失敗にも同じくらい興味があります。 KAN と MLP は相互に代替できるものではありません。それぞれ、状況によっては利点があり、状況によっては制限があります。私は両方を包含する理論的枠組みに興味があり、もしかしたら新しい代替案を思いつくかもしれません(物理学者は統一理論が大好きです、申し訳ありません)。 KAN この論文の筆頭著者はLiu Ziming氏です。彼は物理学者および機械学習の研究者であり、現在は MIT と IAIFI で Max Tegmark のもとで博士課程の 3 年生です。彼の研究関心は、人工知能と物理学の交差点に焦点を当てています。 
 「人々は KAN 論文を深さとして扱うのをやめるべきだと思います。基本単位を学習し、単に解釈可能性に関する優れた論文として扱うという大きな変化です。」
「人々は KAN 論文を深さとして扱うのをやめるべきだと思います。基本単位を学習し、単に解釈可能性に関する優れた論文として扱うという大きな変化です。」 
モチベーションに関する背景を共有したいと思いました。 KAN を実装するための私たちの主なアイデアは、物理学者が自然法則について発見した洞察を「学習」できる、解釈可能な AI モデルの探索から生まれました。したがって、他の人も気づいているように、従来のブラックボックスモデルでは科学の基礎的な発見に重要な洞察を提供できないため、私たちはこの目標に完全に焦点を当てています。次に、物理学と数学に関連する例を通じて、KAN が解釈可能性の点で従来の方法よりも大幅に優れていることを示します。私たちは、KAN の有用性が当初の動機をはるかに超えて広がることを期待しています。
以上が爆発後の逆転? 「MLPを一夜で倒した」KAN:実は私もMLPですの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 Giteeページ静的なWebサイトの展開に失敗しました:単一のファイル404エラーをトラブルシューティングと解決する方法
Apr 04, 2025 pm 11:54 PM
Giteeページ静的なWebサイトの展開に失敗しました:単一のファイル404エラーをトラブルシューティングと解決する方法
Apr 04, 2025 pm 11:54 PM
GiteEpages静的Webサイトの展開が失敗しました:404エラーのトラブルシューティングと解像度Giteeを使用する
 WebアノテーションにY軸位置の適応レイアウトを実装する方法は?
Apr 04, 2025 pm 11:30 PM
WebアノテーションにY軸位置の適応レイアウトを実装する方法は?
Apr 04, 2025 pm 11:30 PM
Y軸位置Webアノテーション機能の適応アルゴリズムこの記事では、単語文書と同様の注釈関数、特に注釈間の間隔を扱う方法を実装する方法を探ります...
 c-subscript 3 subscript 5 c-subscript 3 subscript 5アルゴリズムチュートリアルを計算する方法
Apr 03, 2025 pm 10:33 PM
c-subscript 3 subscript 5 c-subscript 3 subscript 5アルゴリズムチュートリアルを計算する方法
Apr 03, 2025 pm 10:33 PM
C35の計算は、本質的に組み合わせ数学であり、5つの要素のうち3つから選択された組み合わせの数を表します。計算式はC53 = 5です! /(3! * 2!)。これは、ループで直接計算して効率を向上させ、オーバーフローを避けることができます。さらに、組み合わせの性質を理解し、効率的な計算方法をマスターすることは、確率統計、暗号化、アルゴリズム設計などの分野で多くの問題を解決するために重要です。
 要素UIの隣接する列の高さを自動的にコンテンツに自動的に適応させる方法は?
Apr 05, 2025 am 06:12 AM
要素UIの隣接する列の高さを自動的にコンテンツに自動的に適応させる方法は?
Apr 05, 2025 am 06:12 AM
同じ行の隣接する列の高さを自動的にコンテンツに自動的に適応させる方法は? Webデザインでは、この問題に遭遇することがよくあります。テーブルや列に多くの問題があるとき...
 GOプログラミングでは、MySQLとRedisの間で接続を正しく管理し、リソースをリリースする方法は?
Apr 02, 2025 pm 05:03 PM
GOプログラミングでは、MySQLとRedisの間で接続を正しく管理し、リソースをリリースする方法は?
Apr 02, 2025 pm 05:03 PM
GOプログラミングのリソース管理:MySQLとRedisは、特にデータベースとキャッシュを使用して、リソースを正しく管理する方法を学習するために接続およびリリースします...
 XMLをExcelに変換する方法
Apr 03, 2025 am 08:54 AM
XMLをExcelに変換する方法
Apr 03, 2025 am 08:54 AM
XMLをExcelに変換するには、組み込みのExcel機能またはサードパーティツールを使用する方法は2つあります。サードパーティツールには、XML To Excel Converter、XML2Excel、XML Candyが含まれます。
 H5ページの生産には継続的なメンテナンスが必要ですか?
Apr 05, 2025 pm 11:27 PM
H5ページの生産には継続的なメンテナンスが必要ですか?
Apr 05, 2025 pm 11:27 PM
H5ページは、コードの脆弱性、ブラウザー互換性、パフォーマンスの最適化、セキュリティの更新、ユーザーエクスペリエンスの改善などの要因のため、継続的に維持する必要があります。効果的なメンテナンス方法には、完全なテストシステムの確立、バージョン制御ツールの使用、定期的にページのパフォーマンスの監視、ユーザーフィードバックの収集、メンテナンス計画の策定が含まれます。
 個別の関数使用距離関数C使用チュートリアル
Apr 03, 2025 pm 10:27 PM
個別の関数使用距離関数C使用チュートリアル
Apr 03, 2025 pm 10:27 PM
std :: uniqueは、コンテナ内の隣接する複製要素を削除し、最後まで動かし、最初の複製要素を指すイテレーターを返します。 STD ::距離は、2つの反復器間の距離、つまり、指す要素の数を計算します。これらの2つの機能は、コードを最適化して効率を改善するのに役立ちますが、隣接する複製要素をstd ::のみ取引するというような、注意すべき落とし穴もあります。 STD ::非ランダムアクセスイテレーターを扱う場合、距離は効率が低くなります。これらの機能とベストプラクティスを習得することにより、これら2つの機能の力を完全に活用できます。






