時系列確率予測のための分位回帰
元の内容の意味を変えたり、内容を微調整したり、書き直したり、書き続けたりしないでください。 「分位回帰はこのニーズを満たし、定量化された確率で予測間隔を提供します。これは、特に応答変数の条件付き分布が重要な場合に、予測変数と応答変数の間の関係をモデル化するために使用される統計手法です。従来の回帰とは異なります」
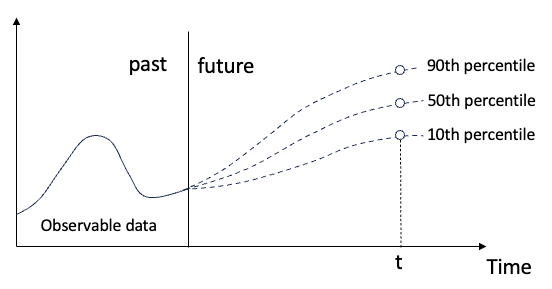 図 (A): 分位回帰
図 (A): 分位回帰
概念
分位回帰は、条件付き平均ではなく、応答変数の条件付きの大きさを推定することに焦点を当てています。一連の回帰変数 X と被説明変数 Y の分位数との間の線形関係。
既存の回帰モデルは、実際には被説明変数と説明変数の間の関係を研究する方法です。彼らは、説明変数と被説明変数の関係と、それらの誤差分布に焦点を当てています。中央値回帰と分位数回帰は、2 つの一般的な回帰モデルです。これらは、Koenker と Bassett (1978) に従って最初に提案されました。
通常の最小二乗回帰推定量の計算は、残差二乗和の最小化に基づいています。分位点回帰推定量の計算も、対称形式での絶対値残差の最小化に基づいています。このうち、中央値回帰演算は最小絶対偏差推定量 (LAD、最小絶対偏差推定量) です。
分位点回帰の利点
被説明変数の条件付き分布の全体像を説明します。被説明変数の条件付き期待値 (平均) を分析するだけでなく、説明変数が被説明変数の中央値と分位数にどのように影響するかも分析します。説明変数の数など異なる分位数での回帰係数推定値は異なることがよくあります。つまり、説明変数は異なる分位数に対して異なる影響を及ぼします。したがって、説明変数の異なる分位数の異なる効果は、被説明変数に対して異なる影響を及ぼします。
最小乗算法と比較して、中央値回帰の推定法は外れ値に対してより堅牢であり、分位回帰では誤差項について強い仮定を必要としないため、非正規状態の分布、中央値回帰係数量より健康的です。同時に、分位点回帰システムの量推定がより堅牢になります。
モンテカルロ シミュレーションに対する分位点回帰の利点は何ですか?まず、分位回帰では、予測子が与えられた場合に応答変数の条件付きの大きさを直接推定します。これは、モンテカルロ シミュレーションのように多数の可能な結果を生成するのではなく、応答変数の分布の特定の大きさの推定値を提供することを意味します。これは、五分位、四分位、極端な大きさなど、さまざまなレベルの予測の不確実性を理解するのに特に役立ちます。第 2 に、分位点回帰は、観測データを使用して変数間の関係を推定し、この関係に基づいて予測を行う、モデルベースの予測不確実性推定方法を提供します。対照的に、モンテカルロ シミュレーションは、入力変数の確率分布の指定と、ランダム サンプリングに基づいた結果の生成に依存します。
NeuralProphet は、(1) 分位点回帰と (2) 等角分位点回帰という 2 つの統計手法を提供します。等角分位数予測手法では、分位数回帰を行うためのキャリブレーション プロセスが追加されます。この記事では、Neural Prophet の分位回帰モジュールを使用して分位回帰予測を行います。このモジュールは、予測結果が観測データの分布と一致していることを確認するためのキャリブレーション プロセスを追加します。この章では、Neural Prophet の分位点回帰モジュールを使用します。
環境要件
NeuralProphet をインストールします。
!pip install neuralprophet!pip uninstall numpy!pip install git+https://github.com/ourownstory/neural_prophet.git numpy==1.23.5
必要なライブラリをインポートします。
%matplotlib inlinefrom matplotlib import pyplot as pltimport pandas as pdimport numpy as npimport loggingimport warningslogging.getLogger('prophet').setLevel(logging.ERROR)warnings.filterwarnings("ignore")データセット
共有自転車データ。このデータセットは、毎日のレンタル需要のほか、気温や風速などの他の気象フィールドを含む多変量データセットです。
data = pd.read_csv('/bike_sharing_daily.csv')data.tail() 写真(B): シェア自転車
写真(B): シェア自転車
シェア自転車の数をプロットします。 2 年目に需要が増加し、季節パターンに従っていることがわかります。
# convert string to datetime64data["ds"] = pd.to_datetime(data["dteday"])# create line plot of sales dataplt.plot(data['ds'], data["cnt"])plt.xlabel("date")plt.ylabel("Count")plt.show()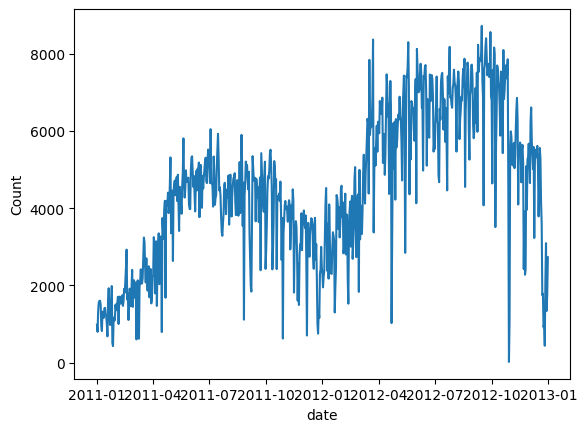 図(C): 一日のレンタル自転車需要
図(C): 一日のレンタル自転車需要
モデリングのための最も基本的なデータの準備をします。 NeuralProphet には、Prophet と同じ列名 ds および y が必要です。
构建分位数回归模型
直接在 NeuralProphet 中构建分位数回归。假设我们需要第 5、10、50、90 和 95 个量级的值。我们指定 quantile_list = [0.05,0.1,0.5,0.9,0.95],并打开参数 quantiles = quantile_list。
from neuralprophet import NeuralProphet, set_log_levelquantile_list=[0.05,0.1,0.5,0.9,0.95 ]# Model and predictionm = NeuralProphet(quantiles=quantile_list,yearly_seasnotallow=True,weekly_seasnotallow=True,daily_seasnotallow=False)m = m.add_country_holidays("US")m.set_plotting_backend("matplotlib")# Use matplotlibdf_train, df_test = m.split_df(df, valid_p=0.2)metrics = m.fit(df_train, validation_df=df_test, progress="bar")metrics.tail()分位数回归预测
我们将使用 .make_future_dataframe()为预测创建新数据帧,NeuralProphet 是基于 Prophet 的。参数 n_historic_predictions 为 100,只包含过去的 100 个数据点。如果设置为 True,则包括整个历史数据。我们设置 period=50 来预测未来 50 个数据点。
future = m.make_future_dataframe(df, periods=50, n_historic_predictinotallow=100) #, n_historic_predictinotallow=1)# Perform prediction with the trained modelsforecast = m.predict(df=future)forecast.tail(60)
预测结果存储在数据框架 predict 中。
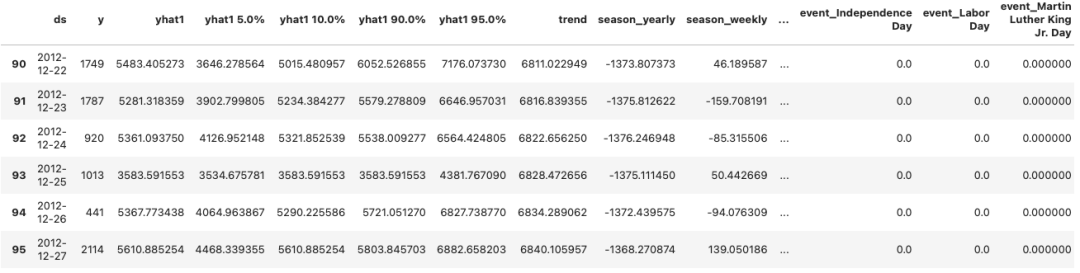 图 (D):预测
图 (D):预测
上述数据框架包含了绘制地图所需的所有数据元素。
m.plot(forecast, plotting_backend="plotly-static"#plotting_backend = "matplotlib")
预测区间是由分位数值提供的!
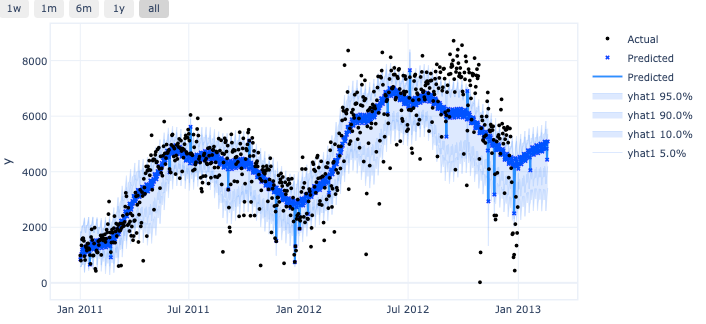 图 (E):分位数预测
图 (E):分位数预测
预测区间和置信区间的区别
预测区间和置信区间在流行趋势中很有帮助,因为它们可以量化不确定性。它们的目标、计算方法和应用是不同的。下面我将用回归来解释两者的区别。在图(F)中,我在左边画出了线性回归,在右边画出了分位数回归。
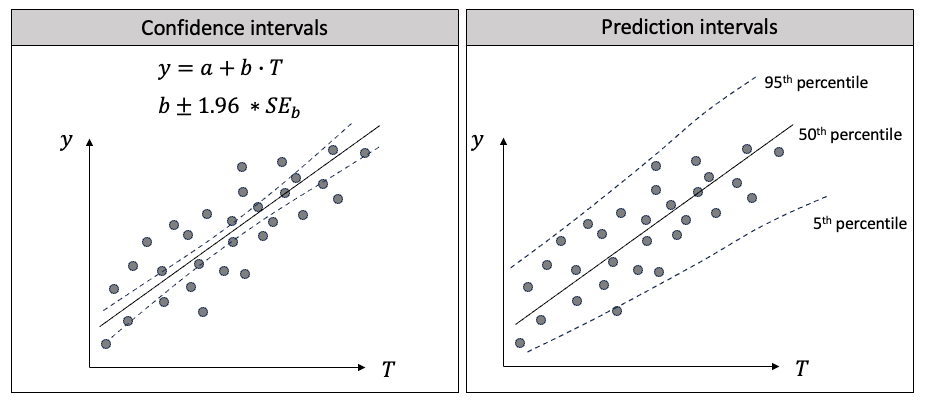 图(F):置信区间与预测区间的区别
图(F):置信区间与预测区间的区别
首先,它们的目标不同:
- 线性回归的主要目标是找到一条线,使预测值尽可能接近给定自变量值时因变量的条件均值。
- 分位数回归旨在提供未来观测值的范围,在一定的置信度下。它估计自变量与因变量条件分布的不同量化值之间的关系。
其次,它们的计算方法不同:
- 在线性回归中,置信区间是对自变量系数的区间估计,通常使用普通最小二乘法 (OLS) 找出数据点到直线的最小总距离。系数的变化会影响预测的条件均值 Y。
- 在分位数回归中,你可以选择依赖变量的不同量级来估计回归系数,通常是最小化绝对偏差的加权和,而不是使用OLS方法。
第三,它们的应用不同:
- 在线性回归中,预测的条件均值有 95% 的置信区间。置信区间较窄,因为它是条件平均值,而不是整个范围。
- 在分位数回归中,预测值有 95% 的概率落在预测区间的范围内。
写在最后
本文介绍了分位数回归预测区间的概念,以及如何利用 NeuralProphet 生成预测区间。我们还强调了预测区间和置信区间之间的差异,这在商业应用中经常引起混淆。后面将继续探讨另一项重要的技术,即复合分位数回归(CQR),用于预测不确定性。
以上が時系列確率予測のための分位回帰の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7517
7517
 15
15
 1378
1378
 52
52
 79
79
 11
11
 21
21
 66
66
 H5プロジェクトの実行方法
Apr 06, 2025 pm 12:21 PM
H5プロジェクトの実行方法
Apr 06, 2025 pm 12:21 PM
H5プロジェクトを実行するには、次の手順が必要です。Webサーバー、node.js、開発ツールなどの必要なツールのインストール。開発環境の構築、プロジェクトフォルダーの作成、プロジェクトの初期化、コードの書き込み。開発サーバーを起動し、コマンドラインを使用してコマンドを実行します。ブラウザでプロジェクトをプレビューし、開発サーバーURLを入力します。プロジェクトの公開、コードの最適化、プロジェクトの展開、Webサーバーの構成のセットアップ。
 H5ページの生産には継続的なメンテナンスが必要ですか?
Apr 05, 2025 pm 11:27 PM
H5ページの生産には継続的なメンテナンスが必要ですか?
Apr 05, 2025 pm 11:27 PM
H5ページは、コードの脆弱性、ブラウザー互換性、パフォーマンスの最適化、セキュリティの更新、ユーザーエクスペリエンスの改善などの要因のため、継続的に維持する必要があります。効果的なメンテナンス方法には、完全なテストシステムの確立、バージョン制御ツールの使用、定期的にページのパフォーマンスの監視、ユーザーフィードバックの収集、メンテナンス計画の策定が含まれます。
 自分でH5ページを作成する方法を学ぶことができますか?
Apr 06, 2025 am 06:36 AM
自分でH5ページを作成する方法を学ぶことができますか?
Apr 06, 2025 am 06:36 AM
自習H5ページの生産が可能ですが、迅速な成功ではありません。設計、フロントエンド開発、バックエンド相互作用ロジックを含むHTML、CSS、およびJavaScriptをマスターする必要があります。練習が鍵であり、チュートリアルを完成させ、資料のレビューを行い、オープンソースプロジェクトに参加することで学びます。パフォーマンスの最適化も重要であり、画像の最適化、HTTP要求の削減、適切なフレームワークの使用が必要です。自習への道は長く、継続的な学習とコミュニケーションが必要です。
 ブートストラップが変更された後の結果を表示する方法
Apr 07, 2025 am 10:03 AM
ブートストラップが変更された後の結果を表示する方法
Apr 07, 2025 am 10:03 AM
変更されたブートストラップの結果を表示する手順:ブラウザでHTMLファイルを直接開き、ブートストラップファイルが正しく参照されることを確認します。ブラウザキャッシュ(Ctrl Shift R)をクリアします。 CDNを使用する場合、開発者ツールでCSSを直接変更して、エフェクトをリアルタイムで表示できます。 Bootstrapソースコードを変更する場合は、ローカルファイルをダウンロードして交換するか、Webpackなどのビルドツールを使用してビルドコマンドを再実行します。
 Vue Paginationの使用方法
Apr 08, 2025 am 06:45 AM
Vue Paginationの使用方法
Apr 08, 2025 am 06:45 AM
ページネーションは、パフォーマンスとユーザーエクスペリエンスを向上させるために、大きなデータセットを小さなページに分割するテクノロジーです。 VUEでは、次の組み込みメソッドを使用してページを使用できます。ページの総数を計算します。TotalPages()トラバーサルページ番号:V-For Directive on Currentページを設定します。
 hadidb:pythonの軽量で水平方向にスケーラブルなデータベース
Apr 08, 2025 pm 06:12 PM
hadidb:pythonの軽量で水平方向にスケーラブルなデータベース
Apr 08, 2025 pm 06:12 PM
hadidb:軽量で高レベルのスケーラブルなPythonデータベースHadIDB(HadIDB)は、Pythonで記述された軽量データベースで、スケーラビリティが高くなっています。 PIPインストールを使用してHADIDBをインストールする:PIPINSTALLHADIDBユーザー管理CREATEユーザー:CREATEUSER()メソッド新しいユーザーを作成します。 Authentication()メソッドは、ユーザーのIDを認証します。 fromhadidb.operationimportuseruser_obj = user( "admin"、 "admin")user_obj。
 Prometheus MySQL ExporterでMySQLおよびMariadb液滴を監視します
Apr 08, 2025 pm 02:42 PM
Prometheus MySQL ExporterでMySQLおよびMariadb液滴を監視します
Apr 08, 2025 pm 02:42 PM
MySQLおよびMariaDBデータベースの効果的な監視は、最適なパフォーマンスを維持し、潜在的なボトルネックを特定し、システム全体の信頼性を確保するために重要です。 Prometheus MySQL Exporterは、プロアクティブな管理とトラブルシューティングに重要なデータベースメトリックに関する詳細な洞察を提供する強力なツールです。
 ブートストラップのJavaScriptの動作を表示する方法
Apr 07, 2025 am 10:33 AM
ブートストラップのJavaScriptの動作を表示する方法
Apr 07, 2025 am 10:33 AM
BootstrapのJavaScriptセクションは、静的なページに活力を与えるインタラクティブなコンポーネントを提供します。オープンソースコードを見ると、それがどのように機能するかを理解できます。イベントバインディングはDOMの操作とスタイルの変更をトリガーします。基本的な使用には、JavaScriptファイルの導入とAPIの使用が含まれ、高度な使用にはカスタムイベントと拡張機能が含まれます。よくある質問には、バージョンの競合やCSSスタイルの競合が含まれます。これは、コードをダブルチェックすることで解決できます。パフォーマンスの最適化のヒントには、オンデマンドの読み込みとコード圧縮が含まれます。 Bootstrap JavaScriptをマスターするための鍵は、その設計コンセプトを理解し、実用的なアプリケーションを組み合わせ、開発者ツールを使用してデバッグと探索することです。




