JavaScriptのデータ構造とアルゴリズムのバイナリツリーを詳しく解説_基礎知識
二分木の概念
バイナリ ツリーは、n (n>=0) 個のノードの有限集合です。この集合は、空のセット (空のバイナリ ツリー) であるか、ルート ノードと 2 つの相互に素なツリーで構成されます。ルート ノードの左側のサブツリーと右側のサブツリーで構成されます。

二分木の特徴
各ノードには最大 2 つのサブツリーがあるため、バイナリ ツリーには次数が 2 を超えるノードはありません。バイナリ ツリーの各ノードはオブジェクトであり、各データ ノードには 3 つのポインタがあります。これらのポインタは、親、左の子、右の子へのポインタです。各ノードはポインタを介して相互に接続されます。接続されたポインタ間の関係は親子関係です。
二分木ノードの定義
二分木のノードは次のように定義されます:
struct BinaryTreeNode
{
int m_nValue;
BinaryTreeNode* m_pLeft;
BinaryTreeNode* m_pRight;
};
二分木の 5 つの基本形式
空のバイナリツリー
ルートノードは 1 つだけです
ルートノードには左側のサブツリーのみがあります
ルートノードには正しいサブツリーのみがあります
ルートノードには左と右の両方のサブツリーがあります

3 つのノードを持つ通常のツリーには、2 層または 3 層の 2 つの状況しかありません。ただし、二分木は左右を区別する必要があるため、次の 5 つの形式に進化します。

特殊バイナリツリー
斜めの木
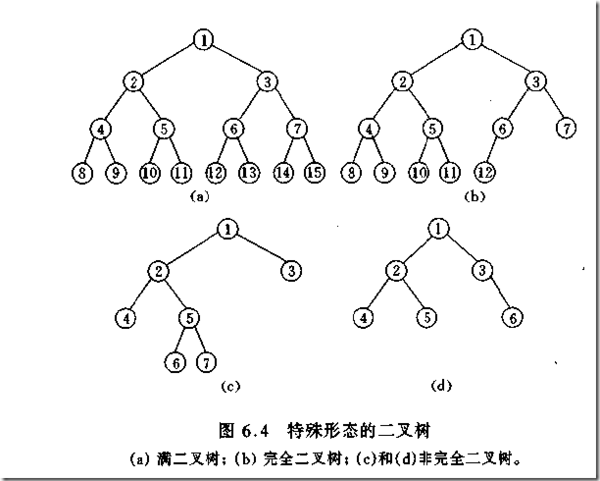
上の最後の写真の2枚目と3枚目にあるように。
完全なバイナリ ツリー
二分木で、すべての分岐ノードに左部分木と右部分木があり、すべての葉が同じレベルにある場合、そのような二分木は完全二分木と呼ばれます。以下に示すように:
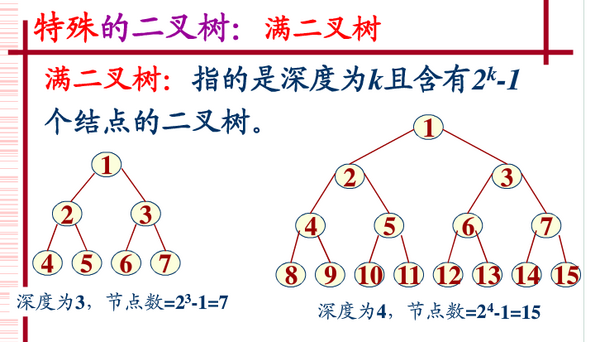
完全なバイナリツリー
完全なバイナリ ツリーとは、最後のレベルの左側がいっぱいで、右側がいっぱいかどうかにかかわらず、残りのレベルがいっぱいであることを意味します。深さが k でノード数が 2^k - 1 の二分木は、完全な二分木 (完全な二分木) です。深さ k で隙間のない木です。完全なバイナリツリーの特徴は次のとおりです:
リーフ ノードは、下の 2 つのレベルにのみ表示されます。
一番下の葉は左側の連続位置に集中する必要があります。
最後から 2 番目の層に葉ノードがある場合、それらは右側の連続した位置になければなりません。
ノードの次数が 1 の場合、ノードには子だけが残っています。
同じノード ツリーを持つバイナリ ツリー、完全なバイナリ ツリーの深さは最も浅くなります。
アルゴリズムは次のとおりです:
{
キューq; ツリー *ptr;
// 幅優先走査 (レベル走査) を実行し、NULL ノードをキューに入れます
q.push(ルート); While ((ptr = q.pop()) != NULL)
{
q.push(ptr->left);
q.push(ptr->right);
}
// 未訪問のノードがあるかどうかを判断します
(!q.is_empty()) {
ptr = q.pop();
// 未訪問の非 NULL ノードがある場合、ツリーには穴があり、不完全なバイナリ ツリーになります
If (NULL != ptr)
false を返す;
}
true を返します。
}
二分木のプロパティ
二分木のプロパティ 1: 二分木の i 番目のレベルには最大 2^(i-1) 個のノード (i>=1) があります
二分木の性質 2: 深さ k の二分木には最大 2^k-1 個のノード (k>=1) が含まれます
二分木の逐次記憶構造
バイナリ ツリーのシーケンシャル ストレージ構造では、1 次元配列を使用してバイナリ ツリー内の各ノードを格納し、ノードの格納場所はノード間の論理関係を反映できます。

バイナリリンクリスト
順次ストレージの適用性は強くないため、チェーンストレージ構造を考慮する必要があります。国際的な慣例によれば、バイナリ ツリーの保存には通常、チェーン ストレージ構造が使用されます。
バイナリ ツリーの各ノードには最大でも 2 つの子があるため、データ フィールドとそのための 2 つのポインタ フィールドを設計するのは自然な考え方です。このようなリンク リストをバイナリ リンク リストと呼びます。

バイナリツリートラバーサル
バイナリ ツリーのトラバースとは、ルート ノードから開始してバイナリ ツリー内のすべてのノードを特定の順序で訪問し、各ノードが 1 回だけ訪問されるようにすることを意味します。
バイナリ ツリーをトラバースするには、次の 3 つの方法があります。
(1) 事前順序トラバーサル (DLR)。最初にルート ノードにアクセスし、次に左のサブツリーをトラバースし、最後に右のサブツリーをトラバースします。ルート-左-右の略語。
(2) 順序トラバーサル (LDR)。最初に左側のサブツリーをトラバースし、次にルート ノードにアクセスし、最後に右側のサブツリーをトラバースします。左ルート右と略されます。
(3) ポストオーダートラバーサル (LRD)。最初に左側のサブツリーをトラバースし、次に右側のサブツリーをトラバースし、最後にルート ノードにアクセスします。左-右-ルートと略されます。
事前注文トラバーサル:
バイナリ ツリーが空の場合、操作は返されません。それ以外の場合は、ルート ノードが最初にアクセスされ、次に左のサブツリーが事前順序で走査され、次に右のサブツリーが事前順序で走査されます。
走査の順序は次のとおりです: A B D H I E J C F K G
// 事前注文トラバーサル
関数 preOrder(node){
If(!node == null){
putstr(node.show() " ");
preOrder(node.left);
preOrder(node.right);
}
}
順序トラバーサル:
ツリーが空の場合、操作は返されません。それ以外の場合は、ルート ノードから開始して (ルート ノードが最初に訪問されないことに注意してください)、ルート ノードの左側のサブツリーを順番にたどってから、ルート ノードにアクセスします。最後に、正しいサブツリーを順番にたどります。

走査の順序は次のとおりです: H D I B E J A F K C G
//再帰を使用して順序内トラバーサルを実装します
関数 inOrder(node){
If(!(node==null)){
inOrder(node.left);//最初に左側のサブツリーにアクセスします
putstr(node.show() " ");//ルートノードに再度アクセスします
inOrder(node.right);//右サブツリーへの最終アクセス
}
}
事後トラバーサル:
ツリーが空の場合は、何もしない操作が戻ります。それ以外の場合は、左右のサブツリーが左から右に、最初にリーフ、次にノードと走査され、最後にルート ノードが参照されます。

走査の順序は次のとおりです: H I D J E B K F G C A
//ポストオーダートラバーサル
関数 postOrder(node){
If(!node == null){
PostOrder(node.left);
postOrder(node.right);
putStr(node.show() " ");
}
}
二分探索木の実装
二分探索木 (BST) はノードで構成されているため、次のように Node ノード オブジェクトを定義します。
関数 Node(data,left,right){
This.data = データ;
This.left = left;// 左側のノードのリンクを保存します
This.right = right;
This.show = show;
}
関数 show(){
Return this.data;//ノードに保存されているデータを表示
}
最大値と最小値を求める
BST の最小値と最大値を見つけるのは、小さい値が常に左側の子ノードにあるため、非常に簡単です。BST の最小値を見つけるには、最後のノードが見つかるまで左側のサブツリーをたどるだけです。
最小値を求める
関数 getMin(){
var current = this.root;
While(!(current.left == null)){
現在 = current.left;
}
current.data を返します;
}
このメソッドは、BST の左端のノードに到達するまで、BST の左のサブツリーを 1 つずつ走査します。このノードは次のように定義されます。
最大値を求める
BST の最大値を見つけるには、最後のノードが見つかるまで右のサブツリーをたどるだけで済み、このノードに保存されている値が最大値になります。
var current = this.root;
While(!(current.right == null)){
current = current.right;
}
current.data を返します;
}

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7455
7455
 15
15
 1375
1375
 52
52
 77
77
 11
11
 14
14
 9
9
 C++ での機械学習アルゴリズムの実装: 一般的な課題と解決策
Jun 03, 2024 pm 01:25 PM
C++ での機械学習アルゴリズムの実装: 一般的な課題と解決策
Jun 03, 2024 pm 01:25 PM
C++ の機械学習アルゴリズムが直面する一般的な課題には、メモリ管理、マルチスレッド、パフォーマンスの最適化、保守性などがあります。解決策には、スマート ポインター、最新のスレッド ライブラリ、SIMD 命令、サードパーティ ライブラリの使用、コーディング スタイル ガイドラインの遵守、自動化ツールの使用が含まれます。実践的な事例では、Eigen ライブラリを使用して線形回帰アルゴリズムを実装し、メモリを効果的に管理し、高性能の行列演算を使用する方法を示します。
 C++sort 関数の基礎となる原則とアルゴリズムの選択を調べる
Apr 02, 2024 pm 05:36 PM
C++sort 関数の基礎となる原則とアルゴリズムの選択を調べる
Apr 02, 2024 pm 05:36 PM
C++sort 関数の最下層はマージ ソートを使用し、その複雑さは O(nlogn) で、クイック ソート、ヒープ ソート、安定したソートなど、さまざまなソート アルゴリズムの選択肢を提供します。
 Java 関数比較を使用して複雑なデータ構造を比較する
Apr 19, 2024 pm 10:24 PM
Java 関数比較を使用して複雑なデータ構造を比較する
Apr 19, 2024 pm 10:24 PM
Java で複雑なデータ構造を使用する場合、Comparator を使用して柔軟な比較メカニズムを提供します。具体的な手順には、コンパレータ クラスの定義、比較ロジックを定義するための比較メソッドの書き換えが含まれます。コンパレータインスタンスを作成します。 Collections.sort メソッドを使用して、コレクションとコンパレータのインスタンスを渡します。
 改良された検出アルゴリズム: 高解像度の光学式リモートセンシング画像でのターゲット検出用
Jun 06, 2024 pm 12:33 PM
改良された検出アルゴリズム: 高解像度の光学式リモートセンシング画像でのターゲット検出用
Jun 06, 2024 pm 12:33 PM
01 今後の概要 現時点では、検出効率と検出結果の適切なバランスを実現することが困難です。我々は、光学リモートセンシング画像におけるターゲット検出ネットワークの効果を向上させるために、多層特徴ピラミッド、マルチ検出ヘッド戦略、およびハイブリッドアテンションモジュールを使用して、高解像度光学リモートセンシング画像におけるターゲット検出のための強化されたYOLOv5アルゴリズムを開発しました。 SIMD データセットによると、新しいアルゴリズムの mAP は YOLOv5 より 2.2%、YOLOX より 8.48% 優れており、検出結果と速度のバランスがより優れています。 02 背景と動機 リモート センシング技術の急速な発展に伴い、航空機、自動車、建物など、地表上の多くの物体を記述するために高解像度の光学式リモート センシング画像が使用されています。リモートセンシング画像の判読における物体検出
 58 ポートレート プラットフォームの構築におけるアルゴリズムの適用
May 09, 2024 am 09:01 AM
58 ポートレート プラットフォームの構築におけるアルゴリズムの適用
May 09, 2024 am 09:01 AM
1. 58 Portraits プラットフォーム構築の背景 まず、58 Portraits プラットフォーム構築の背景についてお話ししたいと思います。 1. 従来のプロファイリング プラットフォームの従来の考え方ではもはや十分ではありません。ユーザー プロファイリング プラットフォームを構築するには、複数のビジネス分野からのデータを統合して、ユーザーの行動や関心を理解するためのデータ マイニングも必要です。最後に、ユーザー プロファイル データを効率的に保存、クエリ、共有し、プロファイル サービスを提供するためのデータ プラットフォーム機能も必要です。自社構築のビジネス プロファイリング プラットフォームとミドルオフィス プロファイリング プラットフォームの主な違いは、自社構築のプロファイリング プラットフォームは単一のビジネス ラインにサービスを提供し、オンデマンドでカスタマイズできることです。ミッドオフィス プラットフォームは複数のビジネス ラインにサービスを提供し、複雑な機能を備えていることです。モデリングを提供し、より一般的な機能を提供します。 2.58 中間プラットフォームのポートレート構築の背景のユーザーのポートレート 58
 Javaのデータ構造とアルゴリズム: 詳細な説明
May 08, 2024 pm 10:12 PM
Javaのデータ構造とアルゴリズム: 詳細な説明
May 08, 2024 pm 10:12 PM
データ構造とアルゴリズムは Java 開発の基礎です。この記事では、Java の主要なデータ構造 (配列、リンク リスト、ツリーなど) とアルゴリズム (並べ替え、検索、グラフ アルゴリズムなど) について詳しく説明します。これらの構造は、スコアを保存するための配列、買い物リストを管理するためのリンク リスト、再帰を実装するためのスタック、スレッドを同期するためのキュー、高速検索と認証のためのツリーとハッシュ テーブルの使用など、実際の例を通じて説明されています。これらの概念を理解すると、効率的で保守しやすい Java コードを作成できるようになります。
 PHP データ構造: AVL ツリーのバランス、効率的で秩序あるデータ構造の維持
Jun 03, 2024 am 09:58 AM
PHP データ構造: AVL ツリーのバランス、効率的で秩序あるデータ構造の維持
Jun 03, 2024 am 09:58 AM
AVL ツリーは、高速かつ効率的なデータ操作を保証するバランスのとれた二分探索ツリーです。バランスを達成するために、左回転と右回転の操作を実行し、バランスに反するサブツリーを調整します。 AVL ツリーは高さバランシングを利用して、ツリーの高さがノード数に対して常に小さくなるようにすることで、対数時間計算量 (O(logn)) の検索操作を実現し、大規模なデータ セットでもデータ構造の効率を維持します。
 画期的な CVM アルゴリズムが 40 年以上の計数の問題を解決します。コンピューター科学者がコインを投げて「ハムレット」を表す固有の単語を割り出す
Jun 07, 2024 pm 03:44 PM
画期的な CVM アルゴリズムが 40 年以上の計数の問題を解決します。コンピューター科学者がコインを投げて「ハムレット」を表す固有の単語を割り出す
Jun 07, 2024 pm 03:44 PM
数を数えるのは簡単そうに思えますが、実際にやってみるととても難しいです。あなたが野生動物の個体数調査を実施するために自然のままの熱帯雨林に運ばれたと想像してください。動物を見かけたら必ず写真を撮りましょう。デジタル カメラでは追跡された動物の総数のみが記録されますが、固有の動物の数に興味がありますが、統計はありません。では、このユニークな動物群にアクセスする最善の方法は何でしょうか?この時点で、今すぐ数え始めて、最後に写真から各新種をリストと比較すると言わなければなりません。ただし、この一般的なカウント方法は、数十億エントリに達する情報量には適さない場合があります。インド統計研究所、UNL、およびシンガポール国立大学のコンピューター科学者は、新しいアルゴリズムである CVM を提案しました。長いリスト内のさまざまな項目の計算を近似できます。




