合計 10000 件の関連コンテンツが見つかりました
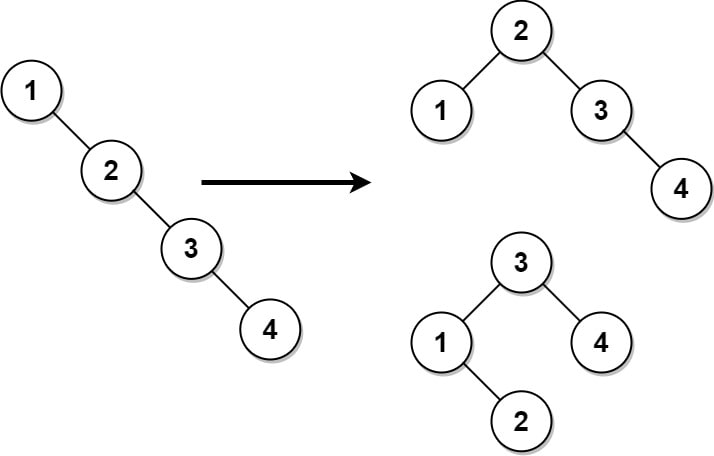
二分探索木のバランスを取る
記事の紹介:1382. 二分探索木のバランスを取る
中くらい
二分探索木のルートを指定すると、同じノード値を持つバランスの取れた二分探索木を返します。複数の回答がある場合は、いずれかを返します。
二分探索木は、深さが 0 の場合にバランスが取れています。
2024-07-16
コメント 0
549

Javaの二分探索木
記事の紹介:Java の二分探索ツリーのガイド。ここでは、Java での二分探索ツリーの定義、動作、コード例について説明します。
2024-08-30
コメント 0
295
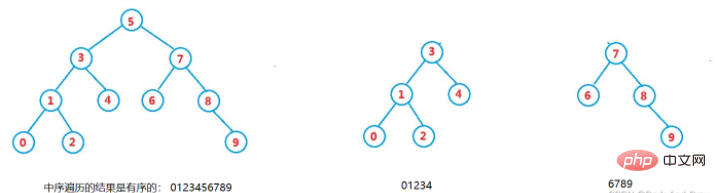
Javaバイナリサーチツリーの分析例
記事の紹介:概念 二分探索ツリーは二分ソート ツリーとも呼ばれ、空のツリー、または次のプロパティを持つ二分ツリーのいずれかです: 1. 左のサブツリーが空でない場合、左のサブツリー上のすべてのノードの値は Less です。ルートノードの値よりも大きくなります。 2. 右のサブツリーが空でない場合、右のサブツリー上のすべてのノードの値はルート ノードの値より大きくなります。 3. その左側と右側のサブツリーも、二分探索ツリーの実践のために直接準備されており、ツリー ノードのクラスと二分探索ツリーのクラスを定義します。二分木を検索する検索機能は、下図に示すような二分木を構築したことを前提としていますが、まず最初に考えなければならないのは、その二分木にある値があるかどうかをどうやって調べるかということです。上記のロジックでは、検索メソッド Complete を実行してみましょう。上記のロジックに従って、バイナリツリーを検索する挿入操作を書いてみましょう
2023-05-07
コメント 0
889
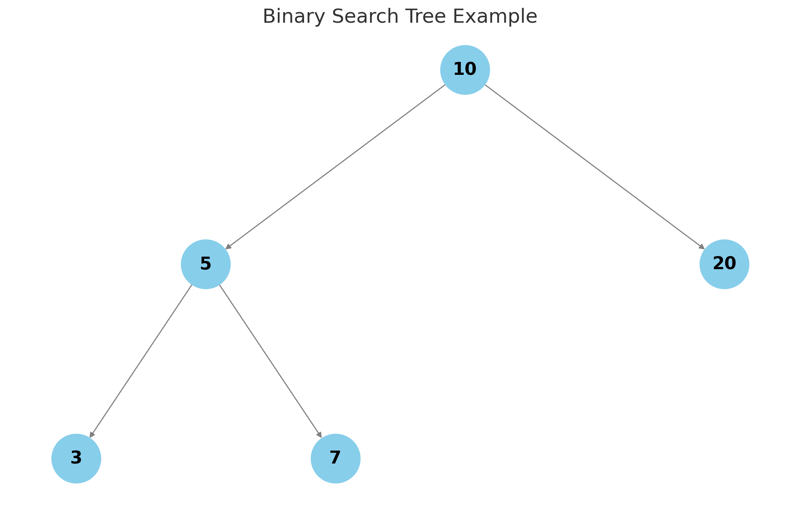
Javascriptの二分探索木
記事の紹介:JavaScript での二分探索ツリーの実装
この投稿では、JavaScript で基本的な二分探索ツリー (BST) を実装する方法を検討します。ノードの挿入と、さまざまなツリー走査方法 (in-order、pre-order、po) の実行について説明します。
2024-08-09
コメント 0
859

C++ のバイナリ ヒープとバイナリ検索ツリー
記事の紹介:C++ プログラミングでは、バイナリ ヒープとバイナリ検索ツリーはよく使用される 2 つのデータ構造であり、類似点もありますが、相違点もあります。この記事では、バイナリ ヒープとバイナリ サーチ ツリーの概念、基本操作、および応用シナリオをそれぞれ紹介します。 1. バイナリ ヒープ 1.1 概念 バイナリ ヒープは、次の 2 つの特性を満たす完全なバイナリ ツリーです。 1.1.1 ヒープの順序付け ヒープの順序付けとは、バイナリ ヒープ内で各ノードの値が次の値を超えない (または下回らない) ことを意味します。親ノードの値。ここでは例として最大ヒープを取り上げます。つまり、ルート ノードの値がツリー全体の最大値であり、
2023-08-22
コメント 0
1409

Javaを使用して二分探索木アルゴリズムを実装する方法
記事の紹介:Java を使用してバイナリ検索ツリー アルゴリズムを実装する方法 バイナリ検索ツリー (BinarySearchTree、略して BST) は、挿入、削除、検索などの操作を効率的に実装できる一般的に使用されるデータ構造です。この記事では、Java を使用して二分探索ツリーを実装する方法を紹介し、対応するコード例を示します。 1. 二分探索木の定義 二分探索木は、次の特徴を持つ順序付き木です。 各ノードは一意のキー値を持ちます。左側のサブツリーのキー値はノードのキー値より小さく、右側のサブツリーのキー値はノードのキー値より大きくなります。
2023-09-19
コメント 0
1123

JavaScript での二分探索ツリーの実装
記事の紹介:ツリー データ構造 ツリーは、いくつかのエッジで接続されたノードの集合です。慣例により、ツリーの各ノードは何らかのデータとその子ノードへの参照を保持します。二分探索木 二分探索木とは、値が小さいノードが左側に、値が小さいノードが左側に格納される二分木です。より高い値が右側に格納されます。たとえば、有効な BST の視覚的表現は -25/\ 20 36 /\ /\10223040 です。次に、JavaScript 言語で独自の二分探索ツリーを実装してみましょう。ステップ 1: ノード クラス このクラスは、BST 内のさまざまなポイントに存在する単一のノードを表します。 BSTは規制に従うだけです
2023-08-30
コメント 0
453

C# を使用して二分探索ツリー アルゴリズムを作成する方法
記事の紹介:C# を使用してバイナリ検索ツリー アルゴリズムを作成する方法には、特定のコード サンプルが必要です。バイナリ検索ツリー (BinarySearchTree、BST と呼ばれる) は、高速な挿入、検索、削除操作の特徴を持つ一般的に使用されるデータ構造です。 C# では、オブジェクト指向アプローチを使用して二分探索ツリー アルゴリズムを作成できます。まず、値と左右の子ノードへの 2 つのポインターを含む二分探索ツリー ノードのクラスを定義する必要があります。コードは次のようになります: publicclassBST
2023-09-19
コメント 0
1224

C++ でバイナリ ツリー内の最大の BST を変換する
記事の紹介:バイナリ ツリーでは、各子ノードには 2 つのノード (左と右) のみが含まれます。ツリー構造はデータを表現したものにすぎません。二分探索木 (BST) は、次の条件を満たす特別なタイプの二分木です。 - 左の子ノードは親に比べて小さい。 右の子ノードの親ノードは子ノードより大きい。 与えられた二分木があると仮定します。それらの中で最大のものは、二分探索ツリー (BST) です。このタスクでは、バイナリ ツリー内で最大の BST を見つける関数を作成します。二分木そのものがBSTである場合には、二分木全体のサイズを求めることができる。たとえば、「10 /\ 5 15 /\&nbs」と入力します。
2023-09-13
コメント 0
883
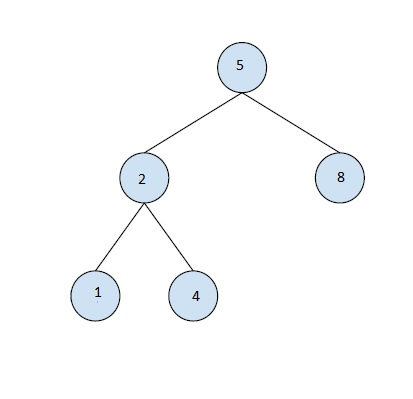
指定されたバイナリ ツリー内で最大のバイナリ検索サブツリーを見つける - C++ のエピソード 1
記事の紹介:この問題では、二分木 BT が与えられます。私たちのタスクは、指定されたバイナリ ツリー内で最大のバイナリ検索サブツリーを見つけることです。バイナリ ツリーは、データの保存に使用される特別なデータ構造です。バイナリ ツリーには、各ノードが最大 2 つの子ノードを持つことができるという特別な条件があります。二分探索木 (BST) は、左の部分木のキー値が親ノード (ルート ノード) のキー値より小さいという性質を満たす木です。右サブツリーのキー値は、その親ノード (ルート ノード) のキー値以上です。問題を理解するために、入力: 出力: 3 の例を見てみましょう 説明 FullbinarytreeisaBST. 解決策 この問題を解決する簡単な方法は、ツリーを順番に走査することです。ツリーの各ノードについて、そのサブツリーが二分探索であるかどうかを確認します。
2023-08-31
コメント 0
612

Java でゼロから作る二分探索木
記事の紹介:導入
二分探索ツリー (BST) は、各ノードが最大 2 つの子 (左の子と右の子と呼ばれます) を持つバイナリ ツリーの一種です。各ノードの左側のサブツリーには、そのノードの値よりも小さい値を持つノードのみが含まれます。
2024-07-17
コメント 0
866
バイナリ ツリーのリンク リスト
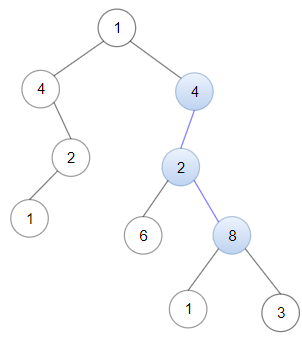
記事の紹介:1367. 二分木のリンクリスト
難易度: 中
トピック: リンク リスト、ツリー、深さ優先検索、幅優先検索、バイナリ ツリー
バイナリ ツリーのルートと、最初のノードとして head を持つリンク リストが与えられます。
li 内のすべての要素が一致する場合、True を返します。
2024-09-07
コメント 0
839
。等価な二分木を反転する
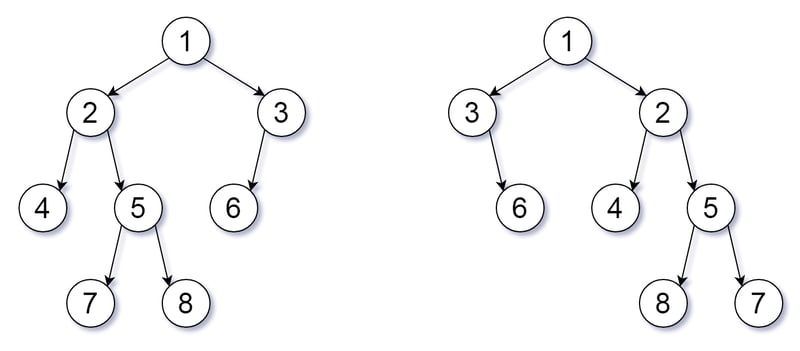
記事の紹介:951. 等価二分木を反転する
難易度: 中
トピック: ツリー、深さ優先検索、バイナリ ツリー
バイナリ ツリー T の場合、次のように反転操作を定義できます。任意のノードを選択し、左右の子サブツリーを交換します。
二分木 X は fli
2024-10-25
コメント 0
412
バイナリー ツリー II のいとこ
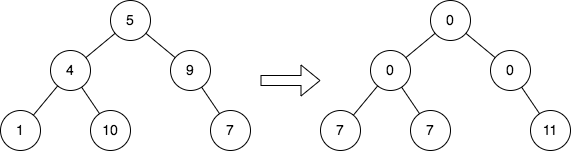
記事の紹介:2641. 二分木 II のいとこ
難易度: 中
トピック: ハッシュ テーブル、ツリー、深さ優先検索、幅優先検索、バイナリ ツリー
バイナリ ツリーのルートを指定すると、ツリー内の各ノードの値を、そのすべての従属ノードの値の合計で置き換えます。
2024-10-24
コメント 0
453

。バイナリ ツリー事後トラバーサル
記事の紹介:145. バイナリツリーポストオーダートラバーサル
難易度: 簡単
トピック: スタック、ツリー、深さ優先検索、バイナリ ツリー
バイナリ ツリーのルートを指定すると、そのノードの値の事後探索を返します。
例 1:
入力: root = [1,null,2,3]
出力: [
2024-08-26
コメント 0
559

サブツリー削除クエリ後のバイナリ ツリーの高さ
記事の紹介:2458. サブツリー削除クエリ後のバイナリ ツリーの高さ
難易度: ハード
トピック: 配列、ツリー、深さ優先検索、幅優先検索、バイナリ ツリー
n 個のノードを持つバイナリ ツリーのルートが与えられます。各ノードには 1 からの一意の値が割り当てられます。
2024-11-03
コメント 0
237

二分木における K 番目に大きい合計
記事の紹介:2583. 二分木における K 番目に大きい合計
難易度: 中
トピック: ツリー、幅優先検索、ソート、バイナリ ツリー
二分木のルートと正の整数 k が与えられます。
ツリー内のレベルの合計は、ノード t の値の合計です。
2024-10-23
コメント 0
529

二分木が二分探索木 (BST) であるかどうかをチェックする C 言語で書かれたプログラム
記事の紹介:バイナリ ツリーは、各ノードが 2 つの子ノードを持つツリー状のデータ構造です。これら 2 つの子ノードを左子ノードおよび右子ノードと呼びます。二分探索ツリー (BST) は、左側のサブツリーにルート ノードより小さい値を持つノードが含まれ、右側のサブツリーにルート ノードより大きい値を持つノードが含まれるツリー構造です。ここでは、二分木が BST であるかどうかを確認します。これを確認するには、二分木上の BST 条件を確認する必要があります。ルート ノードの場合、左側の子ノードの値はルート ノードの値より小さく、右側の子ノードの値はルート ノードの値より大きくなければなりません。この条件はすべてのノードで満たされる必要があります。ツリー内の子ノードと。バイナリツリーがBSTかどうかをチェックするプログラム#include<bits/stdc++.h>#in
2023-08-28
コメント 0
1205
Java でバイナリ ツリーの最も近い共通の祖先を見つける方法
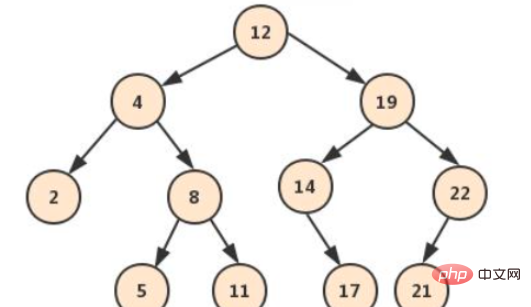
記事の紹介:アイデア 1: まず、この木が二分探索木であると仮定しましょう。まず、二分探索木とは何かを説明しましょう。二分探索木では、各ノードについて、その左側のサブツリーの値がその値よりも高くなります。小さい、右側のサブツリーの値は彼よりも大きくなります。したがって、二分探索ツリーの順序どおりの走査は、順序付けられたデータのセットです。上記のツリーでは、pq の最新の共通祖先が必要であると仮定します。通常の二分木では、次の状況のみが存在します: pq が左側にあり、pq が右側にあり、pq が左側にあり、1 つが右側にあり、pq の 1 つがルート ノードです。したがって、再帰的に左のサブツリーと右のサブツリーに移動して、pq ノードの共通の祖先を見つけます。見つかった場合はノードが返され、見つからなかった場合は空が返されます。上記の考えに基づいて、コード publicTr を簡単に書くことができます。
2023-05-01
コメント 0
1264

指定された二分探索ツリー内のすべてのより大きな値を各ノードに追加します
記事の紹介:BST または Binary Search Tree は、すべての左側のノードがルート ノードの値より小さい値を持ち、すべての右側のノードがルート ノードの値より大きい値を持つバイナリ ツリーの形式です。この問題では、バイナリ ツリーを取得し、現在のノード値より大きいすべての値をそれに追加します。 「より大きな値をすべて BST の各ノードに追加する」という問題は、BST の場合、現在のノード値よりも大きなすべてのノード値をそのノード値に追加するように単純化されます。 BST の各ノードにすべてのより大きな値のノードを追加する 問題ステートメント: 二分探索ツリー (BST) が与えられた場合、すべてのより大きな値のノードの合計を各ノードに追加する必要があります。 10 を入力してください /&nb
2023-09-07
コメント 0
1297



















