合計 10000 件の関連コンテンツが見つかりました
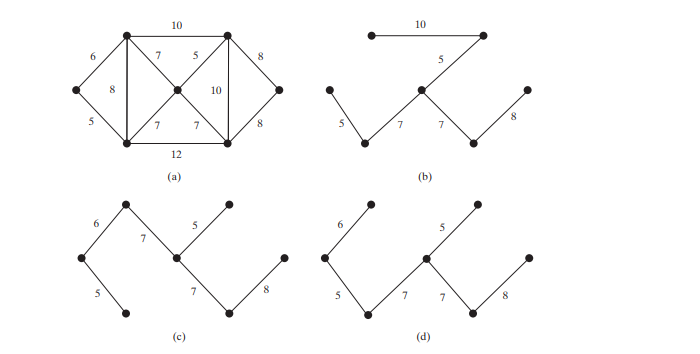
最小スパニングツリー
記事の紹介:グラフの最小スパニング ツリーは、最小の合計重みを持つスパニング ツリーです。
グラフには多数のスパニング ツリーが含まれる場合があります。エッジに重みが付けられているとします。最小スパニング ツリーには最小の合計重みがあります。たとえば、図の木々
2024-09-06
コメント 0
1192

C# を使用して最小スパニング ツリー アルゴリズムを作成する方法
記事の紹介:C# を使用して最小スパニング ツリー アルゴリズムを作成する方法. 最小スパニング ツリー アルゴリズムは、グラフの接続性の問題を解決するために使用される重要なグラフ理論アルゴリズムです。コンピューター サイエンスでは、最小スパニング ツリーとは、スパニング ツリーのすべてのエッジの重みの合計が最小となる、接続されたグラフのスパニング ツリーを指します。この記事では、C# を使用して最小限のスパニング ツリー アルゴリズムを作成する方法を紹介し、具体的なコード例を示します。まず、問題を表すグラフ データ構造を定義する必要があります。 C# では、隣接行列を使用してグラフを表現できます。隣接行列は、各要素が表す 2 次元配列です。
2023-09-19
コメント 0
731

Kruskal の最小スパニング ツリー アルゴリズム - C++ の貪欲なアルゴリズム
記事の紹介:スパニング ツリーは、すべての頂点を接続する有向無向グラフのサブグラフです。グラフ内には多数のスパニング ツリーが存在する場合があります。各グラフの最小スパニング ツリー (MST) の重みは、他のすべてのスパニング ツリーと同じかそれより小さくなります。重みはスパニング ツリーのエッジに割り当てられ、合計が各エッジに割り当てられた重みになります。 V はグラフ内の頂点の数であるため、V をエッジの数とすると、最小スパニング ツリーのエッジの数は (V-1) になります。クラスカルのアルゴリズムを使用して最小スパニング ツリーを見つけます。すべてのエッジは重みの降順以外に配置する必要があります。最小の辺を選択します。ループが形成されていない場合は、エッジが含まれます。ステップ 2 は、スパニング ツリーに (V-1) 個のエッジができるまで実行する必要があります。この場合、貪欲なアプローチを使用するように言われます。欲張りなオプションは、最小の重みを持つエッジを選択することです。例: このグラフの最小スパニング ツリーは (9-1)=8 です。
2023-08-28
コメント 0
1218

Javaを使用して最小スパニングツリーアルゴリズムを実装する方法
記事の紹介:Java を使用して最小スパニング ツリー アルゴリズムを実装する方法. 最小スパニング ツリー アルゴリズムは、重み付き接続グラフの最小スパニング ツリーを解くために使用されるグラフ理論の古典的な問題です。この記事では、Java 言語を使用してこのアルゴリズムを実装する方法を紹介し、具体的なコード例を示します。問題の説明 各エッジに重みがある接続グラフ G が与えられると、T 内のすべてのエッジの重みの合計が最小になるような最小スパニング ツリー T を見つける必要があります。 Prim のアルゴリズム Prim のアルゴリズムは、最小スパニング ツリー問題を解決するために使用される貪欲なアルゴリズムです。その基本的な考え方
2023-09-21
コメント 0
1108

C++ で最小スパニング ツリー アルゴリズムを使用する方法
記事の紹介:C++ で最小スパニング ツリー アルゴリズムを使用する方法。最小スパニング ツリー (MST) は、グラフ理論における重要な概念です。これは、無向接続グラフのすべての頂点を接続するエッジのサブセットを表し、これらのエッジの重みは と min です。プリムのアルゴリズムやクラスカルのアルゴリズムなど、最小スパニング ツリーを解くために使用できるアルゴリズムは数多くあります。この記事では、C++ を使用して Prim のアルゴリズムと Kruskal のアルゴリズムを実装する方法を紹介し、具体的なコード例を示します。プリムのアルゴリズムは、
2023-09-20
コメント 0
1269

Javaを使用してグラフの最小スパニングツリーアルゴリズムを実装する方法
記事の紹介:Java を使用してグラフの最小スパニング ツリー アルゴリズムの概念を実装する方法: 最小スパニング ツリー (MinimumSpanningTree、MST) とは、重み付き有向グラフまたは無向グラフで、グラフ内のすべての頂点と合計が含まれるツリーを見つけることを指します。重さは最小です。最小スパニング ツリー アルゴリズムは数多くありますが、最も古典的な 2 つのアルゴリズムは、Prim のアルゴリズムと Kruskal のアルゴリズムです。プリムのアルゴリズム: プリムのアルゴリズムは、頂点から開始して徐々に拡張するポイントベースの貪欲なアルゴリズムです。
2023-09-19
コメント 0
1279

最小スパニング ツリー用の C++ の Boruvka アルゴリズム
記事の紹介:グラフ理論では、接続された重み付きグラフの最小スパニング ツリー (MST) を見つけることが一般的な問題です。 MST は、すべての頂点を接続し、合計エッジの重みを最小化するグラフ エッジのサブセットです。この問題を解決する効率的なアルゴリズムが Boruvka アルゴリズムです。構文 structEdge{intsrc,dest,weight;};//union-findstructSubset{intparent,rank;};のサブセットを表す構造を定義します。 次に、Boruvka アルゴリズムで最小スパニング ツリーを見つける手順の概要を説明します。 MST を空のセットとして初期化します。 。頂点ごとに
2023-08-27
コメント 0
876

PHP で分割統治法を使用して最小スパニング ツリー問題を解決し、最適解を得るにはどうすればよいですか?
記事の紹介:PHP で分割統治法を使用して最小スパニング ツリー問題を解決し、最適解を得るにはどうすればよいですか?最小スパニング ツリーは、グラフ理論の古典的な問題です。接続されたグラフ内のすべての頂点のサブセットを見つけ、そのサブセットがツリーを形成し、すべてのエッジの重みの合計が最小になるようにエッジを接続することを目的としています。分割統治法とは、大きな問題を複数のサブ問題に分解し、そのサブ問題を 1 つずつ解決し、最後に結果を結合するという考え方です。分割統治法を使用して PHP の最小スパニング ツリー問題を解決するには、次の手順を実行します。グラフのデータ構造を定義します。
2023-09-19
コメント 0
919

PHP で最小スパニング ツリー問題の最適解を達成するために貪欲アルゴリズムを使用するにはどうすればよいですか?
記事の紹介:PHP で最小スパニング ツリー問題の最適解を達成するために貪欲アルゴリズムを使用する方法は?最小スパニング ツリー (MinimumSpanningTree) 問題は、接続された無向グラフ内で、このサブツリーにグラフ内のすべての頂点が含まれ、すべてのエッジの重みの合計が最小となるサブツリーを見つけることです。貪欲アルゴリズムは、この問題を解決するための一般的な手法の 1 つであり、毎回現在の最適解を選択することで、全体的な最適解を徐々に見つけます。まず、グラフの構造とエッジの重みを保存するグラフ クラスを定義する必要があります。以下はその例です
2023-09-19
コメント 0
1032

Prim と Kruskal の最小スパニング ツリー アルゴリズムが有向グラフで失敗するのはなぜですか?
記事の紹介:プリムの方法とクラスカルのアルゴリズムは、無向グラフで MST (最小スパニング ツリー) を見つけるための 2 つの一般的な方法です。ただし、これらの手法では、有向グラフの正しい MST を生成できません。これは、有向グラフがプリムとクラスカルのアルゴリズムで使用される基本的な仮定と手法に適合しないためです。プリムのアルゴリズム まず、プリムのアルゴリズムがあります。これは、すべての頂点がカバーされるまで貪欲に拡張する最小スパニング ツリーにエッジを追加することを含みます。 MST 内の頂点は、最小の重みを持つエッジを介して MST の外側の頂点に接続されます。無向グラフ内のすべてのエッジは任意の方向に移動できるため、MST から外部頂点までの最短パスを見つけるのは簡単です。ただし、有向グラフではエッジは常に一方向を向いており、直線が存在しない場合があります。
2023-09-02
コメント 0
665
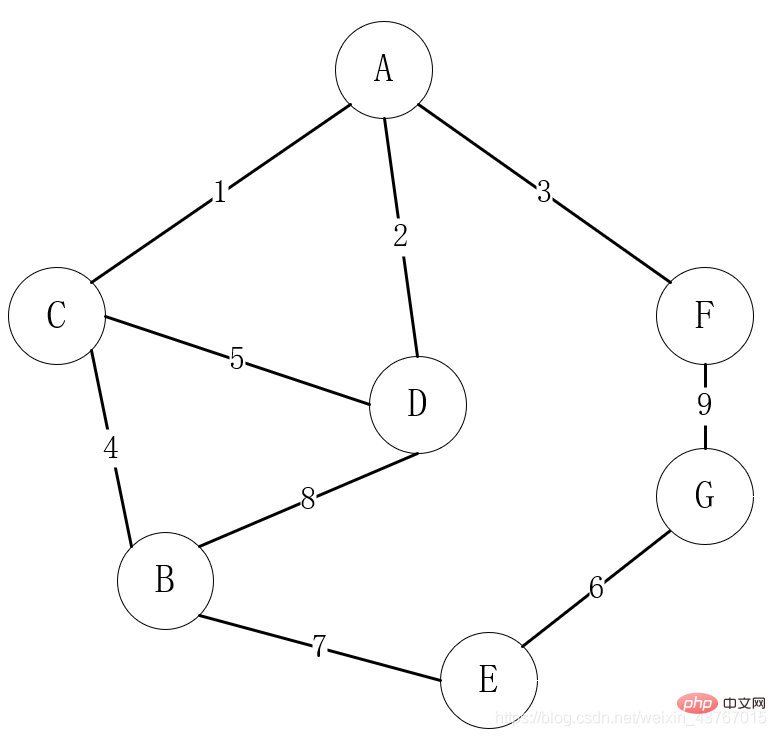
Javaで最小スパニングツリーを見つける方法
記事の紹介:1 最小スパニング ツリーの概要 スパニング ツリー (スパニング ツリー): 接続されたグラフのスパニング ツリーは、グラフ内の n 個の頂点すべてを含むが、ツリーを形成するのに十分な n-1 個のエッジのみを含む接続されたサブグラフを参照します。 n 個の頂点を持つスパニング ツリーには n-1 個のエッジしかありません。スパニング ツリーに別のエッジが追加されると、必ずサイクルが形成されます。最小スパニング ツリー (MinimumSpanningTree): 接続されたグラフ内のすべてのスパニング ツリーの中で、すべてのエッジの重みと最小のスパニング ツリーを最小スパニング ツリーと呼びます。生活の中で、グラフィック構造は最も広く使用されています。例えば、一般的な通信ネットワークの構築ルート選定では、村落を頂点とみなして、村落間に通信経路がある場合は、2点間のエッジや円弧としてカウントします。
2023-04-29
コメント 0
727

PHPの最小スパニングツリーアルゴリズムの詳細な説明
記事の紹介:PHP の最小スパニング ツリー アルゴリズムの詳細な説明 最小スパニング ツリー (略して MST) は、グラフ理論の重要な概念であり、接続されたグラフの最小重みエッジを選択する問題を解決するために使用されます。 PHP 言語では、いくつかの古典的な最小スパニング ツリー アルゴリズムを通じてこの関数を実装できます。この記事では、一般的に使用される 2 つの最小スパニング ツリー アルゴリズム、Prim のアルゴリズムと Kruskal のアルゴリズムを詳しく紹介し、対応する PHP コード例を示します。 1. プリムアルゴリズム プリムアルゴリズムとは、
2023-07-07
コメント 0
1302

最小全域ツリーの例の詳細な説明
記事の紹介:記事の転載元: 最小スパニングツリー - Prim アルゴリズムと Kruskal アルゴリズム
グラフのスパニング ツリーは、すべての頂点を含む非巡回接続サブグラフであり、重み付きグラフの最小スパニング ツリーは、最小の重みを持つスパニング ツリーです。
プリムのアルゴリズム
アルゴリズムの簡単な説明
1).入力: 頂点セットが V、エッジセットが E である重み付き接続グラフ。
2).初期化: Vnew = {x}、x は集合 V 内の任意のノード (開始点)、Enew = {} は空です。
3) 以下の操作を Vnew まで繰り返します。
2017-06-25
コメント 0
3467

ノード X から始まるサブツリーの最小重みと最大 D の距離を照会します。
記事の紹介:コンピューター プログラミングを行う場合、特定のノードから D 単位以上離れたノードをサブツリーに含めることができないという条件で、特定のノードに由来するサブツリーの最小重みを見つけることが必要になる場合があります。この問題は、グラフ理論、ツリーベースのアルゴリズム、ネットワーク最適化など、さまざまな分野やアプリケーションで発生します。サブツリーは、指定されたノードがサブツリーのルート ノードとして機能する、より大きなツリー構造のサブセットです。サブツリーには、ルート ノードのすべての子孫とそれらの接続エッジが含まれます。ノードの重みは、そのノードに割り当てられた特定の値を指し、その重要性、重要性、またはその他の関連するメトリックを表すことができます。この問題の目標は、ルート ノードから最大 D 単位離れたノードにサブツリーを制限しながら、サブツリー内のすべてのノード間の最小重みを見つけることです。次の記事では、サブツリーから最小重みをマイニングする複雑さについて詳しく説明します。
2023-08-25
コメント 0
1471

決定木の生成プロセスはid3アルゴリズムに関連しています
記事の紹介:ID3 アルゴリズムは、1986 年に Ross Quinlan によって提案された、デシジョン ツリーを生成するための古典的なアルゴリズムです。各フィーチャの情報ゲインを計算することにより、最適なフィーチャを分割ノードとして選択します。 ID3 アルゴリズムは機械学習やデータ マイニングの分野で広く使用されており、特に分類タスクで重要な役割を果たしています。これを使用すると、モデルの精度と解釈可能性が向上すると同時に、複数の特徴とカテゴリを持つ複雑なデータ セットを処理できるようになります。デシジョン ツリーは、分類または回帰に使用されるツリー構造です。ノードとエッジで構成され、ノードは特徴または属性を表し、エッジは可能な値または決定を表します。ルート ノードは最も重要な特徴を表し、リーフ ノードは最終的な分類結果を表します。決定木は、特徴量を段階的に判断して分類結果を決定します。
2024-01-22
コメント 0
1146
PHP树的深度编历生成迷宫及A*自动寻路算法实例分析
記事の紹介:PHP树的深度编历生成迷宫及A*自动寻路算法实例分析。PHP树的深度编历生成迷宫及A*自动寻路算法实例分析 这篇文章主要介绍了PHP树的深度编历生成迷宫及A*自动寻路算法,实例分析了php实现A*寻
2016-06-13
コメント 0
1082














