コース 中級  11343

コース紹介：「独習 IT ネットワーク Linux ロード バランシング ビデオ チュートリアル」では、主に nagin の下で Web、lvs、Linux 上でスクリプト操作を実行することで Linux ロード バランシングを実装します。

コース 上級  17647

コース紹介：「Shangxuetang MySQL ビデオチュートリアル」では、MySQL データベースのインストールから使用までのプロセスを紹介し、各リンクの具体的な操作を詳しく紹介します。

コース 上級  11354

コース紹介：「Brothers Band フロントエンド サンプル表示ビデオ チュートリアル」では、誰もが HTML5 と CSS3 を使いこなせるように、HTML5 と CSS3 テクノロジーのサンプルを紹介します。

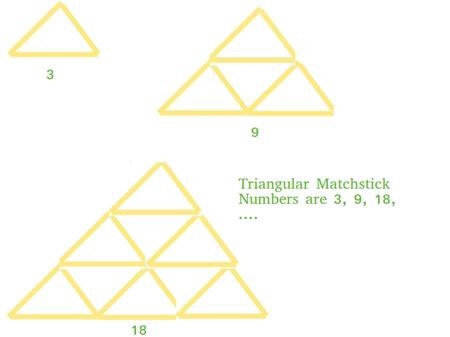
コース紹介：マッチ棒を正三角形になるように並べた三角形を三角マッチ数といいます。三角形の一致の数は、三角形の一致を形成するために必要な一致の数です。この問題では、数値は一致ピラミッドの底 X です。私たちのタスクは、x レベルのマッチのピラミッドを形成するために必要なマッチ棒の合計数を出力するプログラムを作成することです。概念を明確にするために例を見てみましょう。入力:7出力:84 は、これが三角関数の拡張であることを説明しています。整数 X の場合、必要なマッチ棒は、三角形の数の 3 倍になります。

2023-09-23 コメント 0  1410

コース紹介：この記事では、C++ で直角三角形を形成する斜辺と面積の可能な組み合わせの数を求める方法を説明します。直角三角形を形成する斜辺と面積 (H,A) のすべての可能なペアの数を決定する必要があります。ここで、H は斜辺、A は面積です。この例では、x = 直角三角形の底辺 y = 直角三角形の高さ H = 直角三角形の斜辺 直角三角形の面積 A=(x*y)/2 または 4*A2=(x*y ) 2…(1)また、x2+y2=H2 であることもわかっています…(2)(1)&(2)を解く4*A2=x2(H2-x2)x2 の二次方程式を解き、D( 判別式)>

2023-09-08 コメント 0  1110

コース紹介：グラフ内で三角形を形成するために必要な辺の最小数を決定するために、中心間のネットワークを分析しました。三角形は、3 つのハブが排他的に関連付けられている場合、またはエッジによって迂回して関連付けられている場合に形成できます。必要なエッジの最小数は、3 つのハブ間の既存の接続で失われるエッジの数と同じです。グラフを見て無関係な中心を区別することで、三角形を形成するために必要な追加の辺の数を計算できます。この方法は、グラフの中心間に三角形の関係を作成するために最小限の調整が必要なため、異なります。使用されるメソッド グラフ トラバーサル メソッド 三角形を作成するために必要な辺の最小数を見つけるために使用されるグラフ トラバーサル メソッドには、深さ優先検索 (DFS) や幅優先検索 (BFS) などのトラバーサル計算を使用してグラフを調べることが含まれます。各チャートから

2023-08-25 コメント 0  939

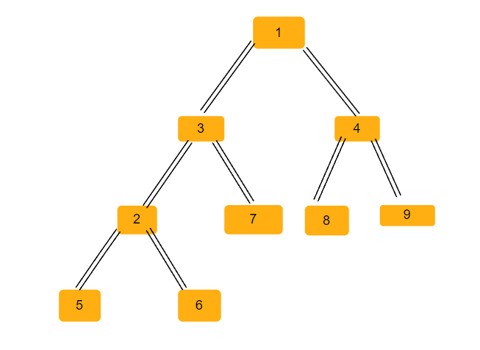
コース紹介：バイナリ ツリーは、各ノードが最大 2 つの子ノードを持つことができるデータ構造です。これらの子は、それぞれ左の子と右の子と呼ばれます。親の配列表現が与えられたとします。それを使用してバイナリ ツリーを作成する必要があります。二分木には複数の二等辺三角形が含まれる場合があります。この二分木で可能な二等辺三角形の総数を見つけなければなりません。この記事では、C++ でこの問題を解決するためのいくつかの手法を検討します。問題を理解すると、親配列が得られます。配列インデックスがツリー ノードの値を形成し、配列内の値がその特定のインデックスの親ノードを与えるように、それをバイナリ ツリーの形式で表す必要があります。 -1 は常にルートの親であることに注意してください。以下に、配列とそのバイナリ ツリー表現を示します。親配列=[0,-1,3,1,

2023-09-05 コメント 0  1104

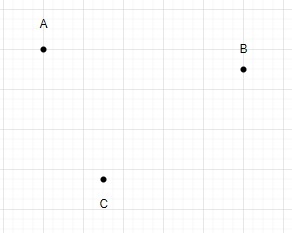
コース紹介：n 個の点が与えられた平面上の三角形の数を数え、同一線上にある点の数を 2 つ以下に制限する方法を見てみましょう。同一直線上にある点が 2 つ以下である平面内の三角形の数を数えるのは、コンピュータ グラフィックス、画像処理、その他のコンピュータ サイエンスの分野に応用される計算幾何学の典型的な問題です。たとえば、3D グラフィックスの 3D シーンから 2D 画像を作成する場合、共線点が 2 つ以下の平面内の三角形を計算するという問題が発生することがあります。この場合、三角形カウント プロセスを使用して、3D シーンを平面に投影した後の最終的な 2D 画像にいくつの三角形が存在するかを判断できます。これにより、シーンの複雑さを判断し、レンダリング速度を向上させることができます。画像処理では、画像内の固有のオブジェクトや形状の数を数えたい場合がありますが、この問題は非常に重要です。

2023-09-05 コメント 0  1286