碰到了一个关于元组的算法问题
请大家帮忙看看,能不能给个答案,或者解决思路也行.
谢谢!
三元组(a,b,c)标识a币种到b币种的汇率为c，反向亦成立。 输入一堆这样的三元组，再指定两个币种x y，问x->y的汇率是多少？ 请编程实现，并给出时间、空间复杂度。 注意：x->y的汇率是唯一的。
光阴似箭催人老，日月如移越少年。
アイデア: トリプレット -> 有向グラフ -> 行列乗算またはフロイド・ウォーシャル。
たとえば、取得される外国為替価格は次のとおりです:
最初の行は、1 元ごとに 0.116 ポンドに交換できることを示しています。各トリプル (c1, c2, r) は、次の 2 つの重み付きエッジに対応します。 /コード>。これらの引用符は実際に有向グラフを与えます: (c1, c2, r)对应两条带权重的边：c1 -> c2 weighted r和c2 -> c1 weighted 1/r。这些牌价实际上给出一个有向图：
(c1, c2, r)
c1 -> c2 weighted r
c2 -> c1 weighted 1/r
这里假设给出的三元组不会导出矛盾，且有向图是联通的（不会有折算不到的情况）。这个有向图写成带权重的邻接矩阵就是：
矩阵元素A[i,j]表示1单位i币种可以兑换多少单位的j币种。矩阵中的零代表目前汇率未知。
A[i,j]
i
j
把矩阵A连乘可以逐步去除这些零元素。但是要把普通矩阵相乘中计算点积的加法替换成“取第一个大于零的数，若没有则为零”的操作。例如：(1,2,3).(0,3,2) = first_positive(1*0, 2*3, 3*2) = 6。
A
(1,2,3).(0,3,2) = first_positive(1*0, 2*3, 3*2) = 6
用“汇率乘法”计算A的乘方，A^k表示最多经过k-1步折算得到的汇率表，一直算到A^k中没有零停止。如果有n种货币，最多计算到A^(n-1)。
A^k
k-1
n
A^(n-1)
A^3：
A^3
观察A^3的第一行，它是所有货币对人民币的比价。任两种货币的比价就是把它们对人民币的比价的商。所以其实一开始用A的第一行参加计算就好：A[1] * A * ... * A (最多n-1次)
A[1] * A * ... * A (最多n-1次)
ここでは、与えられたトリプレットは矛盾を生じず、有向グラフはつながっている（変換漏れはない）と仮定します。この有向グラフは、重み付き隣接行列として記述されます。
A[1] * A * ... * A (n-1 回まで)
トリプルの配列が提供された場合、x->y 為替レートを計算するための最適解を生成します: 有向グラフ最短経路アルゴリズム
毎回異なるトリプル配列を指定した場合、取得する必要がある結果は 1 つだけです: 有向グラフ経路探索アルゴリズム
タプルは辞書のキーとして使用できます
上記のアルゴリズムの一部は作成が非常に複雑です。簡単なアルゴリズムを書いてみましょう。 リーリー
リーリー
![[Web フロントエンド] Node.js クイック スタート](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
アイデア: トリプレット -> 有向グラフ -> 行列乗算またはフロイド・ウォーシャル。
たとえば、取得される外国為替価格は次のとおりです:
最初の行は、1 元ごとに 0.116 ポンドに交換できることを示しています。各トリプル
(c1, c2, r)は、次の 2 つの重み付きエッジに対応します。 /コード>。これらの引用符は実際に有向グラフを与えます:(c1, c2, r)对应两条带权重的边：c1 -> c2 weighted r和c2 -> c1 weighted 1/r。这些牌价实际上给出一个有向图：这里假设给出的三元组不会导出矛盾，且有向图是联通的（不会有折算不到的情况）。这个有向图写成带权重的邻接矩阵就是：
矩阵元素
A[i,j]表示1单位i币种可以兑换多少单位的j币种。矩阵中的零代表目前汇率未知。矩阵乘法
把矩阵
A连乘可以逐步去除这些零元素。但是要把普通矩阵相乘中计算点积的加法替换成“取第一个大于零的数，若没有则为零”的操作。例如：(1,2,3).(0,3,2) = first_positive(1*0, 2*3, 3*2) = 6。用“汇率乘法”计算
A的乘方，A^k表示最多经过k-1步折算得到的汇率表，一直算到A^k中没有零停止。如果有n种货币，最多计算到A^(n-1)。A^3：观察
A^3的第一行，它是所有货币对人民币的比价。任两种货币的比价就是把它们对人民币的比价的商。所以其实一开始用A的第一行参加计算就好：A[1] * A * ... * A (最多n-1次)ここでは、与えられたトリプレットは矛盾を生じず、有向グラフはつながっている（変換漏れはない）と仮定します。この有向グラフは、重み付き隣接行列として記述されます。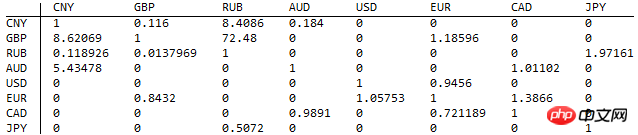
行列要素A[i,j]は、i通貨 1 単位と交換できるj通貨単位の数を表します。マトリックスのゼロは、現在の為替レートが不明であることを表します。 🎜 🎜行列の乗算🎜 🎜行列Aを乗算すると、これらのゼロ要素を徐々に削除できます。ただし、通常の行列の乗算における内積の計算の追加は、「ゼロより大きい最初の数値を取得するか、そうでない場合はゼロを取得する」という操作に置き換える必要があります。例:(1,2,3).(0,3,2) = first_positive(1*0, 2*3, 3*2) = 6。 🎜 🎜「為替レート乗算」を使用してAの累乗を計算します。A^kは最大k-1ステップで変換された為替レート テーブルを表します、常にA^kにゼロがなくなるまでカウントが停止します。n通貨がある場合、最大計算はA^(n-1)です。 🎜 🎜A^3:🎜
A^3の最初の行に注目してください。これは、人民元に対するすべての通貨の価格比較です。 2 つの通貨の比較は、人民元との比較の商となります。したがって、実際には、Aの最初の行を使用して計算に参加するだけです:A[1] * A * ... * A (n-1 回まで)、毎回 行ベクトルと行列の乗算は、行のすべての要素がゼロ以外になるまで実行されます。この計算の複雑さは O(n³) です。 🎜 🎜フロイド・ウォーシャル🎜 🎜最短経路アルゴリズム🎜Floyd-Warshal🎜で再帰関係を調整します。これは、この質問の為替レート変換にも使用できます。 🎜フロイド-ウォーシャル🎜の複雑さはΘ(n³)です。したがって、行列の乗算は高速になる可能性があります。 🎜 リーリー 🎜どちらのアルゴリズムも為替レート行列を保存する必要があるため、空間複雑度は Θ(n²) です。 🎜トリプルの配列が提供された場合、x->y 為替レートを計算するための最適解を生成します: 有向グラフ最短経路アルゴリズム
毎回異なるトリプル配列を指定した場合、取得する必要がある結果は 1 つだけです: 有向グラフ経路探索アルゴリズム
タプルは辞書のキーとして使用できます
リーリー上記のアルゴリズムの一部は作成が非常に複雑です。簡単なアルゴリズムを書いてみましょう。 リーリー
テスト結果は次のとおりです:リーリー
ここで使用されるのは通貨名の一意性です。結合される 2 つの通貨は一意である必要があります。