Let’s first take a look at the relationship between the 8 kinds of sorting:
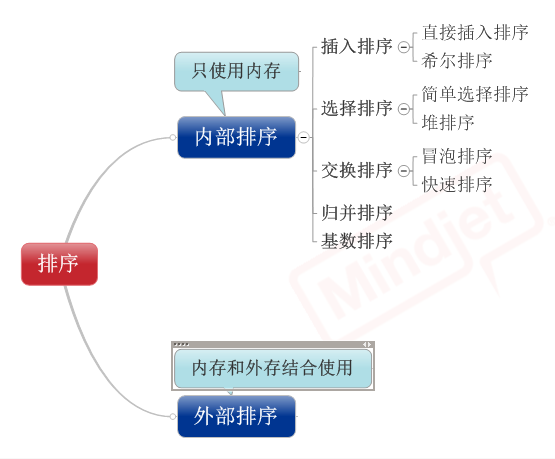
The following picture is a comparison of various sorts:
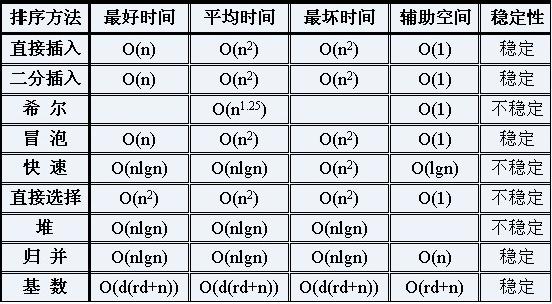
1, direct insertion sorting
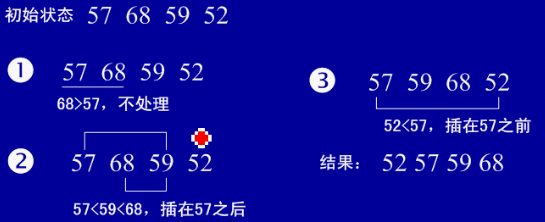
(1) Basic idea: In a set of numbers to be sorted, assuming that the previous (n-1) [n>=2] numbers are already in order, now the nth number needs to be inserted into the previous ordered numbers. , so that these n numbers
are also sorted. Repeat this cycle until everything is in order.
In the insertion algorithm, if there is a smallest number at the end of the array, the insertion algorithm will move from the last
position to the first.
(2) Example
package cglib;
public class StringNumber {
public static void insertSort(int[] a) {
if (a == null || a.length < 2) {
return;
}
int length=a.length; //数组长度
int j; //当前值的位置
int i; //指向j前的位置
int key; //当前要进行插入排序的值
//从数组的第二个位置开始遍历值
for(j=1;j<length;j++){
key=a[j];
i=j-1;
System.out.println(" 将i="+i);
//a[i]比当前值大时,a[i]后移一位,空出i的位置,好让下一次循环的值后移
while(i>=0 && a[i]>key){
System.out.println("进 i="+i);
a[i+1]=a[i]; //将a[i]值后移
i--; //i前移
System.out.println(" i="+i);
}//跳出循环(找到要插入的中间位置或已遍历到0下标)
System.out.println(" 退出while");
System.out.println(" i="+i);
a[i+1]=key; //将当前值插入
}
}
public static void main(String[] args) {
int[] array = { 3, -1, 0, -8, 2, 1 };
ArrayUtils.printArray(array);
insertSort(array);
ArrayUtils.printArray(array);
}
}
class ArrayUtils {
public static void printArray(int[] array) {
System.out.print("{");
for (int i = 0; i < array.length; i++) {
System.out.print(array[i]);
if (i < array.length - 1) {
System.out.print(", ");
}
}
System.out.println("}");
}
} Output:
Output: {3, -1, 0, -8, 2, 1}
将i=0
进 i=0
i=-1
退出while
i=-1
将i=1
进 i=1
i=0
退出while
i=0
将i=2
进 i=2
i=1
进 i=1
i=0
进 i=0
i=-1
退出while
i=-1
将i=3
进 i=3
i=2
退出while
i=2
将i=4
进 i=4
i=3
进 i=3
i=2
退出while
i=2
{-8, -1, 0, 1, 2, 3}Basic algorithm:
First divide the entire sequence of elements to be sorted into several sub-elements Sequences (composed of elements separated by a certain "increment") are directly inserted and sorted, and then the increments are reduced in sequence and then sorted. When the elements in the entire sequence are basically in order (the increment is small enough), the entire sequence is sorted. The elements undergo a direct insertion sort. Because direct insertion sorting is very efficient when the elements are basically ordered (close to the best case), Hill sorting has a greater time efficiency than the first two methods. The choice of step size is an important part of Hill sorting. Any sequence of step sizes will work as long as the final step size is 1.
The algorithm initially sorts with a certain step size, then continues to sort with a certain step size, and finally the algorithm sorts with a step size of 1. When the step size is 1, the algorithm changes to insertion sort, which ensures that the data will be sorted. Donald Shell initially suggested choosing a step size of frac{n}{2} and halving the step size until the step size reaches 1. Although this approach can be better than mathcal{O}(n^2)-like algorithms (insertion sort), there is still room for reducing the average time and worst time.
Hill sorting example: an array of n=10 58 27 32 93 65 87 58 46 9 65, with a step size of n/2.为 The first sorting step is 10/2 = 5
58 27 32 93 65 87 58 46 9 65
1B2A 2A 3A 3A 3B
4A 4B 5A 5B
, with 5 as the step size, (1A,1B), (2A,2B), (3A,3B), etc. as grouping marks. The uppercase letters indicate which element of the group it is. The same numbers indicate that they are in the same group, so Divide it into 5 groups, namely (58,87), (27,58), (32,46), (93,9), (65,65), and then perform direct insertion sorting on each group. After sorting, there are 5 groups For (58,87), (27,58), (32,46), (9,93), (65,65), the group sorting just becomes the following table within each group, the same below.
The second sorting step is 5/2 = 2
32 9 58 27 58 46 65 65 93 87 1A 1B 1C 1D 1E 1F 1G 1H 1I 1J The fourth sorting step is 1/2 = 0 to get the ordered element sequence
9 27 32 46 58 58 65 65 87 93
希尔排序的时间性能优于直接插入排序的原因:
①当文件初态基本有序时直接插入排序所需的比较和移动次数均较少。
②当n值较小时,n和n2的差别也较小,即直接插入排序的最好时间复杂度O(n)和最坏时间复杂度0(n2)差别不大。
③在希尔排序开始时增量较大,分组较多,每组的记录数目少,故各组内直接插入较快,后来增量di逐渐缩小,分组数逐渐减少,而各组的记录数目逐渐增多,但由于已经按di-1作为距离排过序,使文件较接近于有序状态,所以新的一趟排序过程也较快。
增量序列的选择:Shell排序的执行时间依赖于增量序列。
好的增量序列的共同特征(查到的资料都这么讲):
① 最后一个增量必须为1;
② 应该尽量避免序列中的值(尤其是相邻的值)互为倍数的情况。
package cglib;
public class StringNumber {
public static void main(String[] args) {
int[] arr = new int[]{44,33,99,10,30,20,59,78,23,48};
System.out.print("排序前:");
for(int o: arr) {
System.out.print(o+" ");
}
System.out.println();
shellSort(arr);
System.out.print("排序后:");
for(int o: arr) {
System.out.print(o+" ");
}
System.out.println();
}
private static void shellSort(int[] arr) {
int j;
int len = arr.length;
for(int val=len>>1; val>0; val>>=1) {
//下面是对本次的所有分组做直接插入排序
for(int i=val; i<len; i++) {
System.out.println("for:i="+i);
System.out.println("for:arr[i]="+arr[i]);
System.out.println("for:val="+val);
int temp = arr[i];
/*
* 为什么每次都用temp比较呢?
* 因为直接插入就是找到temp的合适位置。
* 为什么temp<arr[j-val]这个条件可以放在for内呢?
* 因为原来的组内数据已经有序,找到位置就停止便是。
*
*/
for(j=i; j>=val&&temp<arr[j-val]; j-=val) {
System.out.println("er:j="+j);
System.out.println("er:arr[j]="+arr[j]);
System.out.println("er:j-val="+(j-val));
System.out.println("er:arr[j-val]="+arr[j-val]);
/*
* 为什么是arr[j-val]不是arr[j]呢?
* 因为j=i开始的,而且条件是j>=val&&temp<arr[j-val]
*/
arr[j] = arr[j-val];
System.out.println("赋值er:arr[j]="+arr[j]);
}
/*
* 注意不是arr[i] = temp
* 直接插入排序也是这样的。
* 为什么呢?
* 因为j是位置,i是待插入元素
*/
arr[j] = temp;
}
}
}
}输出:
排序前:44 33 99 10 30 20 59 78 23 48 for:i=5 for:arr[i]=20 for:val=5 er:j=5 er:arr[j]=20 er:j-val=0 er:arr[j-val]=44 赋值er:arr[j]=44 for:i=6 for:arr[i]=59 for:val=5 for:i=7 for:arr[i]=78 for:val=5 er:j=7 er:arr[j]=78 er:j-val=2 er:arr[j-val]=99 赋值er:arr[j]=99 for:i=8 for:arr[i]=23 for:val=5 for:i=9 for:arr[i]=48 for:val=5 for:i=2 for:arr[i]=78 for:val=2 for:i=3 for:arr[i]=10 for:val=2 er:j=3 er:arr[j]=10 er:j-val=1 er:arr[j-val]=33 赋值er:arr[j]=33 for:i=4 for:arr[i]=30 for:val=2 er:j=4 er:arr[j]=30 er:j-val=2 er:arr[j-val]=78 赋值er:arr[j]=78 for:i=5 for:arr[i]=44 for:val=2 for:i=6 for:arr[i]=59 for:val=2 er:j=6 er:arr[j]=59 er:j-val=4 er:arr[j-val]=78 赋值er:arr[j]=78 for:i=7 for:arr[i]=99 for:val=2 for:i=8 for:arr[i]=23 for:val=2 er:j=8 er:arr[j]=23 er:j-val=6 er:arr[j-val]=78 赋值er:arr[j]=78 er:j=6 er:arr[j]=78 er:j-val=4 er:arr[j-val]=59 赋值er:arr[j]=59 er:j=4 er:arr[j]=59 er:j-val=2 er:arr[j-val]=30 赋值er:arr[j]=30 for:i=9 for:arr[i]=48 for:val=2 er:j=9 er:arr[j]=48 er:j-val=7 er:arr[j-val]=99 赋值er:arr[j]=99 for:i=1 for:arr[i]=10 for:val=1 er:j=1 er:arr[j]=10 er:j-val=0 er:arr[j-val]=20 赋值er:arr[j]=20 for:i=2 for:arr[i]=23 for:val=1 for:i=3 for:arr[i]=33 for:val=1 for:i=4 for:arr[i]=30 for:val=1 er:j=4 er:arr[j]=30 er:j-val=3 er:arr[j-val]=33 赋值er:arr[j]=33 for:i=5 for:arr[i]=44 for:val=1 for:i=6 for:arr[i]=59 for:val=1 for:i=7 for:arr[i]=48 for:val=1 er:j=7 er:arr[j]=48 er:j-val=6 er:arr[j-val]=59 赋值er:arr[j]=59 for:i=8 for:arr[i]=78 for:val=1 for:i=9 for:arr[i]=99 for:val=1 排序后:10 20 23 30 33 44 48 59 78 99
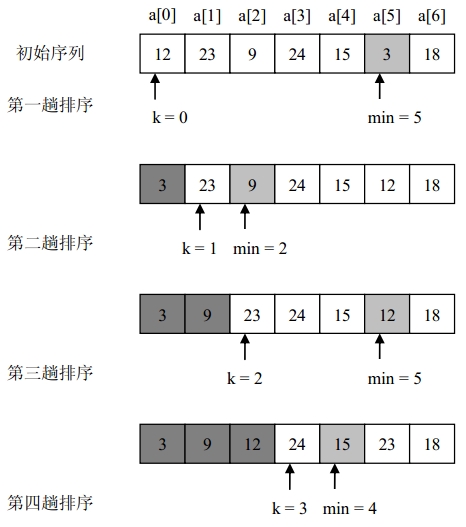
选择排序
每一趟从待排序的数据元素中选出最小(或最大)的一个元素,顺序放在已排好序的数列的最后,直到全部待排序的数据元素排完。
package cglib;
import java.util.Arrays;
import java.util.Date;
import java.util.Random;
public class StringNumber {
public static void main(String[] args){
Random random = new Random();
int[] array = new int[2000];
for (int j = 0; j < 2000; j++) {
array[j] = random.nextInt(100000);
}
System.out.println(Arrays.toString(array));
selectSortTest(array);
System.out.println(Arrays.toString(array));
}
public static void selectSortTest(int a[]) {
Date dateStart = new Date();
selectSort(a);
Date dateEnd = new Date();
System.out.println("选择排序耗费时间:"
+ (dateEnd.getTime() - dateStart.getTime()));
}
public static void selectSort(int a[]){
int n = a.length;
for(int k=0; k<n-1; k++) {
int min = k;
for(int i=k+1; i<n; i++) {//找出最小值
if(a[i] < a[min]) {
min = i;
}
}
if(k != min) {
int temp = a[k];
a[k] = a[min];
a[min] = temp;
}
}
}
}



