JS Tutorial--Knapsack Capacity Problem of Dynamic Programming Algorithm

Knapsack problem

Question
Given N items and a backpack with a capacity of V, item The volume of i is wi and its value is ci.
(There is only one of each item)
Q: How to choose the items to put in the backpack so that the total value of the items put in the backpack is the maximum?

Faced with each item, we only have two choices: put it in or not put it in. Each item can only be put in once.

Let’s try the same idea as before
Assuming that there is only the last item left, we have two options
1. When there is enough space left, choose to put it in
2. When the remaining space is insufficient,

is not put in. So we have two optimal substructures:
1. The optimal way to put i-1 items into a backpack with a capacity of V Choose
2. The optimal choice to put i-1 items into a backpack with a capacity V-w[i]

So, in summary, it is:
i The optimal choice of putting items into a backpack with capacity V:
max (The optimal choice for putting i-1 items into a backpack with capacity V, and putting i-1 items into a backpack with capacity V-w[i] -The optimal choice of 1 item c[i])

We use f[i][v] to represent the maximum value that can be obtained by putting the first i items into a backpack with capacity v.
Define the state using sub-problems:
The state transition equation is: f[i] [v] = max{f[i-1] [v],f[i-1] [v-w[ i]] c[i]}.

Let us first assume that
The total capacity of the backpack is V = 12
The capacity array of items is w = [4, 6, 2, 2, 5, 1]
The value array is c = [8, 10, 6, 3, 7, 2]

1. f(i,v) = 0 (i

2. f(i,v) = c[0] (i==1, v>=p[0]);

3. f(i,v) = f(i-1,v) (i>1, v

4. f(i,v) = max(f(i-1,v), f(i-1,v-w[i-1]) c[i-1])(i> 1, v>=w[i-1])

##We save the previous data from left to right each time

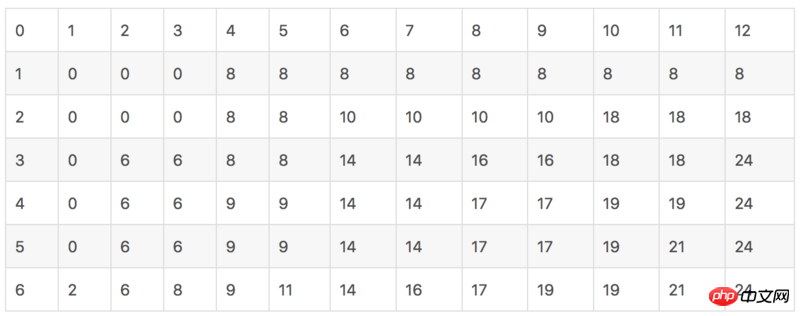
When going from top to bottom, save the data of the previous row
So in general we only need to save one row of data, and the space complexity is O(V)
The time complexity is O(N*V) , the space complexity is O(V);

However, if we use the original recursive method, that is, the permutation and combination method,

the time complexity is O(2^N);

Then when V is very large and N is small, such as V=1000 and N=6, recursion only needs to be calculated 2^6=64 times, while the highly respected dynamic programming needs to calculate 1000* 6=6000 times

So, the algorithm is not absolutely good or bad, the key depends on the application situation

Related recommendations:

JS implements dynamic programming backpack algorithm

JavaScript advanced algorithm dynamic programming example analysis

The above is the detailed content of JS Tutorial--Knapsack Capacity Problem of Dynamic Programming Algorithm. For more information, please follow other related articles on the PHP Chinese website!