튜플

또 다른 순서 목록을 tuple: tuple이라고 합니다. 튜플은 목록과 매우 유사하지만 일단 초기화되면 튜플을 수정할 수 없습니다. 그렇다면 수정할 수 없다는 것은 무엇을 의미합니까?

튜플 불변성이란 튜플을 생성할 때 변경할 수 없다는 뜻입니다. 즉, add(), insert() 같은 메서드는 없지만 인덱스 값을 얻는 메서드도 있지만, 과제를 할 수 없습니다. 그렇다면 왜 튜플이 있는 걸까요? 튜플은 불변이기 때문에 코드가 더 안전합니다. 따라서 가능하면 리스트 대신 튜플을 사용하는 것이 좋습니다.

1. 튜플 만들기

튜플을 만드는 방법은 매우 간단합니다. 괄호 안에 요소를 추가하고 쉼표로 구분하면 됩니다.

tuple1=('两点水','twowter','liangdianshui',123,456)
tuple2='两点水','twowter','liangdianshui',123,456

빈 튜플 만들기

tuple3=()

튜플에 요소가 하나만 포함되어 있는 경우 요소 뒤에 쉼표를 추가해야 합니다

tuple4=(123,)

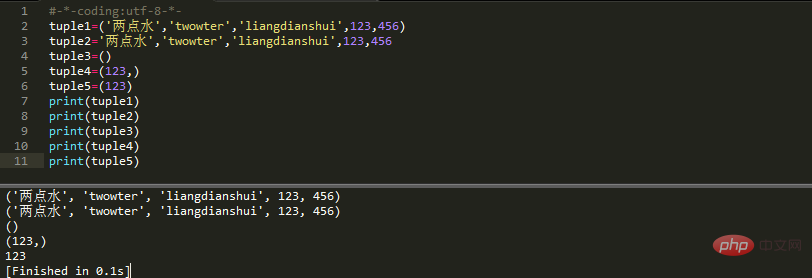
쉼표를 추가하지 않으면 생성되는 것은 튜플(튜플)이 아니라, 숫자 123은 수학 공식에서 괄호()가 튜플과 괄호를 모두 나타낼 수 있어 모호성이 생기기 때문입니다. 따라서 Python에서는 이 경우 괄호에 따라 계산이 수행되며 계산 결과는 당연히 123이 된다고 규정하고 있습니다. 구체적으로 아래 그림에서 튜플4와 튜플5의 출력값을 보면

2, 튜플(tuple)의 인덱스

튜플 첨자 인덱스는 0부터 시작해서 가로챌 수 있는데, 결합 등

3. 튜플(tuple)에 액세스

tuple(tuple)은 튜플의 값에 액세스하기 위해 첨자 인덱스를 사용할 수 있습니다.

#-*-coding:utf-8-*-
tuple1=('两点水','twowter','liangdianshui',123,456)
tuple2='两点水','twowter','liangdianshui',123,456
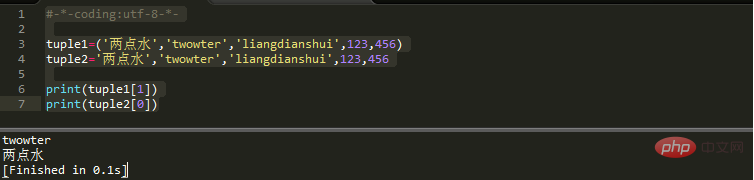
print(tuple1[1])
print(tuple2[0])

출력 결과:

4.

튜플은 불변이라고 말하면서 긴 단락을 쓰지 않았나요? 여기서 튜플이 다시 수정되는 이유는 무엇입니까? 튜플에 포함된 요소 값은 수정이 허용되지 않지만 튜플을 연결하고 결합할 수 있으며, 다른 목록의 값을 수정하여 튜플의 값에 영향을 미칠 수 있기 때문입니다.

구체적으로 다음 예를 보면:

#-*-coding:utf-8-*-
list1=[123,456]
tuple1=('两点水','twowater','liangdianshui',list1)
print(tuple1)
list1[0]=789
list1[1]=100
print(tuple1)

출력 결과:

('两点水', 'twowater', 'liangdianshui', [123, 456])
('两点水', 'twowater', 'liangdianshui', [789, 100])

두 번 출력된 튜플 값이 변경된 것을 확인할 수 있습니다. Tuple1이 어떻게 저장되는지 살펴보겠습니다.

튜플 흐름도 수정

튜플1에 4개의 요소가 있고 마지막 요소는 List이고 List의 두 요소 124와 456을 789로 수정하면 List에 두 개의 요소가 있는 것을 볼 수 있습니다. 100, tuple1의 출력 값으로 판단하면 실제로 변경된 것처럼 보이지만 실제로 변경된 것은 tuple의 요소가 아니라 목록의 요소입니다. 처음에 튜플이 가리키는 목록은 다른 목록으로 변경되지 않았습니다. 따라서 소위 튜플의 "변경되지 않음"은 튜플의 각 요소가 결코 변경되지 않음을 의미합니다. tupe1의 네 번째 요소는 여전히 원래 목록을 가리키며 변경되지 않은 상태로 유지됩니다.

5. 튜플 삭제

튜플 튜플에 포함된 요소 값은 삭제할 수 없지만 del 문을 사용하면 튜플 전체를 삭제할 수 있습니다

#-*-coding:utf-8-*-
tuple1=('两点水','twowter','liangdianshui',[123,456])
print(tuple1)
del tuple1

6 튜플(tuple) 연산자

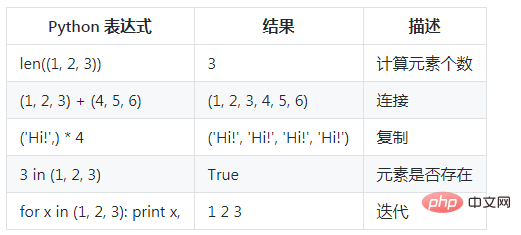
는 문자열과 동일합니다. , 튜플 사이 + 기호와 * 기호를 사용하여 작업을 수행할 수 있습니다. 이는 이들을 결합하고 복사하여 새로운 튜플을 생성할 수 있음을 의미합니다.

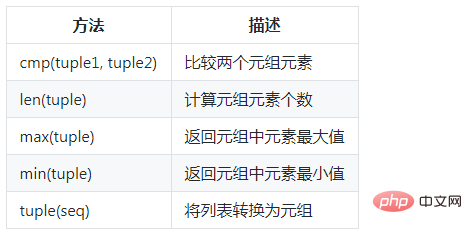
7. 튜플 내장 함수