python实现汉诺塔递归算法经典案例

    学到递归的时候有个汉诺塔的练习，汉诺塔应该是学习计算机递归算法的经典入门案例了，所以本人觉得可以写篇博客来表达一下自己的见解。这markdown编辑器还不怎么会用，可能写的有点格式有点丑啦，各位看官多多见谅.
　网上找了一张汉诺塔的图片，汉诺塔就是利用用中间的柱子把最左边的柱子上的圆盘依次从大到小叠上去，说白了就是c要跟原来的a一样 

 

废话少说，先亮代码

def move(n, a, buffer, c):
  if(n == 1):
    print(a,"->",c)
    return
  move(n-1, a, c, buffer)
  move(1, a, buffer, c)
  move(n-1, buffer, a, c)
move(3, "a", "b", "c")

　 首先是定义了一个移动的函数,四个参数分别代表，a柱上的盘子个数，buffer也就是b柱，命名为buffer便于理解，顾名思义就是一个a移动到c的缓冲区.然后c就是目标柱子
下面我们来读函数代码
　递归的一般写法，肯定有个中止递归循环的条件，所以在判断a柱上的盘子个数为1的时候既可以中止递归并返回,a柱上面只有一个的时候肯定就是把a移动到c了，重点是下面的代码，递归其实是一种很抽象的算法，我们要利用抽象思维去想汉诺塔这个问题，把a柱上的盘子想成两份，就是上面的盘子和最底下的盘子，如果所示

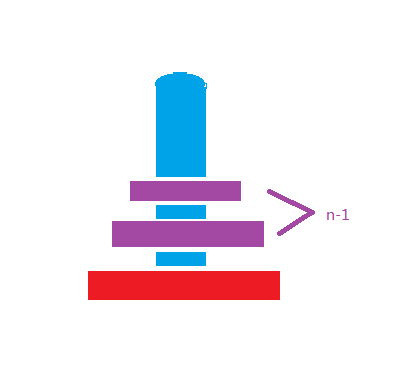
　我们不关心上面的盘子到底有几个，我们每次的操作就是把最底下的盘子通过缓冲区 b柱 buffer 移动到c柱。
　童鞋们肯定在想为啥要酱紫移动呢，其实这是一种总结归纳吧，你自己玩一下汉诺塔游戏就会发现规律，其实这个游戏就是不停的把上面的所有的想方设法的移到b上，然后把a最后最大的那个弄到c,然后再绞尽脑汁的把b上的移动到c，这时候你就发现，原来b上的也要先通过空的也就是a来存放当前b上面的n-1个，然后把b的最大最后的移动到c，这里规律就体现出来了，也可以抽象出移动的方法，并可以以此设计出程序算法.

　以下我们来利用刚才的抽象思维解读剩余代码

move(n-1, a, c, buffer)

这段代码就是表示把刚才所说的a柱的上面的n-1个，通过c按照从小到大的规则先移动到缓冲区buffer。此函数进入递归。

move(1, a, buffer, c)

当上面的语句执行完成，也就是n-1个盘子的递归移动完成之后，执行此语句，就是把a柱上的一个盘子移动到c,也就是所谓的最底下的盘子

move(n-1, buffer , a, c)

最后一步，就是刚才把a上面的n-1个都移动到了buffer上面，肯定要通过a移动到c才能完成整个汉诺塔的移动啊，于是最后一步自然是把刚才的n-1个通过a当缓冲区移动到c柱上.
　我来写下整个移动流程，以a柱上有3个为例子

/**
我把3个盘子的汉诺塔全部通过代码演示，按缩进原则，每一个缩进即进一个递归函数，每打印一次即中止当前递归,也就是每个print
说明:
  1.n = 3, n = 2, n = 1是每次执行if(n == 1)的结果，这里就不写判断了，相信童鞋们也能看懂，也就是n不等与1时就减1进入递归
  2.请注意a,b,c柱每次进入函数的顺序，不要被形参带错路了，看准每次函数参数的实参 
**/
move(3, "a", "b", "c")
n=3:
  //开始从a上移动n-1即2个盘子通过c移动到b,以腾出c供a最后一个盘子移动
  move(2, "a","c","b")
  n=2:
  //开始进行n=2的一个递归，把当前a('a')柱上的n-1个盘子通过c('b'）移动到b('c')
    move(1, "a", "b", "c")
    n=1:
    //n=2的第一个递归完成,打印结果，执行当前子函数剩余代码
      print("a", "->", "c") 
    move(1, "a", "c", "b")
    n=1:
      print("a", "->", "b")
    move(1, "c", "a", "b")
    n=1:
      print("c", "->", "b")
  　  //到这里完成了a柱上面的n-1即是2个盘子的移动
//开始把a柱上最后一个盘子移动到c柱上
move(1, "a", "b", "c")
n=1:
  print("a", "->", "c")
  //到这里完成移动a柱上的最后一个盘子到c柱上 
move(2, "b", "a", "c")
n=2:
//开始进行n=2的第二个递归,即把当前b('b')的盘子(n-1个)通过a('a')移动到c('c')上
  move(1, "b", "c", "a")
  n=1:
  //n=2 的第二个递归完成，打印结果并执行当前子函数的剩余代码
    print("b", "->", "a")
  move(1, "b", "a", "c")
  n=1:
    print("b", "->", "c")
  move(1, "a", "b", "c")
  n=1:
    print("a", "->", "c")
    //到这里把b上的盘子通过a移动到c,
//整个代码执行完毕,汉诺塔移动完成

最后的打印结果为:

童鞋们理解了汉诺塔的递归算法原理后，可以写个程序来试试，这里只是学到Python的递归所以用了Python，童鞋们可以用其他语言实现，汉诺塔确实能帮助理解递归原理，递归在程序设计中的重要性不言而喻啦！

본 웹사이트의 성명

본 글의 내용은 네티즌들의 자발적인 기여로 작성되었으며, 저작권은 원저작자에게 있습니다. 본 사이트는 이에 상응하는 법적 책임을 지지 않습니다. 표절이나 침해가 의심되는 콘텐츠를 발견한 경우 admin@php.cn으로 문의하세요.