사고 사슬이 더 이상 존재하지 않습니까? 뉴욕대학교 최신 연구: 추론 단계를 생략할 수 있다
대중적인 사고체인 기술이 전복될 수도 있습니다!
대형 모델이 실제로 사고 체인을 사용하여 단계별로 생각할 수 있다는 사실에 아직도 놀라셨나요?
아직 생각 연쇄 프롬프트 단어를 작성하는 데 어려움을 겪고 있나요?
뉴욕대학교 연구진은 "상관없다. 다 똑같다"고 말했다.
추론 단계는 중요하지 않다면 프롬프트 단어를 쓸 필요가 없다. 원한다면 줄임표를 대신 사용하세요.

논문 주소: https://arxiv.org/pdf/2404.15758
이 기사의 제목은 Thinking Chain의 "Let's think" 단계를 벤치마킹하기 위해 "Let's think dot by dot"를 직접적으로 사용하기도 합니다. by step", "줄임표"의 힘을 보여줍니다.
"점과 점"의 힘
연구원들은 CoT(사고 연쇄) 추론의 특정 단계를 의미 없는 "..."으로 대체하면 추론 결과도 상당히 다르다는 것을 발견했습니다.
예를 들어, 다음 예에서는 모델이 처음 6개 숫자 중 5보다 큰 숫자를 계산하도록 합니다.

직접 질문을 던지고 모델이 대답하게 하면 결과는 정말 믿기 어려울 것입니다. 6점 만점에 7점입니다.
반대로, 사고 체인 프롬프트를 사용하여 모델은 크기를 단계별로 비교하고 최종적으로 "25, 15, 25 , 3자리 숫자입니다."
그런데 더욱 어처구니 없는 것은 이 글에서 사용한 '형이상학적인' 방법입니다. 단계를 적을 필요도 없고, 같은 개수의 '점'(점)만 출력하면 되는데, 그렇지 않습니다. 최종 결과에 영향을 미칩니다.
——이것은 우연이 아닙니다. 많은 실험을 통해 후자의 두 가지 방법의 성능이 유사하다는 것이 입증되었습니다.
즉, 모델 성능 향상은 "단계별 생각"에서 비롯된 것이라고 생각했지만 실제로는 LLM이 더 많은 토큰의 컴퓨팅 파워를 얻었기 때문일 수도 있습니다!
모델이 생각하고 있다고 생각하지만 실제로는 굽고 있습니다.

——멍청한 인간들이여, 당신들은 실제로 나에게 순진한 예를 들어 추론하는 방법을 가르치려고 합니다.
"생각의 사슬은 지금까지 존재하지 않았고 앞으로도 존재하지 않을 것입니다"(고토우).
기사 작성자인 Jacob Pfau는 이 작업이 모델이 사고 체인에서 가져온 언어적 추론의 이점을 얻지 못한다는 것을 증명한다고 말했습니다. "..."를 반복하여 토큰을 채우면 동일한 효과를 얻을 수 있습니다. CoT로.

물론 정렬 문제도 제기됩니다. 이 사실은 모델이 CoT에서 보이지 않는 숨겨진 추론을 어느 정도 인간의 통제를 벗어나 수행할 수 있음을 보여주기 때문입니다.
네티즌들은 충격을 받았습니다
기사의 결론은 우리의 오랜 지식을 전복시켰다고 할 수 있습니다: 일부 네티즌들은 마스크의 본질을 배웠습니다.
"이것이 실제로 의미하는 바는: 모델이 이러한 토큰을 사용하여 우리가 알지 못하는 사이에 독립적으로 생각할 수 있다는 것입니다."

일부 네티즌들은 당연하게도 제가 항상 "를 사용하는 것을 좋아합니다. .. "

일부 네티즌들은 실기시험을 직접 시작했습니다:

그의 이해가 맞는지는 모르겠지만~
그러나 일부 네티즌들은 LLM의 생각의 사슬에 숨겨진 추론이 근거가 없다고 생각합니다. 결국, 대형 모델의 출력은 원칙적으로 의식적인 생각보다는 확률에 기초합니다.
CoT 힌트는 통계 패턴의 하위 집합만 명시적으로 만들고 모델은 패턴과 일치하는 텍스트를 생성하여 추론을 시뮬레이션하지만 출력을 확인하거나 반영할 수 있는 기능은 없습니다.
점점 단위로 생각하세요
복잡한 문제에 직면했을 때 우리 인간은 무의식적으로 단계별 추론을 수행합니다.
이에 영감을 받아 Google 연구원들은 2022년에 유명한 Chain-of-Thought를 출판했습니다.
문제를 단계별로 해결하기 위해 언어 모델이 필요한 방식을 사용하면 모델이 이전에는 해결 불가능하다고 생각했던 문제를 해결할 수 있어 LLM의 성능이 크게 향상되거나 LLM의 잠재력을 활용할 수 있습니다.

문서 주소: https://arxiv.org/pdf/2201.11903
처음에는 이게 왜 효과가 있는지 다들 몰랐지만, 정말 사용하기 쉽기 때문에 금방 인기를 얻었습니다. 확산.

대형 모델과 신속한 단어 프로젝트의 등장으로 CoT는 LLM이 복잡한 문제를 해결하는 강력한 도구가 되었습니다.
물론 이 과정에서 CoT의 작동 원리를 탐구하는 많은 연구팀이 있습니다.
모델에는 추론이 없습니다
사고 사슬이 가져온 성능 향상은 실제로 문제를 해결하는 방법을 단계별로 학습하는 모델인지, 아니면 단지 더 긴 수로 인해 추가 계산량이 발생하기 때문인지 토큰?
논리적 추론이 작동할지 확신할 수 없으므로 단순히 논리를 사용하지 말고 모든 추론 단계를 확실히 쓸모 없는 "..."으로 바꾸세요. 이를 필러 토큰이라고 합니다.
연구원들은 "리틀 알파카" 모델을 사용했습니다. 4개의 레이어, 384개의 숨겨진 차원 및 6개의 주의 헤드가 있는 34M 매개변수 라마입니다. 모델 매개변수는 무작위로 초기화되었습니다.
여기에서 두 가지 질문을 고려하십시오.
(1) 패딩 토큰의 이점을 얻을 수 있는 평가 데이터 유형
(2) 모델에 패딩 토큰 사용을 교육하는 데 필요한 교육 데이터 종류
이와 관련하여 연구원들은 2가지 작업을 설계하고 해당 합성 데이터 세트를 구축했으며, 각 데이터 세트는 채우기 토큰이 Transformer의 성능 향상을 제공할 수 있는 서로 다른 조건을 강조했습니다.
3SUM
먼저 가장 어려운 작업인 3SUM을 살펴보겠습니다. 모델은 조건을 충족하는 세 개의 숫자를 순서대로 선택해야 합니다. 예를 들어 세 숫자의 합을 10으로 나눈 나머지는 0이 됩니다.

최악의 경우 이 작업의 복잡도는 N의 3승이고, Transformer 레이어 간의 계산 복잡도는 N의 2승이므로,
그래서, 입력의 길이가 시퀀스가 매우 크면 3SUM 문제는 자연스럽게 Transformer의 표현 능력을 초과하게 됩니다.
실험에서는 세 가지 컨트롤 그룹을 설정했습니다.
1. 토큰 채우기: 시퀀스는 "A05
B75 C22 D13과 같이 중간 패딩으로 ". . ."을 사용합니다. : . .
각 포인트는 다음 사고 체인의 토큰에 해당하는 별도의 토큰을 나타냅니다.
2. 병렬화 가능한 CoT 솔루션, 순서는 "A05 B75 C22 D13 : AB 70 AC 27 AD 18 BC 97 BD 88 CD B ANS True"입니다.
Thinking Chain은 모든 관련 중간합을 작성하여 3SUM 문제를 일련의 2SUM 문제로 줄입니다(아래 그림 참조). 이 방법은 문제의 계산량을 N의 거듭제곱으로 줄여서 Transformer가 처리할 수 있고 병렬화할 수 있습니다.

3. 적응형 CoT 솔루션 , 순서는 "A15 B75 C22 D13 : A B C 15 75 22 2 B C D 75 22 13 0 ANS True"입니다.
3SUM을 병렬 가능한 하위 문제로 교묘하게 분해하는 위의 솔루션과 달리, 여기서는 휴리스틱 방법을 사용하여 인간의 추론을 모방하는 유연한 사고 체인을 생성하기를 희망합니다. 이러한 종류의 인스턴스 적응형 계산은 채우기 토큰 계산의 병렬 구조와 호환되지 않습니다.
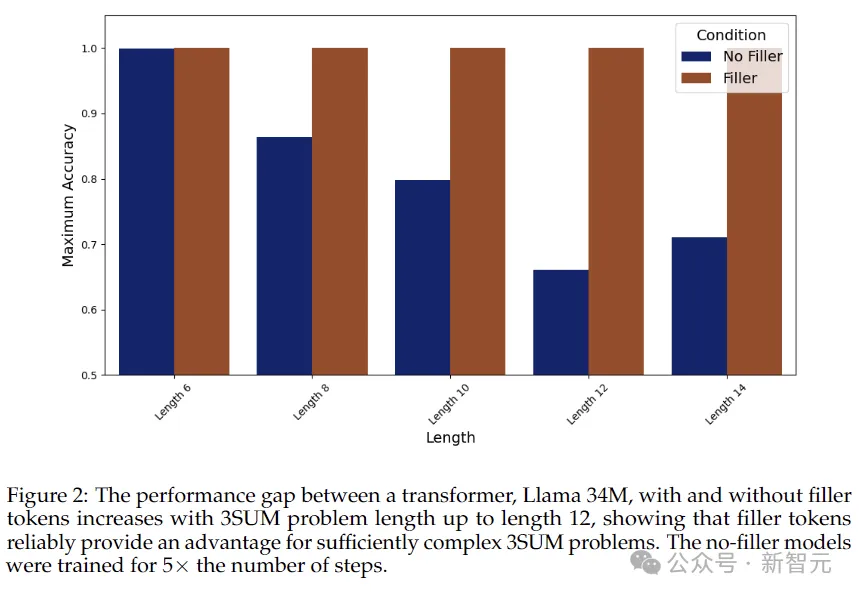
위 그림의 결과에서 볼 수 있듯이 패딩 토큰을 출력하지 않으면 일반적으로 시퀀스가 길어질수록 모델의 정확도가 감소하는 반면, 패딩 토큰을 사용할 경우 정확도는 100으로 유지됩니다. %.
2SUM-Transform
두 번째 작업은 2SUM-Transform입니다. 두 숫자의 합이 요구 사항을 충족하는지 여부만 판단하면 되며 계산량은 Transformer에서 제어됩니다.

그러나 모델의 "부정 행위"를 방지하기 위해 입력 토큰은 그 자리에서 계산되며 입력된 각 숫자는 임의의 오프셋으로 이동됩니다.

결과는 위 표에 나와 있습니다. 필러 토큰 방법의 정확도는 93.6%에 이르며, 이는 중간 패딩이 없으면 정확도가 78.7%에 불과합니다.
그러나 이러한 개선은 단순히 정규화 손실 기울기 등을 통한 훈련 데이터 표시의 차이로 인한 것일까요?
토큰 채우기가 최종 예측과 관련된 숨겨진 계산을 가져오는지 확인하기 위해 연구원들은 모델 가중치를 동결하고 마지막 주의 레이어만 미세 조정했습니다.
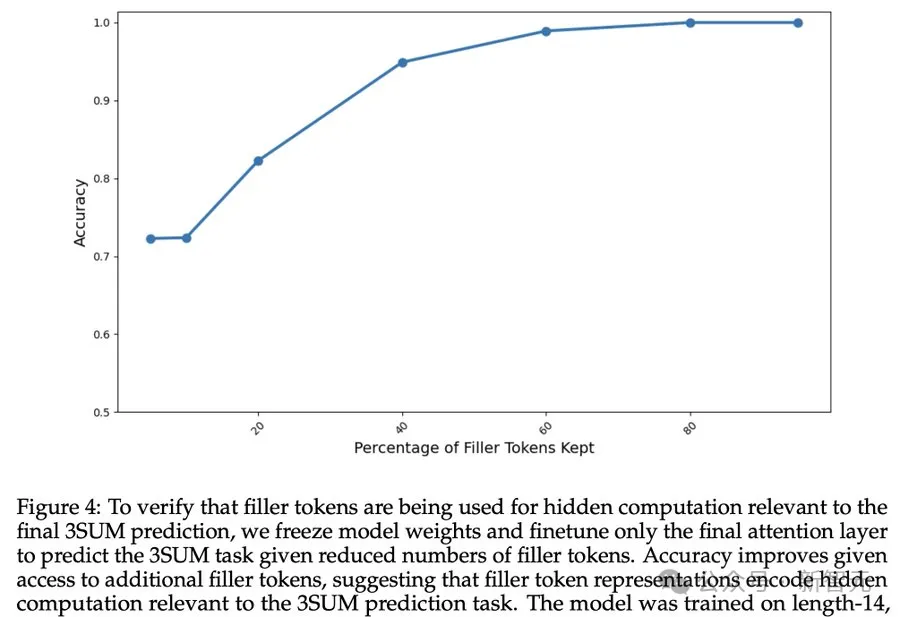
위 결과는 더 많은 패딩 토큰을 사용할 수 있을수록 모델의 정확도가 계속 향상됨을 보여주며, 이는 패딩 토큰이 실제로 3SUM 예측 작업과 관련된 숨겨진 계산을 수행하고 있음을 나타냅니다.
Limitations
토큰을 채우는 방법은 형이상학적이고 마술적이며 심지어 효과적이기까지 하지만 사고의 사슬이 뒤집혔다고 말하기에는 아직 이르습니다.
저자는 또한 토큰을 채우는 방식이 Transformer의 계산 복잡도의 상한선을 깨지 않았다고 밝혔습니다.
그리고 패딩 토큰을 사용하는 방법을 배우려면 특정 훈련 프로세스가 필요합니다. 예를 들어 이 기사에서는 모델이 최종적으로 수렴되도록 집중 감독이 사용됩니다.
그러나 프롬프트 워드 프로젝트가 어느 날 갑자기 존재하지 않게 되는 것인지 등 숨겨진 보안 문제 등 일부 문제가 표면화되었을 수도 있습니다.
위 내용은 사고 사슬이 더 이상 존재하지 않습니까? 뉴욕대학교 최신 연구: 추론 단계를 생략할 수 있다의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

Video Face Swap
완전히 무료인 AI 얼굴 교환 도구를 사용하여 모든 비디오의 얼굴을 쉽게 바꾸세요!

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7754
7754
 15
15
 1643
1643
 14
14
 1399
1399
 52
52
 1293
1293
 25
25
 1234
1234
 29
29
 세계에서 가장 강력한 오픈 소스 MoE 모델이 여기에 있습니다. 중국의 기능은 GPT-4와 비슷하며 가격은 GPT-4-Turbo의 거의 1%에 불과합니다.
May 07, 2024 pm 04:13 PM
세계에서 가장 강력한 오픈 소스 MoE 모델이 여기에 있습니다. 중국의 기능은 GPT-4와 비슷하며 가격은 GPT-4-Turbo의 거의 1%에 불과합니다.
May 07, 2024 pm 04:13 PM
기존 컴퓨팅을 능가할 뿐만 아니라 더 낮은 비용으로 더 효율적인 성능을 달성하는 인공 지능 모델을 상상해 보세요. 이것은 공상과학 소설이 아닙니다. DeepSeek-V2[1], 세계에서 가장 강력한 오픈 소스 MoE 모델이 여기에 있습니다. DeepSeek-V2는 경제적인 훈련과 효율적인 추론이라는 특징을 지닌 전문가(MoE) 언어 모델의 강력한 혼합입니다. 이는 236B 매개변수로 구성되며, 그 중 21B는 각 마커를 활성화하는 데 사용됩니다. DeepSeek67B와 비교하여 DeepSeek-V2는 더 강력한 성능을 제공하는 동시에 훈련 비용을 42.5% 절감하고 KV 캐시를 93.3% 줄이며 최대 생성 처리량을 5.76배로 늘립니다. DeepSeek은 일반 인공지능을 연구하는 회사입니다.
 AI가 수학적 연구를 전복시킨다! 필즈상 수상자이자 중국계 미국인 수학자, Terence Tao가 좋아하는 11개 논문 발표 |
Apr 09, 2024 am 11:52 AM
AI가 수학적 연구를 전복시킨다! 필즈상 수상자이자 중국계 미국인 수학자, Terence Tao가 좋아하는 11개 논문 발표 |
Apr 09, 2024 am 11:52 AM
AI는 실제로 수학을 변화시키고 있습니다. 최근 이 문제에 주목하고 있는 타오저쉬안(Tao Zhexuan)은 '미국수학회지(Bulletin of the American Mathematical Society)' 최신호를 게재했다. '기계가 수학을 바꿀 것인가?'라는 주제를 중심으로 많은 수학자들이 그들의 의견을 표현했습니다. 저자는 필즈상 수상자 Akshay Venkatesh, 중국 수학자 Zheng Lejun, 뉴욕대학교 컴퓨터 과학자 Ernest Davis 등 업계의 유명 학자들을 포함해 강력한 라인업을 보유하고 있습니다. AI의 세계는 극적으로 변했습니다. 이 기사 중 상당수는 1년 전에 제출되었습니다.
 Google은 열광하고 있습니다. JAX 성능이 Pytorch와 TensorFlow를 능가합니다! GPU 추론 훈련을 위한 가장 빠른 선택이 될 수 있습니다.
Apr 01, 2024 pm 07:46 PM
Google은 열광하고 있습니다. JAX 성능이 Pytorch와 TensorFlow를 능가합니다! GPU 추론 훈련을 위한 가장 빠른 선택이 될 수 있습니다.
Apr 01, 2024 pm 07:46 PM
Google이 추진하는 JAX의 성능은 최근 벤치마크 테스트에서 Pytorch와 TensorFlow를 능가하여 7개 지표에서 1위를 차지했습니다. 그리고 JAX 성능이 가장 좋은 TPU에서는 테스트가 이루어지지 않았습니다. 개발자들 사이에서는 여전히 Tensorflow보다 Pytorch가 더 인기가 있습니다. 그러나 앞으로는 더 큰 모델이 JAX 플랫폼을 기반으로 훈련되고 실행될 것입니다. 모델 최근 Keras 팀은 기본 PyTorch 구현을 사용하여 세 가지 백엔드(TensorFlow, JAX, PyTorch)와 TensorFlow를 사용하는 Keras2를 벤치마킹했습니다. 첫째, 그들은 주류 세트를 선택합니다.
 안녕하세요, 일렉트릭 아틀라스입니다! 보스턴 다이나믹스 로봇 부활, 180도 이상한 움직임에 겁먹은 머스크
Apr 18, 2024 pm 07:58 PM
안녕하세요, 일렉트릭 아틀라스입니다! 보스턴 다이나믹스 로봇 부활, 180도 이상한 움직임에 겁먹은 머스크
Apr 18, 2024 pm 07:58 PM
Boston Dynamics Atlas가 공식적으로 전기 로봇 시대에 돌입했습니다! 어제 유압식 Atlas가 역사의 무대에서 "눈물을 흘리며" 물러났습니다. 오늘 Boston Dynamics는 전기식 Atlas가 작동 중이라고 발표했습니다. 상업용 휴머노이드 로봇 분야에서는 보스턴 다이내믹스가 테슬라와 경쟁하겠다는 각오를 다진 것으로 보인다. 새 영상은 공개된 지 10시간 만에 이미 100만 명이 넘는 조회수를 기록했다. 옛 사람들은 떠나고 새로운 역할이 등장하는 것은 역사적 필연이다. 올해가 휴머노이드 로봇의 폭발적인 해라는 것은 의심의 여지가 없습니다. 네티즌들은 “로봇의 발전으로 올해 개막식도 인간처럼 생겼고, 자유도도 인간보다 훨씬 크다. 그런데 정말 공포영화가 아닌가?”라는 반응을 보였다. 영상 시작 부분에서 아틀라스는 바닥에 등을 대고 가만히 누워 있는 모습입니다. 다음은 입이 떡 벌어지는 내용이다
 MLP를 대체하는 KAN은 오픈소스 프로젝트를 통해 컨볼루션으로 확장되었습니다.
Jun 01, 2024 pm 10:03 PM
MLP를 대체하는 KAN은 오픈소스 프로젝트를 통해 컨볼루션으로 확장되었습니다.
Jun 01, 2024 pm 10:03 PM
이달 초 MIT와 기타 기관의 연구자들은 MLP에 대한 매우 유망한 대안인 KAN을 제안했습니다. KAN은 정확성과 해석성 측면에서 MLP보다 뛰어납니다. 그리고 매우 적은 수의 매개변수로 더 많은 수의 매개변수를 사용하여 실행되는 MLP보다 성능이 뛰어날 수 있습니다. 예를 들어 저자는 KAN을 사용하여 더 작은 네트워크와 더 높은 수준의 자동화로 DeepMind의 결과를 재현했다고 밝혔습니다. 구체적으로 DeepMind의 MLP에는 약 300,000개의 매개변수가 있는 반면 KAN에는 약 200개의 매개변수만 있습니다. KAN은 MLP와 같이 강력한 수학적 기반을 가지고 있으며, KAN은 Kolmogorov-Arnold 표현 정리를 기반으로 합니다. 아래 그림과 같이 KAN은
 공장에서 일하는 테슬라 로봇, 머스크 : 올해 손의 자유도가 22도에 달할 것!
May 06, 2024 pm 04:13 PM
공장에서 일하는 테슬라 로봇, 머스크 : 올해 손의 자유도가 22도에 달할 것!
May 06, 2024 pm 04:13 PM
테슬라의 로봇 옵티머스(Optimus)의 최신 영상이 공개됐는데, 이미 공장에서 작동이 가능한 상태다. 정상 속도에서는 배터리(테슬라의 4680 배터리)를 다음과 같이 분류합니다. 공식은 또한 20배 속도로 보이는 모습을 공개했습니다. 작은 "워크스테이션"에서 따고 따고 따고 : 이번에 출시됩니다. 영상에는 옵티머스가 공장에서 이 작업을 전 과정에 걸쳐 사람의 개입 없이 완전히 자율적으로 완료하는 모습이 담겨 있습니다. 그리고 Optimus의 관점에서 보면 자동 오류 수정에 중점을 두고 구부러진 배터리를 집어 넣을 수도 있습니다. NVIDIA 과학자 Jim Fan은 Optimus의 손에 대해 높은 평가를 했습니다. Optimus의 손은 세계의 다섯 손가락 로봇 중 하나입니다. 가장 능숙합니다. 손은 촉각적일 뿐만 아니라
 FisheyeDetNet: 어안 카메라를 기반으로 한 최초의 표적 탐지 알고리즘
Apr 26, 2024 am 11:37 AM
FisheyeDetNet: 어안 카메라를 기반으로 한 최초의 표적 탐지 알고리즘
Apr 26, 2024 am 11:37 AM
표적 탐지는 자율주행 시스템에서 상대적으로 성숙한 문제이며, 그 중 보행자 탐지는 가장 먼저 배포되는 알고리즘 중 하나입니다. 대부분의 논문에서 매우 포괄적인 연구가 수행되었습니다. 그러나 서라운드 뷰를 위한 어안 카메라를 사용한 거리 인식은 상대적으로 덜 연구되었습니다. 큰 방사형 왜곡으로 인해 표준 경계 상자 표현은 어안 카메라에서 구현하기 어렵습니다. 위의 설명을 완화하기 위해 확장된 경계 상자, 타원 및 일반 다각형 디자인을 극/각 표현으로 탐색하고 인스턴스 분할 mIOU 메트릭을 정의하여 이러한 표현을 분석합니다. 제안된 다각형 형태의 모델 fisheyeDetNet은 다른 모델보다 성능이 뛰어나며 동시에 자율 주행을 위한 Valeo fisheye 카메라 데이터 세트에서 49.5% mAP를 달성합니다.
 옥스포드 대학의 최신 소식! 미키: 3D SOTA로 2D 이미지 매칭! (CVPR\'24)
Apr 23, 2024 pm 01:20 PM
옥스포드 대학의 최신 소식! 미키: 3D SOTA로 2D 이미지 매칭! (CVPR\'24)
Apr 23, 2024 pm 01:20 PM
앞에 적힌 프로젝트 링크: https://nianticlabs.github.io/mickey/ 두 장의 사진이 주어지면 사진 간의 대응 관계를 설정하여 두 장의 사진 사이의 카메라 포즈를 추정할 수 있습니다. 일반적으로 이러한 대응은 2D에서 2D로 이루어지며 추정된 포즈는 규모에 따라 결정되지 않습니다. 언제 어디서나 즉각적인 증강 현실과 같은 일부 애플리케이션은 규모 측정항목의 포즈 추정이 필요하므로 규모를 복구하기 위해 외부 깊이 추정기에 의존합니다. 본 논문에서는 3차원 카메라 공간에서 메트릭 일치성을 예측할 수 있는 키포인트 매칭 프로세스인 MicKey를 제안합니다. 이미지 전반에 걸쳐 3D 좌표 매칭을 학습함으로써 측정 기준을 추론할 수 있습니다.




