재귀 메서드는 자신을 호출하는 메서드입니다. 많은 수학 함수는 재귀를 사용하여 정의됩니다. 간단한 예부터 시작해 보겠습니다. 숫자 n의 계승은 다음과 같이 재귀적으로 정의할 수 있습니다.
0! = 1;
N! =n × (n - 1)!; n > 0
특정 n에 대해 n!을 어떻게 찾나요? 1!을 찾는 것은 쉽습니다. 0!은 1이고 1!은 1 × 0이라는 것을 알고 있기 때문입니다. !. (n - 1)!을 알고 있다고 가정하면 n × (n - 1)!을 사용하여 즉시 n!을 얻을 수 있습니다. 따라서 n! 계산 문제는 (n - 1)! 계산으로 축소됩니다. (n - 1)!을 계산할 때 n이 0으로 줄어들 때까지 동일한 아이디어를 재귀적으로 적용할 수 있습니다.
factorial(n)을 n!을 계산하는 방법으로 가정합니다. n = 0으로 메소드를 호출하면 즉시 결과를 반환합니다. 이 방법은 기본 사례 또는 중지 조건이라고 하는 가장 간단한 경우를 해결하는 방법을 알고 있습니다. n > 0, n - 1의 계승을 계산하기 위한 하위 문제로 문제를 축소합니다. 하위 문제는 기본적으로 원래 문제와 동일하지만 더 간단하거나 더 작습니다. 하위 문제는 원래 문제와 동일한 속성을 갖기 때문에 재귀 호출이라고 하는 다른 인수를 사용하여 메서드를 호출할 수 있습니다.
factorial(n) 계산을 위한 재귀 알고리즘은 다음과 같이 간단히 설명할 수 있습니다.
if (n == 0)
1을 반환;
그 외
n * 계승(n - 1)을 반환합니다.
재귀 호출을 사용하면 더 많은 재귀 호출이 발생할 수 있습니다. 그 이유는 이 메서드가 하위 문제를 새로운 하위 문제로 계속 나누기 때문입니다. 재귀 메서드를 종료하려면 문제가 결국 중지 사례로 축소되어야 하며, 이 시점에서 메서드는 호출자에게 결과를 반환합니다. 그런 다음 호출자는 계산을 수행하고 결과를 자체 호출자에게 반환합니다. 이 프로세스는 결과가 원래 호출자에게 다시 전달될 때까지 계속됩니다. 이제 n에 계승(n - 1)의 결과를 곱하여 원래 문제를 해결할 수 있습니다.
아래 코드는 사용자에게 음이 아닌 정수를 입력하라는 메시지를 표시하고 해당 숫자의 계승값을 표시하는 완전한 프로그램을 제공합니다.

factorial 메서드(17~22행)는 본질적으로 계승에 대한 재귀적 수학적 정의를 Java 코드로 직접 변환한 것입니다. factorial에 대한 호출은 자신을 호출하기 때문에 재귀적입니다. factorial에 전달된 매개변수는 0의 기본 사례에 도달할 때까지 감소됩니다.
재귀 메서드를 작성하는 방법을 살펴보겠습니다. 재귀는 뒤에서 어떻게 작동하나요? 아래 그림은 n = 4.
으로 시작하는 재귀 호출의 실행을 보여줍니다.
재귀 호출을 위한 스택 공간 사용은 아래 그림과 같습니다.
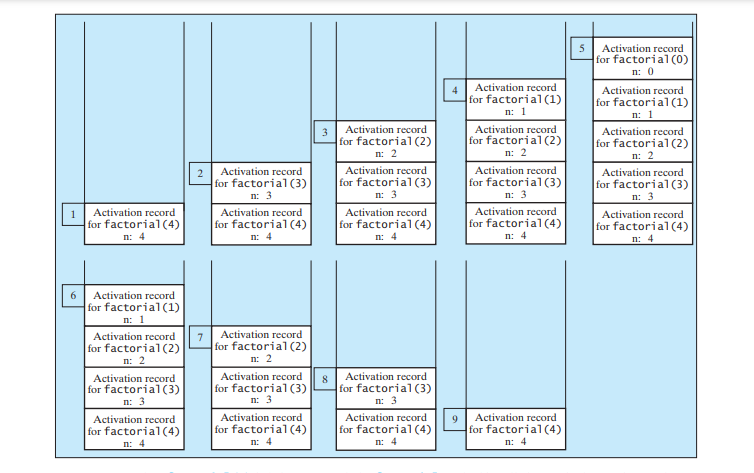
루프를 사용하여 factorial 메서드를 구현하는 것이 더 간단하고 효율적입니다. 그러나 여기서는 재귀의 개념을 보여주기 위해 재귀 계승 방법을 사용합니다. 이 장의 뒷부분에서는 본질적으로 재귀적이며 재귀를 사용하지 않고는 해결하기 어려운 몇 가지 문제를 제시할 것입니다.
재귀가 결국 기본 사례로 수렴되는 방식으로 문제를 줄이지 않거나 기본 사례가 지정되지 않은 경우 무한 재귀가 발생할 수 있습니다. 예를 들어 factorial 메소드를 다음과 같이 실수로 작성했다고 가정해 보겠습니다.
public static long 계승(int n) {
n * 계승(n - 1)을 반환합니다.
}
메서드가 무한히 실행되어 StackOverflowError가 발생합니다.
이 섹션에서 논의된 예는 자신을 호출하는 재귀 메서드를 보여줍니다. 이를 직접 재귀라고 합니다. 간접 재귀를 생성하는 것도 가능합니다. 이는 A 메서드가 B 메서드를 호출하고, 이 메서드가 A 메서드를 호출할 때 발생합니다. 재귀와 관련된 여러 가지 메서드가 더 있을 수도 있습니다. 예를 들어 A 메서드는 B 메서드를 호출하고, 이 메서드는 C 메서드를 호출하며, 이 메서드는 A
메서드를 호출합니다.위 내용은 사례 연구: 계승 계산의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!