동적 프로그래밍을 사용하여 피보나치 수 찾기

이 섹션에서는 동적 프로그래밍을 사용하여 피보나치 수를 찾는 효율적인 알고리즘을 분석하고 설계합니다. 섹션 18.3, 사례 연구: 피보나치 수 계산에서는 다음과 같이 피보나치 수를 찾는 재귀적 방법을 제공합니다.

/**피보나치 수를 찾는 방법*/
공개 정적 긴 fib(긴 인덱스) {
if (index == 0) // 기본 사례
0을 반환합니다;
else if (index == 1) // 기본 사례
1을 반환;
else // 축소 및 재귀 호출
return fib(인덱스 - 1) + fib(인덱스 - 2);
}

이제 이 알고리즘의 복잡도가 O(2^n)임을 증명할 수 있습니다. 편의상 인덱스를 n이라고 하겠습니다. T(n)은 fib(n)을 찾는 알고리즘의 복잡도를 나타내고 c는 인덱스를 0 및 1과 비교하는 상수 시간을 나타냅니다. 즉, T(1)과 T(0)은 c입니다. 그리하여

하노이탑 문제의 분석과 유사하게 T(n)은 O(2^n)임을 알 수 있습니다.

그러나 이 알고리즘은 효율적이지 않습니다. 피보나치 수를 찾는 효율적인 알고리즘이 있습니까? 재귀 fib 메서드의 문제점은 해당 메서드가 동일한 인수로 중복 호출된다는 것입니다. 예를 들어 fib(4)을 계산하려면 fib(3) 및 fib(2)이 호출됩니다. fib(3)을 계산하려면 fib(2) 및 fib(1)이 호출됩니다. fib(2)이 중복 호출된다는 점에 유의하세요. 동일한 인수로 fib 메서드를 반복적으로 호출하지 않음으로써 이를 개선할 수 있습니다. 새로운 피보나치 수열은 이전 두 수를 시퀀스에 더하여 얻어집니다. 두 개의 변수 f0 및 f1을 사용하여 앞의 두 숫자를 저장하는 경우 f2를 추가하면 새 숫자 f2를 즉시 얻을 수 있습니다. f1과 함께. 이제 f1을 f0에 할당하고 f2를 f1에 할당하여 f0 및 f1을 업데이트해야 합니다.

아래 그림과 같습니다.

아래 코드에는 새로운 메소드가 구현되어 있습니다.

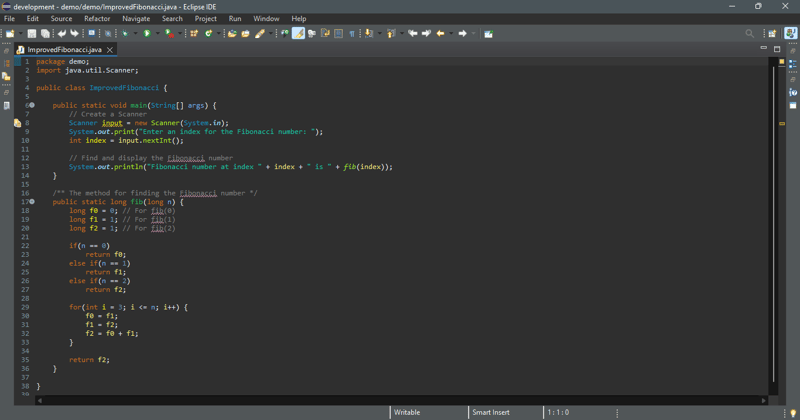
피보나치 수의 인덱스를 입력하세요: 6

인덱스 6의 피보나치 수는 8입니다

피보나치 수의 인덱스를 입력하세요: 7

인덱스 7의 피보나치 수는 13입니다

분명히 이 새로운 알고리즘의 복잡성은 O(n)입니다. 이는 재귀 O(2^n) 알고리즘에 비해 엄청난 개선입니다.

여기에 제시된 피보나치 수 계산 알고리즘은 동적 프로그래밍

이라는 접근 방식을 사용합니다. 동적 프로그래밍은 하위 문제를 해결한 다음 하위 문제의 솔루션을 결합하여 전체 솔루션을 얻는 프로세스입니다. 이는 자연스럽게 재귀적인 솔루션으로 이어집니다. 그러나 재귀를 사용하는 것은 하위 문제가 겹치기 때문에 비효율적입니다. 동적 프로그래밍의 핵심 아이디어는 하위 문제의 중복 계산을 피하기 위해 각 하위 문제를 한 번만 풀고 나중에 사용할 수 있도록 하위 문제의 결과를 저장하는 것입니다.

위 내용은 동적 프로그래밍을 사용하여 피보나치 수 찾기의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!