Javascript를 사용한 알고리즘을 통한 항해 - 버블 정렬-JS 튜토리얼-php.cn

버블 정렬이란 무엇입니까?

버블 정렬은 컴퓨터 과학에서 가장 간단한 정렬 알고리즘 중 하나입니다. 반복할 때마다 작은 요소가 목록의 맨 위로 "버블링"되는 방식에서 이름이 붙여진 이 도구는 정렬 알고리즘의 기본을 가르치기 위한 훌륭한 도구입니다. 대규모 데이터세트에 가장 효율적이지는 않지만 단순성은 정렬 알고리즘의 작동 방식을 이해하는 데 훌륭한 출발점이 됩니다.

버블 정렬의 작동 방식

버블 정렬은 목록을 반복적으로 살펴보고, 인접한 요소를 비교하고, 순서가 잘못된 경우 교체하는 방식으로 작동합니다. 더 이상 교체가 필요하지 않을 때까지 이 프로세스가 반복되어 목록이 정렬되었음을 나타냅니다.

다음은 단계별 분석입니다.

배열의 첫 번째 요소부터 시작하세요.
다음 요소와 비교해 보세요.
첫 번째 요소가 두 번째 요소보다 크면 서로 바꿉니다.
다음 요소로 이동하고 배열의 끝에 도달할 때까지 2~3단계를 반복합니다.
교환이 이루어진 경우 처음부터 과정을 반복하세요.
전체 패스에서 스왑이 이루어지지 않은 경우 배열이 정렬됩니다.

이 과정을 시각화해 보겠습니다.

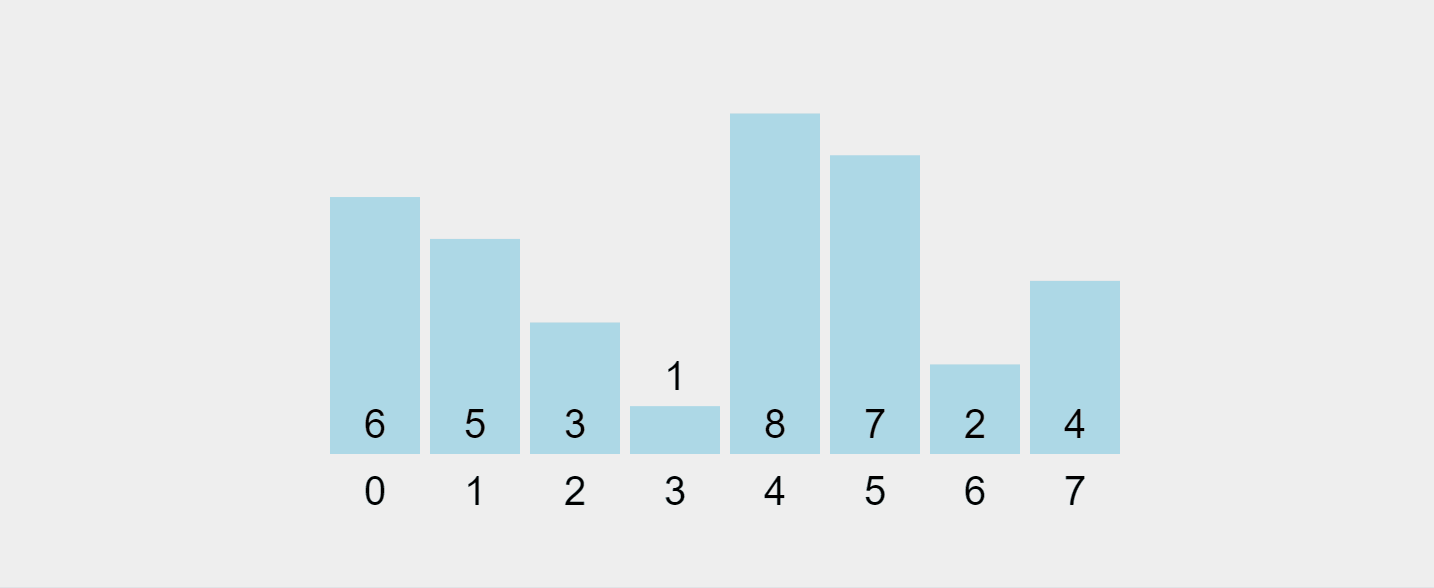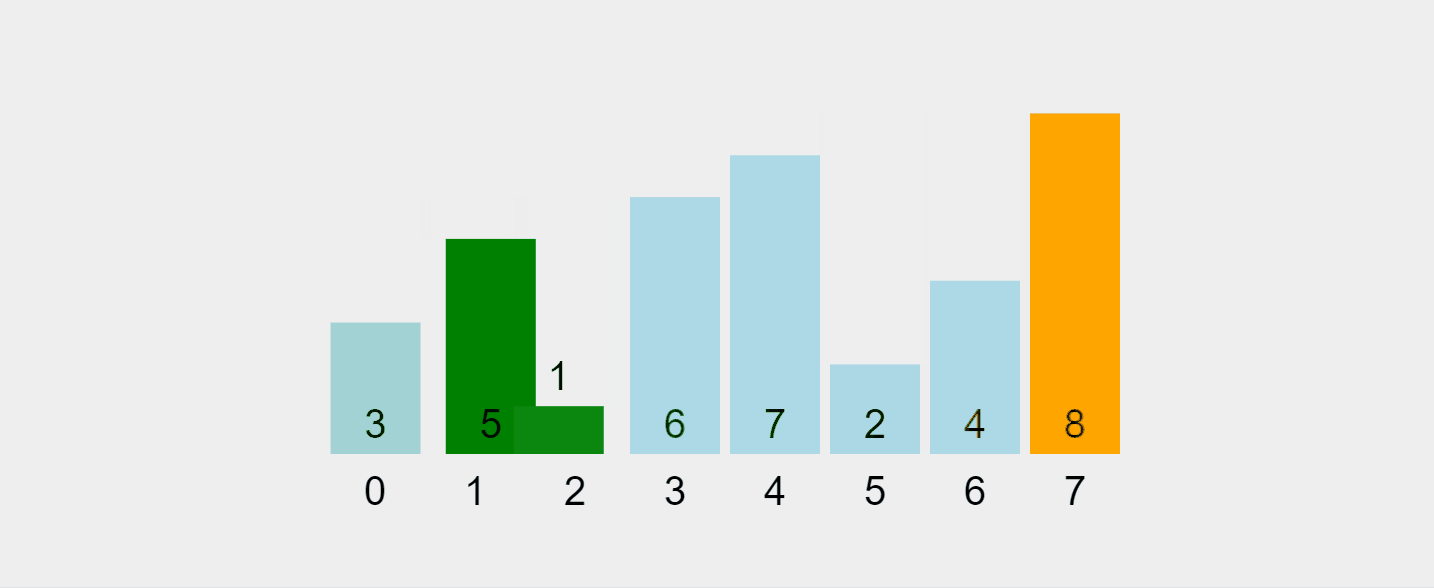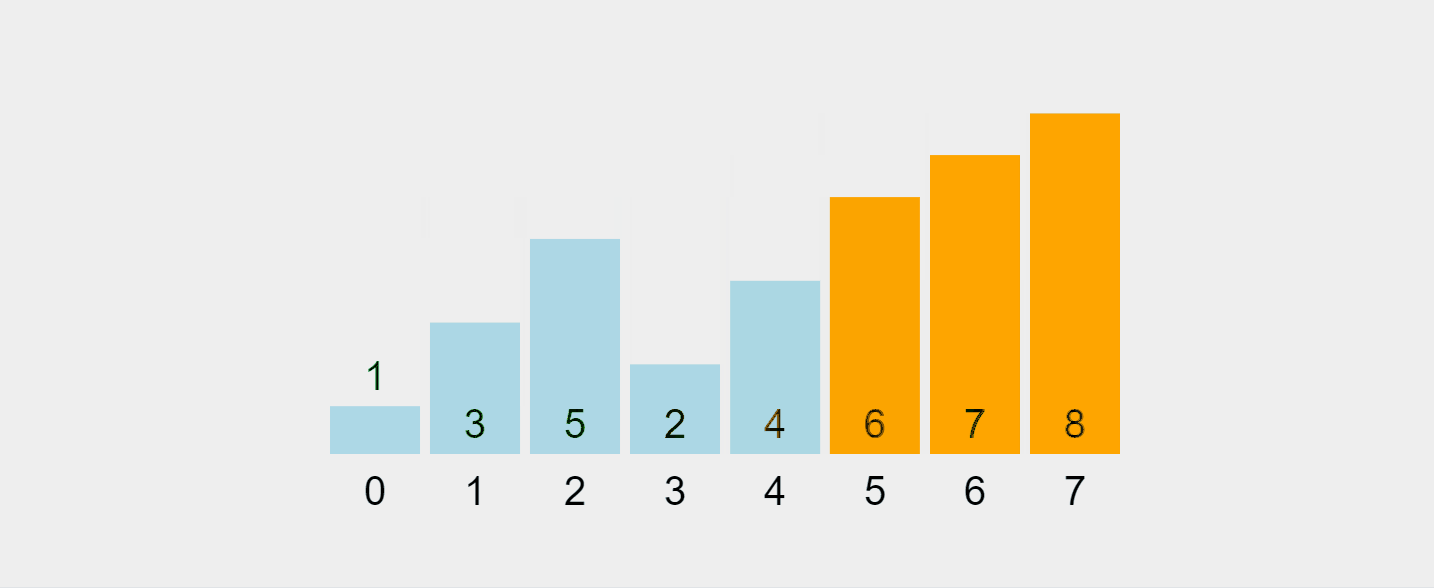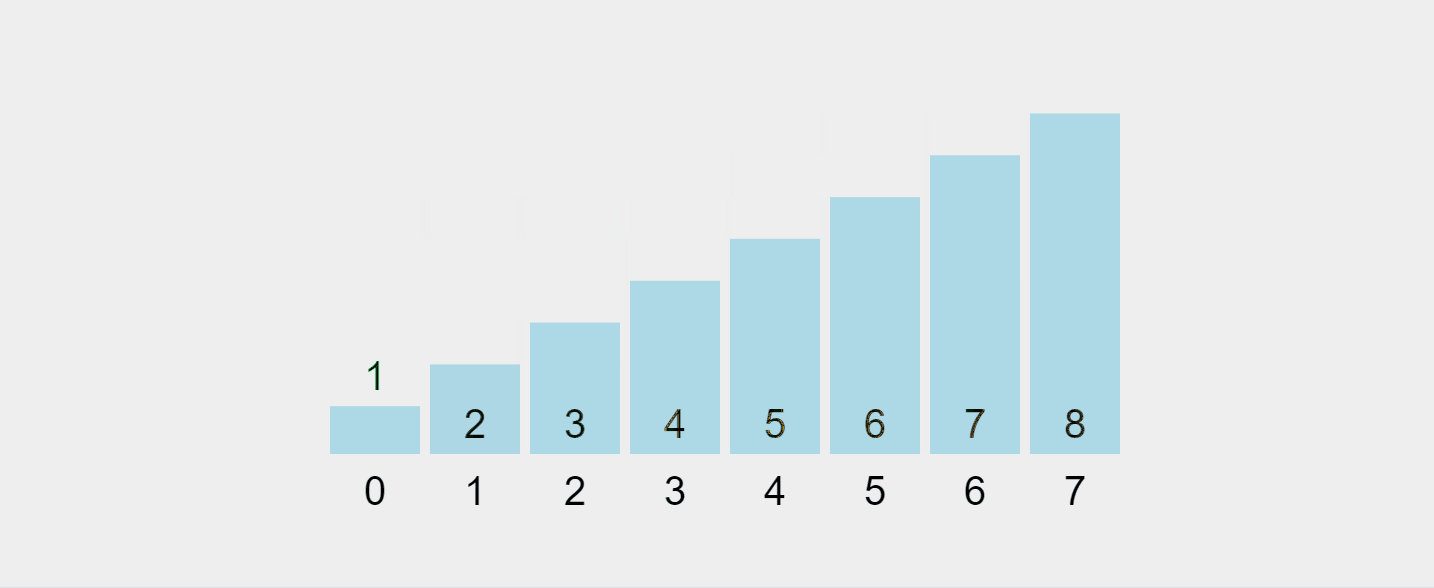
A Voyage through Algorithms using Javascript - Bubble Sort

https://visualgo.net/en/sorting에서 녹화한 gif

JavaScript에서 버블 정렬 구현

각각 최적화 수준이 증가하는 JavaScript의 세 가지 버블 정렬 구현을 살펴보겠습니다.

기본 구현(v1)

function bubbleSort(list) {
  // Outer loop: iterate through the entire list
  for (let i = 0; i < list.length - 1; i++) {
    // Inner loop: compare adjacent elements
    for (let j = 0; j < list.length - 1; j++) {
      // If the current element is greater than the next one
      if (list[j] > list[j + 1]) {
        // Swap the elements using destructuring assignment
        [list[j], list[j + 1]] = [list[j + 1], list[j]];
      }
    }
  }
  // Return the sorted list
  return list;
}

로그인 후 복사

이 기본 구현은 중첩 루프를 사용하여 인접한 요소를 비교하고 교환합니다. 외부 루프는 배열을 통해 충분한 패스를 수행하는 반면 내부 루프는 비교 및 교체를 수행합니다.

최적화된 구현(v2)

function bubbleSort(list) {
  // Outer loop: iterate through the entire list
  for (let i = 0; i < list.length - 1; i++) {
    // Flag to check if any swaps occurred in this pass
    let swapped = false;
    // Inner loop: compare adjacent elements
    for (let j = 0; j < list.length - 1; j++) {
      // If the current element is greater than the next one
      if (list[j] > list[j + 1]) {
        // Swap the elements using destructuring assignment
        [list[j], list[j + 1]] = [list[j + 1], list[j]];
        // Set the swapped flag to true
        swapped = true;
      }
    }    
    // If no swaps occurred in this pass, the list is sorted
    if (!swapped) {
      break; // Exit the outer loop early
    }
  }
  // Return the sorted list
  return list;
}

로그인 후 복사

이 버전에는 패스에서 스왑이 이루어졌는지 확인하기 위한 스왑 플래그가 도입되었습니다. 스왑이 발생하지 않으면 목록이 이미 정렬되어 있으므로 루프에서 조기에 벗어날 수 있습니다.

가장 최적화된 구현(v3)

function bubbleSort(list) {
  // Outer loop: iterate through the entire list
  for (let i = 0; i < list.length - 1; i++) {
    // Flag to check if any swaps occurred in this pass
    let swapped = false;
    // Inner loop: compare adjacent elements
    // Note: We reduce the upper bound by i in each pass
    for (let j = 0; j < list.length - 1 - i; j++) {
      // If the current element is greater than the next one
      if (list[j] > list[j + 1]) {
        // Swap the elements using destructuring assignment
        [list[j], list[j + 1]] = [list[j + 1], list[j]];
        // Set the swapped flag to true
        swapped = true;
      }
    }    
    // If no swaps occurred in this pass, the list is sorted
    if (!swapped) {
      break; // Exit the outer loop early
    }
  }
  // Return the sorted list
  return list;
}

로그인 후 복사

이 최종 최적화는 각 패스에서 내부 루프의 범위를 i만큼 줄입니다. 이는 각 패스 후에 정렬되지 않은 가장 큰 요소가 배열 끝의 올바른 위치로 "버블링"되기 때문입니다.

시간 및 공간 복잡도 분석

Bubble Sort의 성능 특성은 다음과 같습니다.

시간 복잡성:
- 최상의 사례: O(n) - 배열이 이미 정렬된 경우
- 평균 사례: O(n^2)
- 최악의 경우: O(n^2) - 배열이 역순인 경우
공간 복잡도: O(1) - 버블 정렬은 일정한 양의 추가 메모리만 필요로 하는 내부 정렬 알고리즘입니다.

빠른 정렬(평균 O(n log n)) 또는 병합 정렬(O(n log n))과 같은 고급 알고리즘과 비교할 때 Bubble Sort의 2차 시간 복잡도는 대규모 데이터 세트에 비효율적입니다.

버블 정렬의 장점과 단점

장점:

이해와 구현이 간단함
내부 정렬(O(1) 공백)
안정적인 정렬 알고리즘
이미 정렬된 목록을 감지할 수 있습니다

단점:

대규모 데이터세트에는 비효율적임(O(n^2))
거의 정렬된 데이터의 성능 저하
과도한 스와핑 작업

버블 정렬을 사용해야 하는 경우

교육 목적: 단순성으로 인해 기본 알고리즘 개념을 가르치는 데 탁월합니다.
소형 데이터 세트: 매우 작은 어레이의 경우 복잡한 알고리즘에 비해 성능 차이가 미미할 수 있습니다.
거의 정렬된 데이터: 최적화된 버전을 사용하면 거의 정렬된 목록에서 상당히 효율적일 수 있습니다.
제한된 메모리 환경: 내부 특성은 메모리가 극도로 제한된 시나리오에서 유리할 수 있습니다.

칵테일 정렬: 향상된 변형

칵테일 셰이크 정렬 또는 양방향 버블 정렬이라고도 하는 칵테일 정렬은 버블 정렬의 향상된 버전입니다. 목록을 양방향으로 탐색하여 요소를 올바른 위치로 보다 효율적으로 이동하는 데 도움이 됩니다.

How Cocktail Sort Works

Start with the first element and move towards the end, swapping adjacent elements if they're in the wrong order.
When you reach the end, start from the second-to-last element and move towards the beginning, again swapping elements as needed.
Repeat this process, narrowing the range of elements to check with each pass, until no swaps are needed.

Cocktail Sort is particularly useful in cases where the array has elements that are initially large at the beginning and small at the end, as it can reduce the total number of passes needed compared to traditional Bubble Sort.

Here's a visualization of Cocktail Sort:

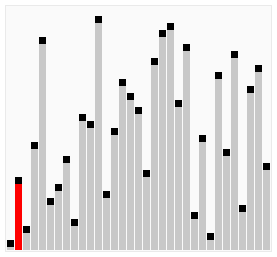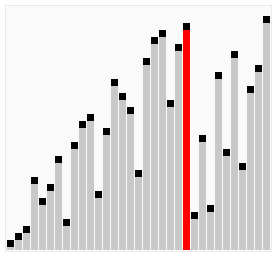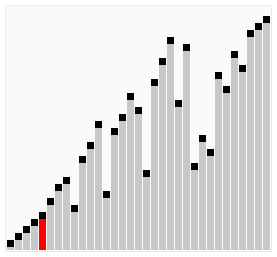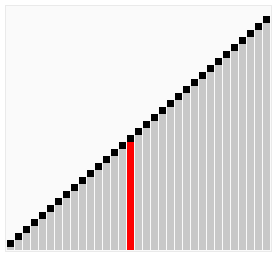
A Voyage through Algorithms using Javascript - Bubble Sort

Visual from Wikipedia: https://en.wikipedia.org/wiki/Cocktail_shaker_sort

Cocktail Sort implementation in Javascript

function cocktailSort(list) {
  let swapped;

  // The do...while loop ensures the sorting continues until no swaps are needed
  do {
    // Reset the swapped flag at the beginning of each complete iteration
    swapped = false;

    // First pass: left to right (like standard bubble sort)
    for (let i = 0; i < list.length - 1; i++) {
      // If the current element is greater than the next, swap them
      if (list[i] > list[i + 1]) {
        [list[i], list[i + 1]] = [list[i + 1], list[i]];
        // Mark that a swap occurred
        swapped = true;
      }
    }

    // If no swaps occurred in the first pass, the array is sorted
    if (!swapped) {
      break; // Exit the do...while loop early
    }

    // Reset the swapped flag for the second pass
    swapped = false;

    // Second pass: right to left (this is what makes it "cocktail" sort)
    for (let i = list.length - 2; i >= 0; i--) {
      // If the current element is greater than the next, swap them
      if (list[i] > list[i + 1]) {
        [list[i], list[i + 1]] = [list[i + 1], list[i]];
        // Mark that a swap occurred
        swapped = true;
      }
    }

    // The loop will continue if any swaps occurred in either pass
  } while (swapped);

  // Return the sorted list
  return list;
}

로그인 후 복사

This implementation alternates between forward and backward passes through the list, potentially reducing the number of iterations needed to sort the array.

Practical Applications and Use Cases

While Bubble Sort isn't typically used in production environments for large-scale applications, it can still find use in certain scenarios:

Educational tools: It's often used to introduce sorting algorithms and algorithm analysis in computer science education.
Embedded systems: In systems with very limited memory, its in-place sorting can be advantageous.
Small datasets: For sorting small lists (e.g., less than 50 elements), its simplicity might outweigh the performance benefits of more complex algorithms.
Nearly sorted data: If data is known to be almost sorted, an optimized Bubble Sort can be reasonably efficient.
Sorting stability requirement: When a stable sort is needed and simplicity is preferred over efficiency, Bubble Sort can be a straightforward choice.

Conclusion

Bubble Sort, despite its inefficiencies with large datasets, offers valuable insights into the world of sorting algorithms and algorithm analysis. Its straightforward approach makes it an excellent teaching tool for beginners in computer science.

Key takeaways are:

It's simple to understand and implement.
It has a time complexity of O(n^2), making it inefficient for large datasets.
It's an in-place and stable sorting algorithm.
Optimizations can improve its performance, especially for nearly sorted data.
It's primarily used for educational purposes and in scenarios with very small datasets or limited memory.

While you're unlikely to use Bubble Sort in production code for large-scale applications, the principles behind it are fundamental to many algorithms. The process of optimizing Bubble Sort teaches valuable lessons about algorithm improvement, serving as a stepping stone to more advanced computational problem-solving.

When it comes to algorithms, there's rarely a one-size-fits-all solution. The best algorithm for a given task depends on the specific requirements, constraints, and characteristics of your data. Bubble Sort, with all its limitations, still has its place in this diverse algorithmic ecosystem.

위 내용은 Javascript를 사용한 알고리즘을 통한 항해 - 버블 정렬의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!