설명 가능성의 궁극적인 질문은 첫 번째 설명이 무엇인가입니다. 20개의 CCF-A+ICLR 논문이 답변을 제공합니다.

AIxiv 칼럼은 본 사이트에서 학술 및 기술 콘텐츠를 게재하는 칼럼입니다. 지난 몇 년 동안 이 사이트의 AIxiv 칼럼에는 전 세계 주요 대학 및 기업의 최고 연구실을 대상으로 한 2,000개 이상의 보고서가 접수되어 학술 교류 및 보급을 효과적으로 촉진하고 있습니다. 공유하고 싶은 훌륭한 작품이 있다면 자유롭게 기여하거나 보고를 위해 연락주시기 바랍니다. 제출 이메일: liyazhou@jiqizhixin.com zhaoyunfeng@jiqizhixin.com
https://zhuanlan.zhihu.com/p/693747946
- 참조 1: https://zhuanlan.zhihu.com/p/369883667
- 참조 2: https://zhuanlan.zhihu.com/p/361686461
- 참조 3: https://zhuanlan.zhihu.com/p/704760363
- 4 참조: https://zhuanlan.zhihu.com/p/468569001
1번 보기: https://zhuanlan.zhihu.com/p/610774894 2번 보기: https://zhuanlan.zhihu.com/p/546433296
1.Junpeng Zhang, Qing Li, Liang Lin, Quanshi Zhang, "상호작용의 2단계 역학은 DNN의 과잉 맞춤 기능 학습의 시작점을 설명합니다", arXiv: 2405.10262 2.Qihan Ren, Yang Xu, Junpeng Zhang, Yue Xin, Dongrui Liu, Quanshi Zhang, arXiv의 "DNN 학습 상징적 상호 작용의 역학을 향하여":2407.19198

等效交互理论体系 [1] Huiqi Deng, Na Zou, Mengnan Du, Weifu Chen, Guocan Feng, Ziwei Yang, Zheyang Li, and Quanshi Zhang. Unifying Fourteen Post-Hoc Attribution Methods With Taylor Interactions. IEEE Transactions on Pattern Analysis and Machine Intelligence (IEEE T-PAMI), 2024. [2] Xu Cheng, Lei Cheng, Zhaoran Peng, Yang Xu, Tian Han, and Quanshi Zhang. Layerwise Change of Knowledge in Neural Networks. ICML, 2024. [3] Qihan Ren, Jiayang Gao, Wen Shen, and Quanshi Zhang. Where We Have Arrived in Proving the Emergence of Sparse Interaction Primitives in AI Models. ICLR, 2024. [4] Lu Chen, Siyu Lou, Benhao Huang, and Quanshi Zhang. Defining and Extracting Generalizable Interaction Primitives from DNNs. ICLR, 2024. [5] Huilin Zhou, Hao Zhang, Huiqi Deng, Dongrui Liu, Wen Shen, Shih-Han Chan, and Quanshi Zhang. Explaining Generalization Power of a DNN Using Interactive Concepts. AAAI, 2024. [6] Dongrui Liu, Huiqi Deng, Xu Cheng, Qihan Ren, Kangrui Wang, and Quanshi Zhang. Towards the Difficulty for a Deep Neural Network to Learn Concepts of Different Complexities. NeurIPS, 2023. [7] Quanshi Zhang, Jie Ren, Ge Huang, Ruiming Cao, Ying Nian Wu, and Song-Chun Zhu. Mining Interpretable AOG Representations from Convolutional Networks via Active Question Answering. IEEE Transactions on Pattern Analysis and Machine Intelligence (IEEE T-PAMI), 2020. [8] Xin Wang, Jie Ren, Shuyun Lin, Xiangming Zhu, Yisen Wang, and Quanshi Zhang. A Unified Approach to Interpreting and Boosting Adversarial Transferability. ICLR, 2021. [9] Hao Zhang, Sen Li, Yinchao Ma, Mingjie Li, Yichen Xie, and Quanshi Zhang. Interpreting and Boosting Dropout from a Game-Theoretic View. ICLR, 2021. [10] Mingjie Li, and Quanshi Zhang. Does a Neural Network Really Encode Symbolic Concept? ICML, 2023. [11] Lu Chen, Siyu Lou, Keyan Zhang, Jin Huang, and Quanshi Zhang. HarsanyiNet: Computing Accurate Shapley Values in a Single Forward Propagation. ICML, 2023. [12] Qihan Ren, Huiqi Deng, Yunuo Chen, Siyu Lou, and Quanshi Zhang. Bayesian Neural Networks Avoid Encoding Perturbation-Sensitive and Complex Concepts. ICML, 2023. [13] Jie Ren, Mingjie Li, Qirui Chen, Huiqi Deng, and Quanshi Zhang. Defining and Quantifying the Emergence of Sparse Concepts in DNNs. CVPR, 2023. [14] Jie Ren, Mingjie Li, Meng Zhou, Shih-Han Chan, and Quanshi Zhang. Towards Theoretical Analysis of Transformation Complexity of ReLU DNNs. ICML, 2022. [15] Jie Ren, Die Zhang, Yisen Wang, Lu Chen, Zhanpeng Zhou, Yiting Chen, Xu Cheng, Xin Wang, Meng Zhou, Jie Shi, and Quanshi Zhang. A Unified Game-Theoretic Interpretation of Adversarial Robustness. NeurIPS, 2021. [16] Wen Shen, Qihan Ren, Dongrui Liu, and Quanshi Zhang. Interpreting Representation Quality of DNNs for 3D Point Cloud Processing. NeurIPS, 2021. [17] Xin Wang, Shuyun Lin, Hao Zhang, Yufei Zhu, and Quanshi Zhang. Interpreting Attributions and Interactions of Adversarial Attacks. ICCV, 2021. [18] Wen Shen, Zhihua Wei, Shikun Huang, Binbin Zhang, Panyue Chen, Ping Zhao, and Quanshi Zhang. Verifiability and Predictability: Interpreting Utilities of Network Architectures for 3D Point Cloud Processing. CVPR, 2021. [19] Hao Zhang, Yichen Xie, Longjie Zheng, Die Zhang, and Quanshi Zhang. Interpreting Multivariate Shapley Interactions in DNNs. AAAI, 2021. [20] Die Zhang, Huilin Zhou, Hao Zhang, Xiaoyi Bao, Da Huo, Ruizhao Chen, Xu Cheng, Mengyue Wu, and Quanshi Zhang. Building Interpretable Interaction Trees for Deep NLP Models. AAAI, 2021.
샘플 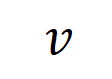
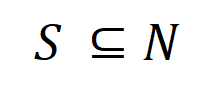 의 입력 변수 간의 "AND 관계"를 나타낸다고 생각할 수 있습니다. 예를 들어, 입력 문장
의 입력 변수 간의 "AND 관계"를 나타낸다고 생각할 수 있습니다. 예를 들어, 입력 문장 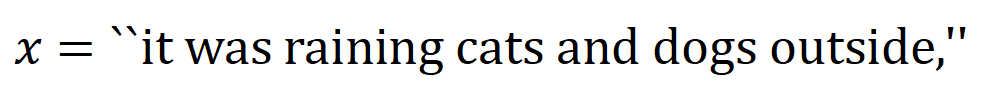 이 주어지면 신경망은
이 주어지면 신경망은 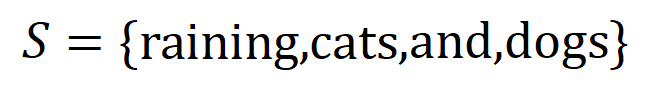 간의 상호 작용을 모델링하여
간의 상호 작용을 모델링하여 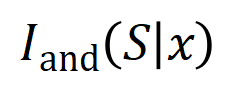 이 신경망의 출력 "폭우"를 유도하는 수치 유틸리티를 생성할 수 있습니다.
이 신경망의 출력 "폭우"를 유도하는 수치 유틸리티를 생성할 수 있습니다. 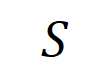 의 입력 변수가 가려지면 해당 수치 유틸리티가 신경망의 출력에서 제거됩니다. 마찬가지로 동등성 또는 상호 작용
의 입력 변수가 가려지면 해당 수치 유틸리티가 신경망의 출력에서 제거됩니다. 마찬가지로 동등성 또는 상호 작용 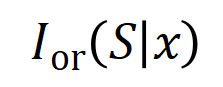 은 신경망으로 모델링된
은 신경망으로 모델링된  내의 입력 변수 간의 "OR 관계"를 나타냅니다. 예를 들어 입력 문장
내의 입력 변수 간의 "OR 관계"를 나타냅니다. 예를 들어 입력 문장 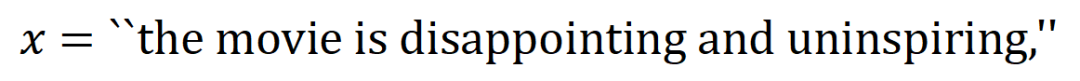 이 있을 때
이 있을 때 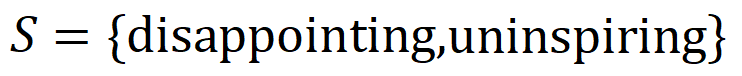 에 있는 단어가 나타나면 신경망의 출력을 구동하여 부정적인 감정을 분류합니다.
에 있는 단어가 나타나면 신경망의 출력을 구동하여 부정적인 감정을 분류합니다.
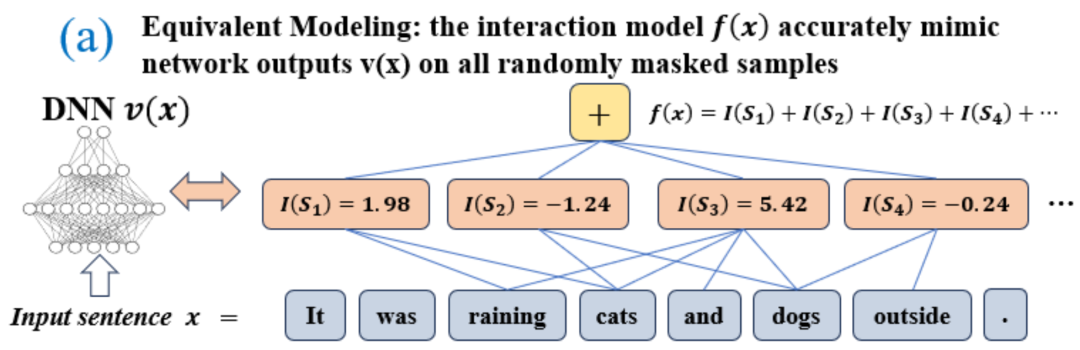
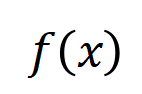 을 기반으로 하는 논리 모델을 통해 정확하게 맞출 수 있습니다. 각 상호 작용은 특정 입력 변수 세트(
을 기반으로 하는 논리 모델을 통해 정확하게 맞출 수 있습니다. 각 상호 작용은 특정 입력 변수 세트(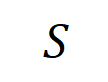 )를 모델링하는 신경망 간의 비선형 관계를 측정한 것입니다. 세트의 변수가 동시에 나타날 때만 트리거되고 상호 작용하며 출력
)를 모델링하는 신경망 간의 비선형 관계를 측정한 것입니다. 세트의 변수가 동시에 나타날 때만 트리거되고 상호 작용하며 출력 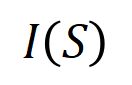 에 숫자 점수를 제공합니다. 세트의 변수
에 숫자 점수를 제공합니다. 세트의 변수  가 나타나면 트리거되거나 상호 작용합니다.
가 나타나면 트리거되거나 상호 작용합니다. 
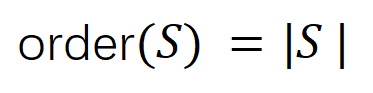
는 중요한 순서의 임계값을 나타냅니다. 상호 작용. 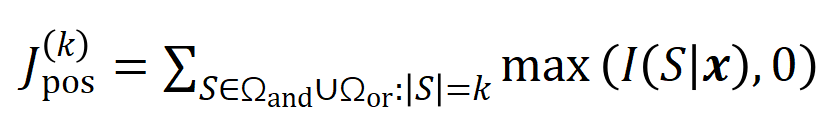
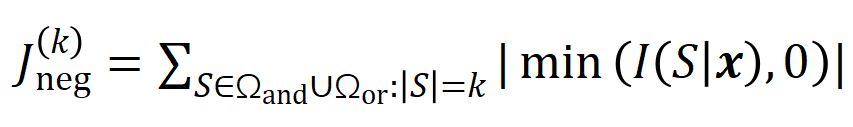
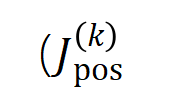 및
및 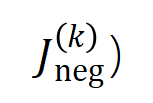 . 다양한 데이터 세트와 다양한 작업에 대해 훈련된 다양한 신경망의 훈련 프로세스에는 2단계 현상이 있습니다. 처음 두 개의 선택된 시점은 첫 번째 단계에 속하고 마지막 두 개의 시점은 두 번째 단계에 속합니다. 신경망 훈련 과정의 두 번째 단계에 들어간 직후, 테스트 손실과 신경망 훈련 손실 사이의 손실 격차가 크게 증가하기 시작합니다(마지막 열 참조). 이는 신경망 훈련의 2단계 현상이 모델 손실 격차의 변화에 맞춰 "정렬"된다는 것을 보여줍니다. 더 많은 실험 결과를 보려면 논문을 참조하세요.
. 다양한 데이터 세트와 다양한 작업에 대해 훈련된 다양한 신경망의 훈련 프로세스에는 2단계 현상이 있습니다. 처음 두 개의 선택된 시점은 첫 번째 단계에 속하고 마지막 두 개의 시점은 두 번째 단계에 속합니다. 신경망 훈련 과정의 두 번째 단계에 들어간 직후, 테스트 손실과 신경망 훈련 손실 사이의 손실 격차가 크게 증가하기 시작합니다(마지막 열 참조). 이는 신경망 훈련의 2단계 현상이 모델 손실 격차의 변화에 맞춰 "정렬"된다는 것을 보여줍니다. 더 많은 실험 결과를 보려면 논문을 참조하세요.
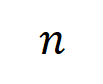 입력 변수를 포함하는 입력 샘플
입력 변수를 포함하는 입력 샘플  이 주어지면 입력 샘플
이 주어지면 입력 샘플  에서 추출된
에서 추출된  순 상호 작용을 벡터화
순 상호 작용을 벡터화 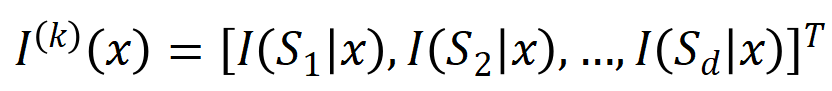 합니다. 여기서
합니다. 여기서 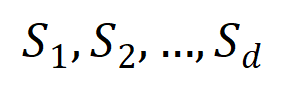 는
는 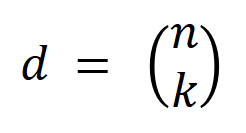
 순 상호 작용을 나타냅니다. 그런 다음 분류 작업에서 카테고리
순 상호 작용을 나타냅니다. 그런 다음 분류 작업에서 카테고리 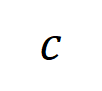 가 있는 모든 샘플에서 추출된 순서
가 있는 모든 샘플에서 추출된 순서  의 평균 상호 작용 벡터를 계산합니다. 여기서
의 평균 상호 작용 벡터를 계산합니다. 여기서 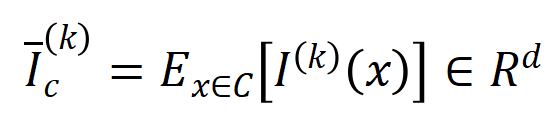 는 카테고리
는 카테고리 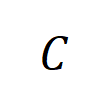 가 있는 샘플 집합을 나타냅니다.다음으로, 분류 작업에서 카테고리
가 있는 샘플 집합을 나타냅니다.다음으로, 분류 작업에서 카테고리 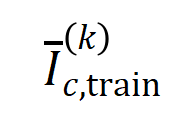 를 갖는 샘플의
를 갖는 샘플의  를 측정하기 위해 훈련 샘플에서 추출된 순서
를 측정하기 위해 훈련 샘플에서 추출된 순서 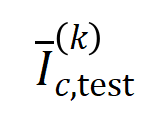 의 평균 상호 작용 벡터
의 평균 상호 작용 벡터  와 테스트 샘플에서 추출된 순서
와 테스트 샘플에서 추출된 순서  의 평균 상호 작용 벡터
의 평균 상호 작용 벡터 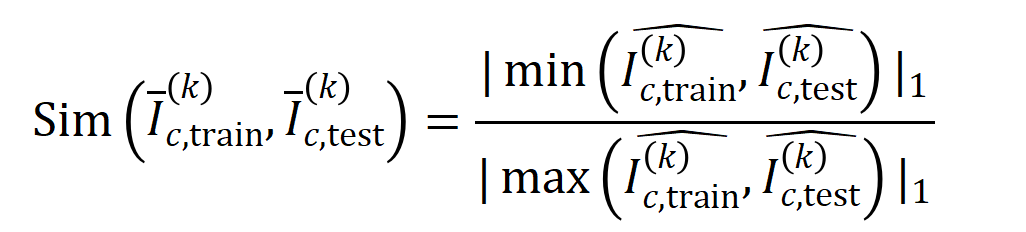
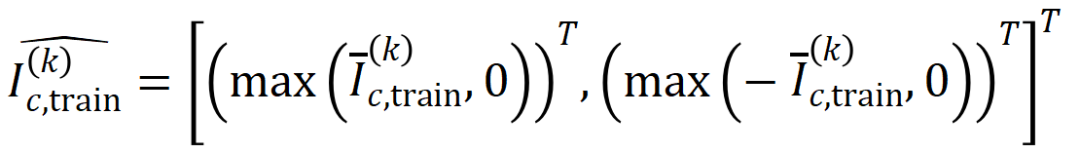 where,
where, 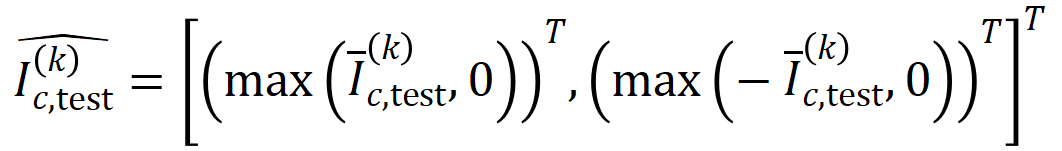 및
및 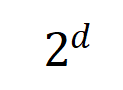 는 Jaccard 유사성을 계산하기 위해 두 개의
는 Jaccard 유사성을 계산하기 위해 두 개의 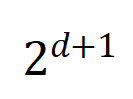 차원 상호 작용 벡터를 두 개의
차원 상호 작용 벡터를 두 개의 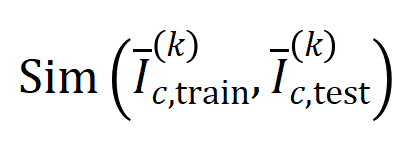 다양한 상호작용 순서를 계산하는 실험을 진행했습니다
다양한 상호작용 순서를 계산하는 실험을 진행했습니다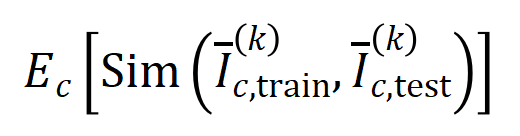 . 우리는 MNIST 데이터세트로 훈련된 LeNet, CIFAR-10 데이터세트로 훈련된 VGG-11, CUB200-2011 데이터세트로 훈련된 VGG-13, Tiny-ImageNet 데이터세트로 훈련된 AlexNet을 테스트했습니다. 계산 비용을 줄이기 위해 상위 10개 카테고리
. 우리는 MNIST 데이터세트로 훈련된 LeNet, CIFAR-10 데이터세트로 훈련된 VGG-11, CUB200-2011 데이터세트로 훈련된 VGG-13, Tiny-ImageNet 데이터세트로 훈련된 AlexNet을 테스트했습니다. 계산 비용을 줄이기 위해 상위 10개 카테고리
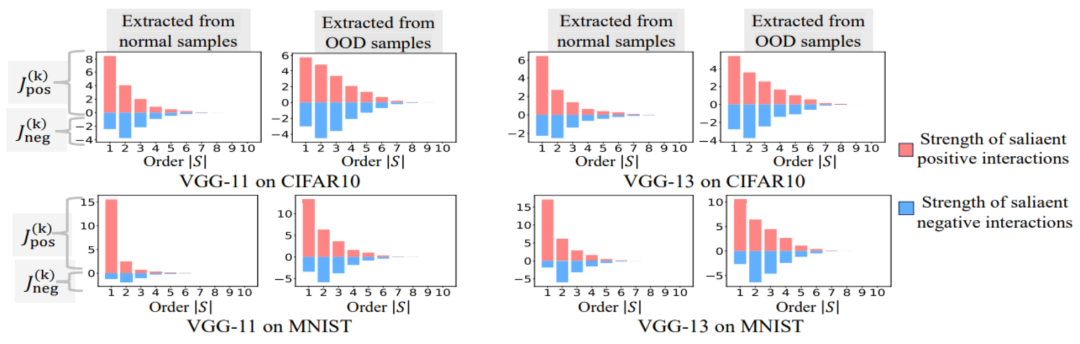
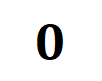 ,方差为
,方差为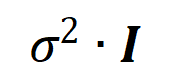 的正态分布。在上述假设下,我们能够证明初始化的神经网络建模的交互的强度和的分布呈现 “纺锤形”,即很少建模高阶和低阶交互,主要建模中阶交互。
的正态分布。在上述假设下,我们能够证明初始化的神经网络建模的交互的强度和的分布呈现 “纺锤形”,即很少建模高阶和低阶交互,主要建模中阶交互。
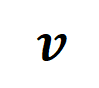 在特定样本上的 inference 改写为不同交互触发函数的加权和:
在特定样本上的 inference 改写为不同交互触发函数的加权和: 其中,
其中, 为标量权重,满足
为标量权重,满足 。而函数
。而函数 为交互触发函数,在任意一个遮挡样本
为交互触发函数,在任意一个遮挡样本 上都满足
上都满足 。函数
。函数 的具体形式可以由泰勒展开推导得到,可参考论文,这里不做赘述。
的具体形式可以由泰勒展开推导得到,可参考论文,这里不做赘述。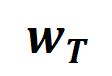 的学习。进一步地,实验室的前期工作 [3] 发现在同一任务上充分训练的不同的神经网络往往会建模相似的交互,所以我们可以将神经网络的学习看成是对一系列潜在的 ground truth 交互的拟合。由此,神经网络在训练到收敛时建模的交互可以看成是最小化下面的目标函数时得到的解:
的学习。进一步地,实验室的前期工作 [3] 发现在同一任务上充分训练的不同的神经网络往往会建模相似的交互,所以我们可以将神经网络的学习看成是对一系列潜在的 ground truth 交互的拟合。由此,神经网络在训练到收敛时建模的交互可以看成是最小化下面的目标函数时得到的解: 其中
其中 表示神经网络需要拟合的一系列潜在的 ground truth 交互。
表示神经网络需要拟合的一系列潜在的 ground truth 交互。 和
和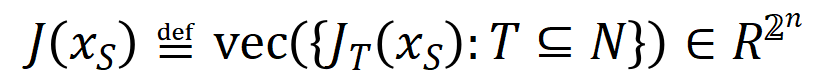 则分别表示将所有权重拼起来得到的向量和将所有交互触发函数的值拼起来得到的向量。
则分别表示将所有权重拼起来得到的向量和将所有交互触发函数的值拼起来得到的向量。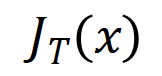 上的噪声,且该噪声随着交互阶数指数级增长 (在 [5] 中已有实验上的观察和验证) 。我们将有噪声下的神经网络的学习建模如下:
上的噪声,且该噪声随着交互阶数指数级增长 (在 [5] 中已有实验上的观察和验证) 。我们将有噪声下的神经网络的学习建模如下:
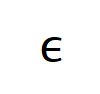 满足
满足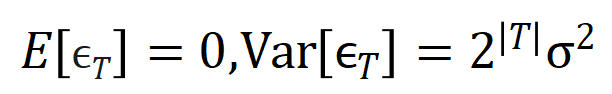 。且随着训练进行,噪声的方差
。且随着训练进行,噪声的方差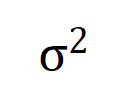 逐渐变小。
逐渐变小。 的情况下最小化上述损失函数,可得到最优交互权重
的情况下最小化上述损失函数,可得到最优交互权重 的解析解,如下图中的定理所示。
的解析解,如下图中的定理所示。
 变小),中低阶交互强度和高阶交互强度的比值逐渐减小(如下面的定理所示)。这解释了训练的第二阶段中神经网络逐渐学到更加高阶的交互的现象。
变小),中低阶交互强度和高阶交互强度的比值逐渐减小(如下面的定理所示)。这解释了训练的第二阶段中神经网络逐渐学到更加高阶的交互的现象。
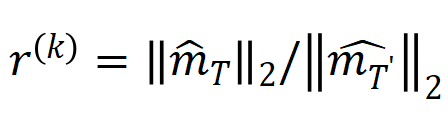 ,其中
,其中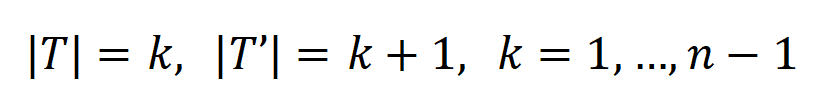 , 可以用来近似测量第 k 阶交互和第 k+1 阶交互强度的比值。在下图中,我们可以发现,在不同的输入单元个数 n 和不同的阶数 k 下,该比值都会随着
, 可以用来近似测量第 k 阶交互和第 k+1 阶交互强度的比值。在下图中,我们可以发现,在不同的输入单元个数 n 和不同的阶数 k 下,该比值都会随着 的减小而逐渐减小。
的减小而逐渐减小。
 的减小而逐渐减小。这说明随着训练进行(即
的减小而逐渐减小。这说明随着训练进行(即 逐渐变小),低阶交互强度与高阶交互强度的比值逐渐变小,神经网络逐渐学到更加高阶的交互。
逐渐变小),低阶交互强度与高阶交互强度的比值逐渐变小,神经网络逐渐学到更加高阶的交互。 下的理论交互值
下的理论交互值 在各个阶数上的分布
在各个阶数上的分布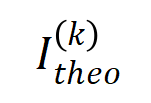 和实际训练过程中各阶交互的分布
和实际训练过程中各阶交互的分布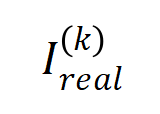 ,发现理论交互分布可以很好地预测实际训练中各时间点的交互强度分布。
,发现理论交互分布可以很好地预测实际训练中各时间点的交互强度分布。
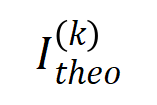 (蓝色直方图)和实际交互分布
(蓝色直方图)和实际交互分布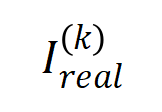 (橙色直方图)。在训练第二阶段的不同时间点,理论交互分布都可以很好地预测和匹配实际交互的分布。更多结果请参见论文。
(橙色直方图)。在训练第二阶段的不同时间点,理论交互分布都可以很好地预测和匹配实际交互的分布。更多结果请参见论文。 的最优解在噪声
的最优解在噪声 逐渐减小时的变化,那么第一阶段就可认为是交互从初始化的随机交互逐渐收敛到最优解的过程。
逐渐减小时的变化,那么第一阶段就可认为是交互从初始化的随机交互逐渐收敛到最优解的过程。
위 내용은 설명 가능성의 궁극적인 질문은 첫 번째 설명이 무엇인가입니다. 20개의 CCF-A+ICLR 논문이 답변을 제공합니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

Video Face Swap
완전히 무료인 AI 얼굴 교환 도구를 사용하여 모든 비디오의 얼굴을 쉽게 바꾸세요!

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)
 'Defect Spectrum'은 기존 결함 감지의 경계를 뛰어넘어 초고정밀 및 풍부한 의미론적 산업 결함 감지를 최초로 달성합니다.
Jul 26, 2024 pm 05:38 PM
'Defect Spectrum'은 기존 결함 감지의 경계를 뛰어넘어 초고정밀 및 풍부한 의미론적 산업 결함 감지를 최초로 달성합니다.
Jul 26, 2024 pm 05:38 PM
현대 제조업에서 정확한 결함 검출은 제품 품질을 보장하는 열쇠일 뿐만 아니라 생산 효율성을 향상시키는 핵심이기도 합니다. 그러나 기존 결함 감지 데이터세트는 실제 적용에 필요한 정확성과 의미론적 풍부함이 부족한 경우가 많아 모델이 특정 결함 카테고리나 위치를 식별할 수 없게 됩니다. 이 문제를 해결하기 위해 광저우 과학기술대학교와 Simou Technology로 구성된 최고 연구팀은 산업 결함에 대한 상세하고 의미론적으로 풍부한 대규모 주석을 제공하는 "DefectSpectrum" 데이터 세트를 혁신적으로 개발했습니다. 표 1에서 볼 수 있듯이, 다른 산업 데이터 세트와 비교하여 "DefectSpectrum" 데이터 세트는 가장 많은 결함 주석(5438개의 결함 샘플)과 가장 상세한 결함 분류(125개의 결함 카테고리)를 제공합니다.
 수백만 개의 결정 데이터로 훈련하여 결정학적 위상 문제를 해결하는 딥러닝 방법인 PhAI가 Science에 게재되었습니다.
Aug 08, 2024 pm 09:22 PM
수백만 개의 결정 데이터로 훈련하여 결정학적 위상 문제를 해결하는 딥러닝 방법인 PhAI가 Science에 게재되었습니다.
Aug 08, 2024 pm 09:22 PM
Editor |KX 오늘날까지 단순한 금속부터 큰 막 단백질에 이르기까지 결정학을 통해 결정되는 구조적 세부 사항과 정밀도는 다른 어떤 방법과도 비교할 수 없습니다. 그러나 가장 큰 과제인 소위 위상 문제는 실험적으로 결정된 진폭에서 위상 정보를 검색하는 것입니다. 덴마크 코펜하겐 대학의 연구원들은 결정 위상 문제를 해결하기 위해 PhAI라는 딥러닝 방법을 개발했습니다. 수백만 개의 인공 결정 구조와 그에 상응하는 합성 회절 데이터를 사용하여 훈련된 딥러닝 신경망은 정확한 전자 밀도 맵을 생성할 수 있습니다. 연구는 이 딥러닝 기반의 순순한 구조 솔루션 방법이 단 2옹스트롬의 해상도로 위상 문제를 해결할 수 있음을 보여줍니다. 이는 원자 해상도에서 사용할 수 있는 데이터의 10~20%에 해당하는 반면, 기존의 순순한 계산은
 NVIDIA 대화 모델 ChatQA는 버전 2.0으로 발전했으며 컨텍스트 길이는 128K로 언급되었습니다.
Jul 26, 2024 am 08:40 AM
NVIDIA 대화 모델 ChatQA는 버전 2.0으로 발전했으며 컨텍스트 길이는 128K로 언급되었습니다.
Jul 26, 2024 am 08:40 AM
오픈 LLM 커뮤니티는 백개의 꽃이 피어 경쟁하는 시대입니다. Llama-3-70B-Instruct, QWen2-72B-Instruct, Nemotron-4-340B-Instruct, Mixtral-8x22BInstruct-v0.1 등을 보실 수 있습니다. 훌륭한 연기자. 그러나 GPT-4-Turbo로 대표되는 독점 대형 모델과 비교하면 개방형 모델은 여전히 많은 분야에서 상당한 격차를 보이고 있습니다. 일반 모델 외에도 프로그래밍 및 수학을 위한 DeepSeek-Coder-V2, 시각 언어 작업을 위한 InternVL과 같이 핵심 영역을 전문으로 하는 일부 개방형 모델이 개발되었습니다.
 Google AI가 IMO 수학 올림피아드 은메달을 획득하고 수학적 추론 모델 AlphaProof가 출시되었으며 강화 학습이 다시 시작되었습니다.
Jul 26, 2024 pm 02:40 PM
Google AI가 IMO 수학 올림피아드 은메달을 획득하고 수학적 추론 모델 AlphaProof가 출시되었으며 강화 학습이 다시 시작되었습니다.
Jul 26, 2024 pm 02:40 PM
AI의 경우 수학 올림피아드는 더 이상 문제가 되지 않습니다. 목요일에 Google DeepMind의 인공 지능은 AI를 사용하여 올해 국제 수학 올림피아드 IMO의 실제 문제를 해결하는 위업을 달성했으며 금메달 획득에 한 걸음 더 다가섰습니다. 지난 주 막 끝난 IMO 대회에는 대수학, 조합론, 기하학, 수론 등 6개 문제가 출제됐다. 구글이 제안한 하이브리드 AI 시스템은 4문제를 맞혀 28점을 얻어 은메달 수준에 이르렀다. 이달 초 UCLA 종신 교수인 테렌스 타오(Terence Tao)가 상금 100만 달러의 AI 수학 올림피아드(AIMO Progress Award)를 추진했는데, 예상외로 7월 이전에 AI 문제 해결 수준이 이 수준으로 향상됐다. IMO에서 동시에 질문을 해보세요. 가장 정확하게 하기 어려운 것이 IMO인데, 역사도 가장 길고, 규모도 가장 크며, 가장 부정적이기도 합니다.
 PRO | MoE 기반의 대형 모델이 더 주목받는 이유는 무엇인가요?
Aug 07, 2024 pm 07:08 PM
PRO | MoE 기반의 대형 모델이 더 주목받는 이유는 무엇인가요?
Aug 07, 2024 pm 07:08 PM
2023년에는 AI의 거의 모든 분야가 전례 없는 속도로 진화하고 있다. 동시에 AI는 구체화된 지능, 자율주행 등 핵심 트랙의 기술적 한계를 지속적으로 확장하고 있다. 멀티모달 추세 하에서 AI 대형 모델의 주류 아키텍처인 Transformer의 상황이 흔들릴까요? MoE(Mixed of Experts) 아키텍처를 기반으로 한 대형 모델 탐색이 업계에서 새로운 트렌드가 된 이유는 무엇입니까? 대형 비전 모델(LVM)이 일반 비전 분야에서 새로운 돌파구가 될 수 있습니까? ...지난 6개월 동안 공개된 본 사이트의 2023 PRO 회원 뉴스레터에서 위 분야의 기술 동향과 산업 변화에 대한 심층 분석을 제공하여 새로운 환경에서 귀하의 목표 달성에 도움이 되는 10가지 특별 해석을 선택했습니다. 년. 준비하세요. 이 해석은 2023년 50주차에 나온 것입니다.
 대형 모델에 대한 새로운 과학적이고 복잡한 질문 답변 벤치마크 및 평가 시스템을 제공하기 위해 UNSW, Argonne, University of Chicago 및 기타 기관이 공동으로 SciQAG 프레임워크를 출시했습니다.
Jul 25, 2024 am 06:42 AM
대형 모델에 대한 새로운 과학적이고 복잡한 질문 답변 벤치마크 및 평가 시스템을 제공하기 위해 UNSW, Argonne, University of Chicago 및 기타 기관이 공동으로 SciQAG 프레임워크를 출시했습니다.
Jul 25, 2024 am 06:42 AM
편집자 |ScienceAI 질문 응답(QA) 데이터 세트는 자연어 처리(NLP) 연구를 촉진하는 데 중요한 역할을 합니다. 고품질 QA 데이터 세트는 모델을 미세 조정하는 데 사용될 수 있을 뿐만 아니라 LLM(대형 언어 모델)의 기능, 특히 과학적 지식을 이해하고 추론하는 능력을 효과적으로 평가하는 데에도 사용할 수 있습니다. 현재 의학, 화학, 생물학 및 기타 분야를 포괄하는 과학적인 QA 데이터 세트가 많이 있지만 이러한 데이터 세트에는 여전히 몇 가지 단점이 있습니다. 첫째, 데이터 형식이 비교적 단순하고 대부분이 객관식 질문이므로 평가하기 쉽지만 모델의 답변 선택 범위가 제한되고 모델의 과학적 질문 답변 능력을 완전히 테스트할 수 없습니다. 이에 비해 개방형 Q&A는
 정확도는 60.8%에 달합니다. Transformer를 기반으로 한 Zhejiang University의 화학적 역합성 예측 모델은 Nature 저널에 게재되었습니다.
Aug 06, 2024 pm 07:34 PM
정확도는 60.8%에 달합니다. Transformer를 기반으로 한 Zhejiang University의 화학적 역합성 예측 모델은 Nature 저널에 게재되었습니다.
Aug 06, 2024 pm 07:34 PM
Editor | KX 역합성은 약물 발견 및 유기 합성에서 중요한 작업이며, 프로세스 속도를 높이기 위해 AI가 점점 더 많이 사용되고 있습니다. 기존 AI 방식은 성능이 만족스럽지 못하고 다양성이 제한적입니다. 실제로 화학 반응은 종종 반응물과 생성물 사이에 상당한 중복이 발생하는 국지적인 분자 변화를 일으킵니다. 이에 영감을 받아 Zhejiang University의 Hou Tingjun 팀은 단일 단계 역합성 예측을 분자 문자열 편집 작업으로 재정의하고 표적 분자 문자열을 반복적으로 정제하여 전구체 화합물을 생성할 것을 제안했습니다. 그리고 고품질의 다양한 예측이 가능한 편집 기반 역합성 모델 EditRetro를 제안합니다. 광범위한 실험을 통해 이 모델은 표준 벤치마크 데이터 세트 USPTO-50 K에서 60.8%의 상위 1 정확도로 탁월한 성능을 달성하는 것으로 나타났습니다.
 자연의 관점: 의학 분야의 인공지능 테스트는 혼란에 빠졌습니다. 어떻게 해야 할까요?
Aug 22, 2024 pm 04:37 PM
자연의 관점: 의학 분야의 인공지능 테스트는 혼란에 빠졌습니다. 어떻게 해야 할까요?
Aug 22, 2024 pm 04:37 PM
Editor | ScienceAI 제한된 임상 데이터를 기반으로 수백 개의 의료 알고리즘이 승인되었습니다. 과학자들은 누가 도구를 테스트해야 하며 최선의 방법은 무엇인지에 대해 토론하고 있습니다. 데빈 싱(Devin Singh)은 응급실에서 오랜 시간 치료를 기다리던 중 심장마비를 겪는 소아환자를 목격했고, 이를 계기로 대기시간을 단축하기 위해 AI 적용을 모색하게 됐다. SickKids 응급실의 분류 데이터를 사용하여 Singh과 동료들은 잠재적인 진단을 제공하고 테스트를 권장하는 일련의 AI 모델을 구축했습니다. 한 연구에 따르면 이러한 모델은 의사 방문 속도를 22.3% 단축하여 의료 검사가 필요한 환자당 결과 처리 속도를 거의 3시간 단축할 수 있는 것으로 나타났습니다. 그러나 인공지능 알고리즘의 연구 성공은 이를 입증할 뿐이다.






