추측 샘플링이 대규모 언어 모델의 추론 정확도를 잃을까요?
Mitchell Stern과 다른 사람들은 2018년에 추측 샘플링의 프로토타입 개념을 제안했습니다. 이 접근 방식은 이후 Lookahead Decoding, REST, Medusa 및 EAGLE을 포함한 다양한 작업에 의해 더욱 개발되고 개선되었습니다. 여기서 추측 샘플링은 LLM(대형 언어 모델)의 추론 프로세스 속도를 크게 향상시킵니다.
중요한 질문은 LLM의 추측 샘플링이 원래 모델의 정확성을 손상시키는가입니다. 대답부터 시작하겠습니다. 아니요.
표준 추측 샘플링 알고리즘은 무손실이며, 이 글에서는 수학적 분석과 실험을 통해 이를 증명할 것입니다.
수학적 증명
추측 샘플링 공식은 다음과 같이 정의할 수 있습니다.

여기서:
- ?은 균일 분포에서 샘플링된 실수입니다.
-
 은 예측할 다음 토큰입니다.
은 예측할 다음 토큰입니다. - ?(?)는 초안 모델에서 제공하는 다음 토큰 배포입니다.
- ?(?)는 기본 모델에서 제공하는 다음 토큰 배포입니다.
간단하게 하기 위해 확률 조건을 생략합니다. 실제로 ? 및 ?는 접두사 토큰 시퀀스  를 기반으로 하는 조건부 배포입니다.
를 기반으로 하는 조건부 배포입니다.
다음은 DeepMind 논문에 있는 이 공식의 무손실 증명입니다.

수학 방정식을 읽는 것이 너무 지루하다고 생각되면 다음으로 직관적인 다이어그램을 통해 증명 과정을 설명하겠습니다.
초안 모델 ?과 기본 모델 ?의 분포도입니다.
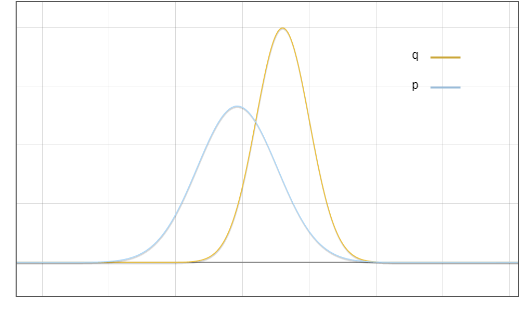
그림 1: 초안 모델 p와 기본 모델 q의 출력 분포의 확률 밀도 함수
주의해야 할 점 이것은 단지 이상적인 차트일 뿐입니다. 실제로 우리가 계산하는 것은 다음과 같은 이산 분포입니다.
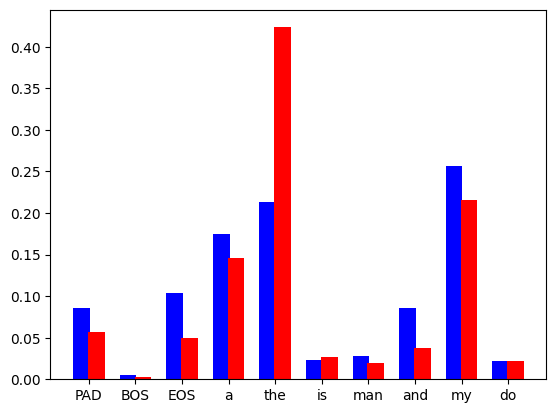
그림 2: 언어 모델은 어휘 세트에 있는 각 토큰의 이산 확률 분포를 예측하고 파란색 막대는 초안 모델에서 가져온 것입니다. 빨간색 막대는 기본 모델에서 가져온 것입니다.
그러나 단순성과 명확성을 위해 연속 근사법을 사용하여 이 문제를 논의합니다.
이제 질문은 분포 ? 에서 샘플링하지만 최종 결과는 ? 에서 샘플링한 것과 같기를 원한다는 것입니다. 핵심 아이디어는 빨간색 영역의 확률을 노란색 영역으로 이동하는 것입니다.
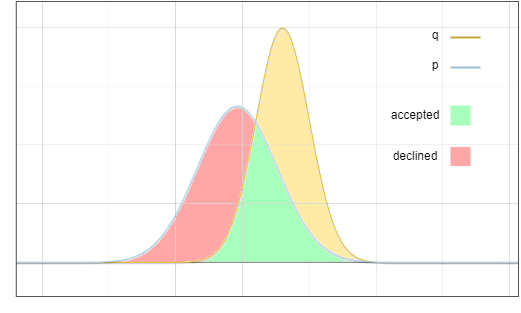
그림 3: 합격 및 거부 샘플링 영역
대상 분포 ? 두 부분의 합으로 볼 수 있습니다:
I. 수락
이 분기에는 두 가지 독립적인 이벤트가 있습니다.
- 초안 배포에 대한 샘플링은 특정 토큰을 생성합니까? 확률은 ?(?)
- 랜덤 변수 ? 토큰을 수락합니다. 확률은 다음과 같습니다.

다음 확률을 곱합니다. 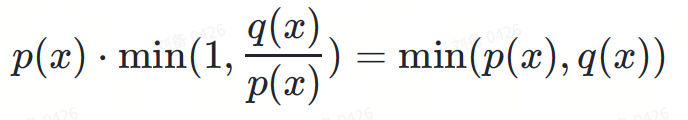
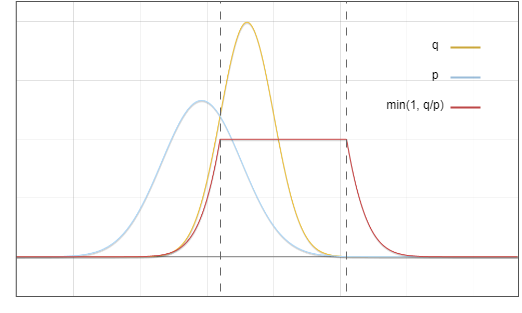
그림 4: 파란색 선과 빨간색 선을 곱하면 결과는 그림 6의 녹색 선이 됩니다.
II 이 분기에는 검증 거부
가 있습니다. 또한 두 개의 독립적인 이벤트:
- ?는 ?에서 특정 토큰을 거부합니다. 확률은 다음과 같습니다.

이것은 정수 값이며 이 값은 특정 토큰과 아무 관련이 없습니다. x
- 는 양수입니다. 분포 ?−?( 부분) 업샘플링은 특정 토큰을 생성합니까?, 확률은 다음과 같습니다:
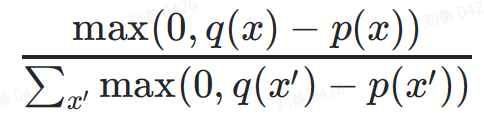
其分母作用是对概率分布进行归一化,以保持概率密度积分等于 1。
两项相乘,第二项的分母被约掉:
max(0,?(?)−?(?))
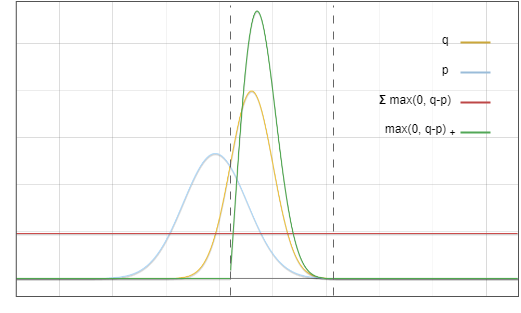
图5. 该图中的红线与绿线对应函数相乘,结果等于图6中的红线
为什么拒绝概率恰好可以归一化max(0,?−?) ?看起来似乎是巧合,这里一个重要的观察是,图 3 中红色区域的面积等于黄色区域的面积,因为所有概率密度函数的积分都等于 1。
将I, II两部分相加: 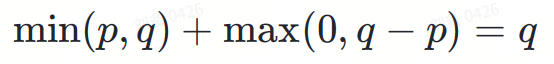
最后,我们得到了目标分布 ?。
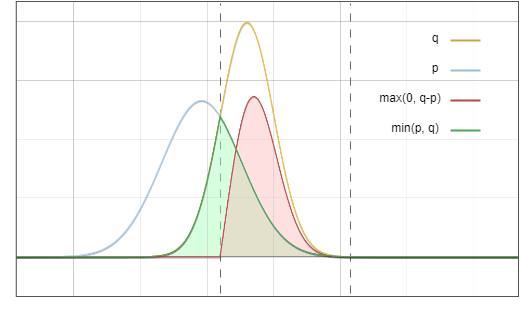
图6. 绿色区域与红色区域相加,正好等于黄线以下的面积
而这正是我们的目标。
实验
尽管我们已经从原理上证明了投机采样是无损的,但算法的实现仍然可能存在bug。因此,实验验证也是必要的。
我们对两种情况进行了实验:贪婪解码的确定性方法和多项式采样的随机方法。
贪婪解码
我们要求 LLM 生成两次短篇故事,首先使用普通推理,然后使用投机采样。两次采样温度均设置为 0。我们使用了 Medusa 中的投机采样实现。模型权重为 medusa-1.0-vicuna-7b-v1.5 及其基础模型 vicuna-7b-v1.5。
测试运行完成后,我们得到了两个精确相同的结果。生成的文本如下:
|
User: Please tell a tale about a cyperpunk knight named PPIO keeps a charming llama as his pet. Assistant: Once upon a time, in a world where technology had advanced beyond our wildest dreams, there lived a cyberpunk knight named PPIO. PPIO was a skilled warrior, with advanced cybernetic enhancements that gave him incredible strength and speed. He was also a man of great honor, always striving to do what was right and just. One day, while out on a mission, PPIO stumbled upon a beautiful llama. Despite being a cybernetic being, PPIO had a soft spot for animals and he couldn't resist rescuing the llama from whatever danger it may have been in. From that day on, the llama followed PPIO wherever he went, and the two became fast friends. The llama, whose name was Llama-ella, was a special llama. It had a unique ability to sense when someone was in danger and would let out a loud, distinctive call to alert them to the danger. PPIO was grateful for Llama-ella's ability and the two became an unstoppable team. Together, PPIO and Llama-ella took on all sorts of challenges, from battling cybernetic villains to rescuing innocent people from harm. They were a force to be reckoned with, and their bravery and honor were an inspiration to all who knew them. |
多项式采样
在随机采样的情况下,情况更加复杂。大多数在随机程序中重现结果的方法都使用固定的随机种子来利用伪随机生成器的确定性。但是,这种方法不适合我们的场景。我们的实验依赖于大数定律:如果有足够的样本,则实际分布与理论分布之间的误差将收敛于零。
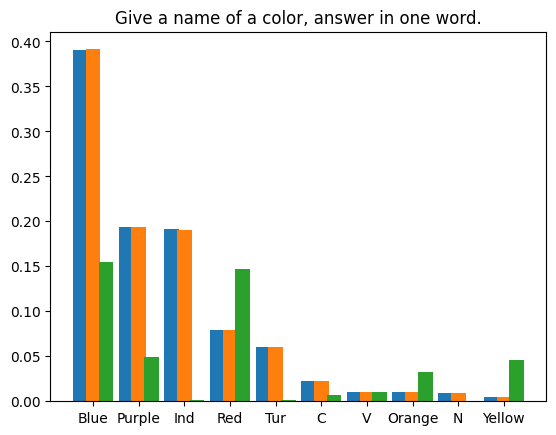
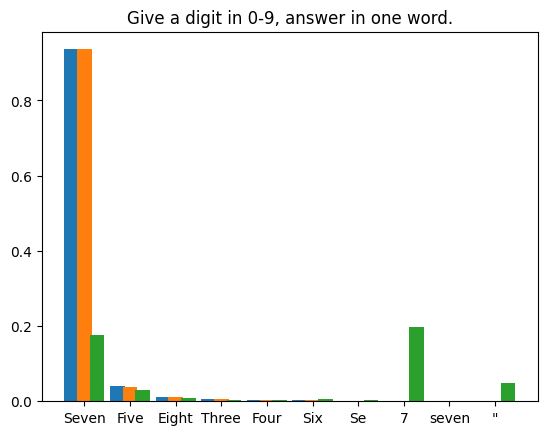
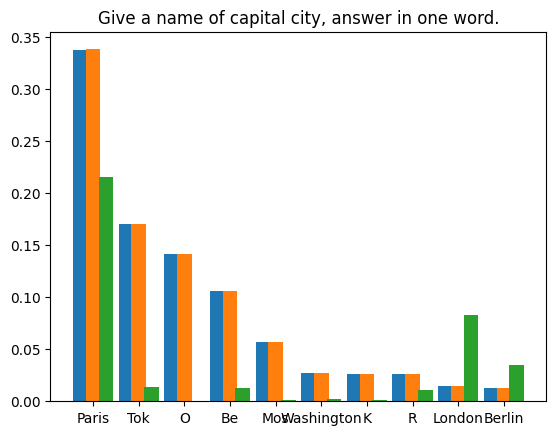
我们编制了四个提示文本,对LLM在每个提示下生成的首个token进行了 1,000,000 次投机采样迭代。使用的模型权重为 Llama3 8B Instruct 和 EAGLE-LLaMA3-Instruct-8B。统计结果如下所示:
|
|
|
Spekulatives Sampling schadet der Inferenzgenauigkeit großer Sprachmodelle nicht. Durch strenge mathematische Analysen und praktische Experimente demonstrieren wir die verlustfreie Natur des standardmäßigen spekulativen Stichprobenalgorithmus. Der mathematische Beweis zeigt, wie die spekulative Stichprobenformel die ursprüngliche Verteilung des zugrunde liegenden Modells bewahrt. Unsere Experimente, einschließlich deterministischer Greedy-Dekodierung und probabilistischer Polynomstichproben, bestätigen diese theoretischen Erkenntnisse weiter. Das Greedy-Decoding-Experiment lieferte mit und ohne spekulatives Sampling die gleichen Ergebnisse, während das Polynom-Sampling-Experiment zeigte, dass der Unterschied in der Token-Verteilung über eine große Anzahl von Stichproben hinweg vernachlässigbar ist.
|
위 내용은 추측 샘플링이 대규모 언어 모델의 추론 정확도를 잃을까요?의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

Video Face Swap
완전히 무료인 AI 얼굴 교환 도구를 사용하여 모든 비디오의 얼굴을 쉽게 바꾸세요!

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)
 ControlNet의 저자가 또 다른 히트를 쳤습니다! 이틀 만에 14,000개의 별을 획득하여 그림에서 그림을 생성하는 전체 과정
Jul 17, 2024 am 01:56 AM
ControlNet의 저자가 또 다른 히트를 쳤습니다! 이틀 만에 14,000개의 별을 획득하여 그림에서 그림을 생성하는 전체 과정
Jul 17, 2024 am 01:56 AM
역시 Tusheng 영상이지만 PaintsUndo는 다른 경로를 택했습니다. ControlNet 작성자 LvminZhang이 다시 살기 시작했습니다! 이번에는 회화 분야를 목표로 삼고 있습니다. 새로운 프로젝트인 PaintsUndo는 출시된 지 얼마 되지 않아 1.4kstar(여전히 상승세)를 받았습니다. 프로젝트 주소: https://github.com/lllyasviel/Paints-UNDO 이 프로젝트를 통해 사용자는 정적 이미지를 입력하고 PaintsUndo는 자동으로 라인 초안부터 완성품 따라가기까지 전체 페인팅 과정의 비디오를 생성하도록 도와줍니다. . 그리는 과정에서 선의 변화가 놀랍습니다. 최종 영상 결과는 원본 이미지와 매우 유사합니다. 완성된 그림을 살펴보겠습니다.
 RLHF에서 DPO, TDPO까지 대규모 모델 정렬 알고리즘은 이미 '토큰 수준'입니다.
Jun 24, 2024 pm 03:04 PM
RLHF에서 DPO, TDPO까지 대규모 모델 정렬 알고리즘은 이미 '토큰 수준'입니다.
Jun 24, 2024 pm 03:04 PM
AIxiv 칼럼은 본 사이트에서 학술 및 기술 콘텐츠를 게재하는 칼럼입니다. 지난 몇 년 동안 이 사이트의 AIxiv 칼럼에는 전 세계 주요 대학 및 기업의 최고 연구실을 대상으로 한 2,000개 이상의 보고서가 접수되어 학술 교류 및 보급을 효과적으로 촉진하고 있습니다. 공유하고 싶은 훌륭한 작품이 있다면 자유롭게 기여하거나 보고를 위해 연락주시기 바랍니다. 제출 이메일: liyazhou@jiqizhixin.com; zhaoyunfeng@jiqizhixin.com 인공 지능 개발 과정에서 LLM(대형 언어 모델)의 제어 및 안내는 항상 핵심 과제 중 하나였으며 이러한 모델이 두 가지 모두를 보장하는 것을 목표로 했습니다. 강력하고 안전하게 인간 사회에 봉사합니다. 인간 피드백(RL)을 통한 강화 학습 방법에 초점을 맞춘 초기 노력
 오픈 소스 AI 소프트웨어 엔지니어 목록의 1위인 UIUC의 에이전트 없는 솔루션은 SWE 벤치의 실제 프로그래밍 문제를 쉽게 해결합니다.
Jul 17, 2024 pm 10:02 PM
오픈 소스 AI 소프트웨어 엔지니어 목록의 1위인 UIUC의 에이전트 없는 솔루션은 SWE 벤치의 실제 프로그래밍 문제를 쉽게 해결합니다.
Jul 17, 2024 pm 10:02 PM
AIxiv 칼럼은 본 사이트에서 학술 및 기술 콘텐츠를 게재하는 칼럼입니다. 지난 몇 년 동안 이 사이트의 AIxiv 칼럼에는 전 세계 주요 대학 및 기업의 최고 연구실을 대상으로 한 2,000개 이상의 보고서가 접수되어 학술 교류 및 보급을 효과적으로 촉진하고 있습니다. 공유하고 싶은 훌륭한 작품이 있다면 자유롭게 기여하거나 보고를 위해 연락주시기 바랍니다. 제출 이메일: liyazhou@jiqizhixin.com; zhaoyunfeng@jiqizhixin.com 이 논문의 저자는 모두 일리노이 대학교 Urbana-Champaign(UIUC)의 Zhang Lingming 교사 팀 출신입니다. Steven Code Repair, 박사 4년차, 연구원
 arXiv 논문은 '연발'로 게시될 수 있습니다. Stanford alphaXiv 토론 플랫폼은 온라인이며 LeCun은 이를 좋아합니다.
Aug 01, 2024 pm 05:18 PM
arXiv 논문은 '연발'로 게시될 수 있습니다. Stanford alphaXiv 토론 플랫폼은 온라인이며 LeCun은 이를 좋아합니다.
Aug 01, 2024 pm 05:18 PM
건배! 종이 토론이 말로만 진행된다면 어떤가요? 최근 스탠포드 대학교 학생들은 arXiv 논문에 대한 질문과 의견을 직접 게시할 수 있는 arXiv 논문에 대한 공개 토론 포럼인 alphaXiv를 만들었습니다. 웹사이트 링크: https://alphaxiv.org/ 실제로 이 웹사이트를 특별히 방문할 필요는 없습니다. URL에서 arXiv를 alphaXiv로 변경하면 alphaXiv 포럼에서 해당 논문을 바로 열 수 있습니다. 논문, 문장: 오른쪽 토론 영역에서 사용자는 저자에게 논문의 아이디어와 세부 사항에 대해 질문하는 질문을 게시할 수 있습니다. 예를 들어 다음과 같이 논문 내용에 대해 의견을 제시할 수도 있습니다.
 리만 가설의 중요한 돌파구! 타오저쉬안(Tao Zhexuan)은 MIT와 옥스퍼드의 새로운 논문을 적극 추천했으며, 37세의 필즈상 수상자도 참여했다.
Aug 05, 2024 pm 03:32 PM
리만 가설의 중요한 돌파구! 타오저쉬안(Tao Zhexuan)은 MIT와 옥스퍼드의 새로운 논문을 적극 추천했으며, 37세의 필즈상 수상자도 참여했다.
Aug 05, 2024 pm 03:32 PM
최근 새천년 7대 과제 중 하나로 알려진 리만 가설이 새로운 돌파구를 마련했다. 리만 가설은 소수 분포의 정확한 특성과 관련된 수학에서 매우 중요한 미해결 문제입니다(소수는 1과 자기 자신으로만 나눌 수 있는 숫자이며 정수 이론에서 근본적인 역할을 합니다). 오늘날의 수학 문헌에는 리만 가설(또는 일반화된 형식)의 확립에 기초한 수학적 명제가 천 개가 넘습니다. 즉, 리만 가설과 그 일반화된 형식이 입증되면 천 개가 넘는 명제가 정리로 확립되어 수학 분야에 지대한 영향을 미칠 것이며, 리만 가설이 틀린 것으로 입증된다면, 이러한 제안의 일부도 그 효과를 잃을 것입니다. MIT 수학 교수 Larry Guth와 Oxford University의 새로운 돌파구
 OpenAI Super Alignment Team의 사후 작업: 두 개의 대형 모델이 게임을 하고 출력이 더 이해하기 쉬워졌습니다.
Jul 19, 2024 am 01:29 AM
OpenAI Super Alignment Team의 사후 작업: 두 개의 대형 모델이 게임을 하고 출력이 더 이해하기 쉬워졌습니다.
Jul 19, 2024 am 01:29 AM
AI 모델이 내놓은 답변이 전혀 이해하기 어렵다면 감히 사용해 보시겠습니까? 기계 학습 시스템이 더 중요한 영역에서 사용됨에 따라 우리가 그 결과를 신뢰할 수 있는 이유와 신뢰할 수 없는 경우를 보여주는 것이 점점 더 중요해지고 있습니다. 복잡한 시스템의 출력에 대한 신뢰를 얻는 한 가지 가능한 방법은 시스템이 인간이나 다른 신뢰할 수 있는 시스템이 읽을 수 있는 출력 해석을 생성하도록 요구하는 것입니다. 즉, 가능한 오류가 발생할 수 있는 지점까지 완전히 이해할 수 있습니다. 설립하다. 예를 들어, 사법 시스템에 대한 신뢰를 구축하기 위해 우리는 법원이 자신의 결정을 설명하고 뒷받침하는 명확하고 읽기 쉬운 서면 의견을 제공하도록 요구합니다. 대규모 언어 모델의 경우 유사한 접근 방식을 채택할 수도 있습니다. 그러나 이 접근 방식을 사용할 때는 언어 모델이 다음을 생성하는지 확인하세요.
 LLM은 시계열 예측에 적합하지 않습니다. 추론 능력도 사용하지 않습니다.
Jul 15, 2024 pm 03:59 PM
LLM은 시계열 예측에 적합하지 않습니다. 추론 능력도 사용하지 않습니다.
Jul 15, 2024 pm 03:59 PM
시계열 예측에 언어 모델을 실제로 사용할 수 있나요? Betteridge의 헤드라인 법칙(물음표로 끝나는 모든 뉴스 헤드라인은 "아니오"로 대답할 수 있음)에 따르면 대답은 아니오여야 합니다. 사실은 사실인 것 같습니다. 이렇게 강력한 LLM은 시계열 데이터를 잘 처리할 수 없습니다. 시계열, 즉 시계열은 이름에서 알 수 있듯이 시간 순서대로 배열된 데이터 포인트 시퀀스 집합을 나타냅니다. 시계열 분석은 질병 확산 예측, 소매 분석, 의료, 금융 등 다양한 분야에서 중요합니다. 시계열 분석 분야에서는 최근 많은 연구자들이 LLM(Large Language Model)을 사용하여 시계열의 이상 현상을 분류, 예측 및 탐지하는 방법을 연구하고 있습니다. 이 논문에서는 텍스트의 순차적 종속성을 잘 처리하는 언어 모델이 시계열로도 일반화될 수 있다고 가정합니다.
 최초의 Mamba 기반 MLLM이 출시되었습니다! 모델 가중치, 학습 코드 등은 모두 오픈 소스입니다.
Jul 17, 2024 am 02:46 AM
최초의 Mamba 기반 MLLM이 출시되었습니다! 모델 가중치, 학습 코드 등은 모두 오픈 소스입니다.
Jul 17, 2024 am 02:46 AM
AIxiv 칼럼은 본 사이트에서 학술 및 기술 콘텐츠를 게재하는 칼럼입니다. 지난 몇 년 동안 이 사이트의 AIxiv 칼럼에는 전 세계 주요 대학 및 기업의 최고 연구실을 대상으로 한 2,000개 이상의 보고서가 접수되어 학술 교류 및 보급을 효과적으로 촉진하고 있습니다. 공유하고 싶은 훌륭한 작품이 있다면 자유롭게 기여하거나 보고를 위해 연락주시기 바랍니다. 제출 이메일: liyazhou@jiqizhixin.com; zhaoyunfeng@jiqizhixin.com 서문 최근 몇 년 동안 다양한 분야에서 MLLM(Multimodal Large Language Model)의 적용이 눈에 띄는 성공을 거두었습니다. 그러나 많은 다운스트림 작업의 기본 모델로서 현재 MLLM은 잘 알려진 Transformer 네트워크로 구성됩니다.




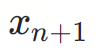 은 예측할 다음 토큰입니다.
은 예측할 다음 토큰입니다. 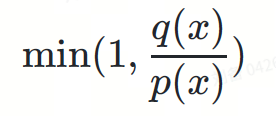
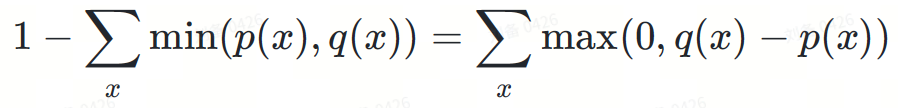
 Fazit
Fazit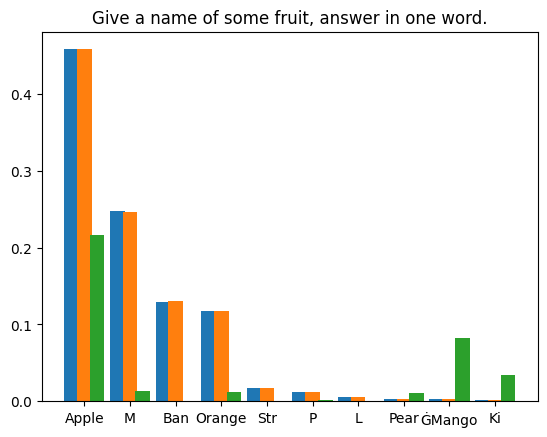 Zusammengenommen zeigen diese Ergebnisse, dass spekulative Stichproben die LLM-Inferenz ohne Einbußen bei der Genauigkeit erheblich beschleunigen können, was den Weg für effizientere und zugänglichere KI-Systeme in der Zukunft ebnet.
Zusammengenommen zeigen diese Ergebnisse, dass spekulative Stichproben die LLM-Inferenz ohne Einbußen bei der Genauigkeit erheblich beschleunigen können, was den Weg für effizientere und zugänglichere KI-Systeme in der Zukunft ebnet. 

