JavaScript의 재정적 정확성: 한 푼도 잃지 않고 돈을 처리하세요

빠르게 변화하는 금융 세계에서는 정확성이 가장 중요합니다. 반올림/정밀도 오류로 인해 백만 달러의 손실을 피하는 것이 항상 더 좋습니다.

돈에 관해서는 데이터 유형을 생각해 보세요.

이 글의 출발점은 돈이 바구니에 담긴 사과의 수를 세는 데 사용할 수 있는 평균적인 기본 숫자가 아니라는 깨달음입니다. 10€에 10$를 곱하면 무엇을 얻게 되나요? 힘들죠… 낡은 재킷 주머니에서 기적의 1,546달러를 발견한 적이 있나요? 네, 알아요. 이것도 실제로는 불가능합니다. 이러한 어리석은 예는 돈이 고유한 특정 규칙을 갖고 있으며 단순한 숫자로만 모델링할 수 없다는 사실을 설명하기 위해 여기에 있습니다. 나는 그것을 깨달은 최초의 사람이 아니라는 것을 확신합니다. (아마도 당신은 나보다 훨씬 먼저 그것을 깨달았을 것입니다). 2002년에 프로그래머 Martin Fowler는 Patterns of Enterprise Application Architecture에서 특정 속성과 피연산자 규칙을 사용하여 돈을 표현하는 방법을 제안했습니다. 그에게 돈 데이터 유형에 필요한 두 가지 최소한의 실행 가능한 속성은 다음과 같습니다.

amount
currency

이 매우 기본적인 표현은 단순하지만 강력한 화폐 모델을 구축하기 위한 출발점이 될 것입니다.

금액, 표현 방법

금액은 확실히 특정 숫자입니다. 고정된 정밀도를 갖습니다(다시 말하지만 주머니에 4.376$를 넣을 수는 없습니다). 이러한 제약을 존중하는 데 도움이 되는 표현 방법을 선택해야 합니다.

순진한 접근 방식, 기본 숫자 JavaScript 데이터 유형

스포일러 주의: 부동 소수점 숫자 표현의 어두운 세계에서 몇 센트(달러가 아닌 경우)가 사라지는 것을 보고 싶지 않다면 이는 확실히 좋은 생각이 아닙니다.

비용이 많이 드는 정밀도 오류

JavaScript 코딩 경험이 있다면 가장 간단한 계산이라도 처음에는 예상하지 못한 정밀도 오류가 발생할 수 있다는 것을 알고 계실 것입니다. 이 현상을 강조하는 가장 분명하고 잘 알려진 예는 다음과 같습니다.

0.1 + 0.2 !== 0.3 // true
0.1 + 0.2 // 0.30000000000000004

이 예가 완전히 이해되지 않는다면 JavaScript 기본 숫자 유형으로 작업할 때 발생할 수 있는 문제가 있는 모든 계산 결과에 대해 좀 더 자세히 설명하는 이 기사를 살펴보시기 바랍니다.

결과의 이 작은 델타는 사용자에게 무해한 것처럼 보일 수 있지만(약 10^-16 크기) 중요한 금융 애플리케이션에서는 이러한 오류가 빠르게 퍼질 수 있습니다. 각 거래에 유사한 계산이 포함되는 수천 개의 계좌 간에 자금을 이체하는 것을 고려해보세요. 약간의 부정확성이 더해지고, 당신이 그것을 알기도 전에 당신의 재무제표는 수천 달러의 손실을 입게 됩니다. 그리고 솔직히 말해서 돈과 관련하여 법적으로나 고객과 신뢰 관계를 구축하기 위해 오류가 허용되지 않는다는 데 우리 모두 동의할 수 있습니다.

왜 그런 오류가 발생합니까?

내 프로젝트 중 하나에서 문제가 발생했을 때 제가 스스로에게 던진 첫 번째 질문은 왜 ?입니다. 문제의 원인은 JavaScript가 아니며 이러한 부정확성은 다른 최신 프로그래밍 언어(Java, C, Python 등)에도 영향을 미친다는 것을 발견했습니다.

// In C
#include <stdio.h>

int main() {
    double a = 0.1;
    double b = 0.2;
    double sum = a + b;
    if (sum == 0.3) {
        printf("Equal\n");
    } else {
        printf("Not Equal\n"); // This block is executed
    }
    return 0;
}

// > Not equal

// In Java
public class doublePrecision {
    public static void main(String[] args) {

        double total = 0;
        total += 5.6;
        total += 5.8;
        System.out.println(total);
    }
}

// > 11.399999999999

사실 근본 원인은 부동 소수점 숫자를 표현하기 위해 이러한 언어에서 사용하는 표준, 즉 IEEE 754 표준에서 지정한 배정밀도(또는 단정밀도) 부동 소수점 형식에 있습니다.

IEEE 754 표준: 비트 표현 이야기

Javascript에서 기본 유형 숫자는 배정밀도 부동 소수점 숫자에 해당합니다. 즉, 숫자가 64비트로 인코딩되어 세 부분으로 나누어집니다.

• 기호용 1비트
• 지수 11비트
• 0부터 1까지의 가수(또는 분수)에 대한 52비트

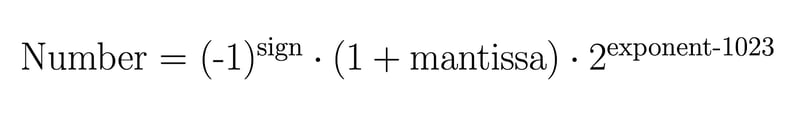
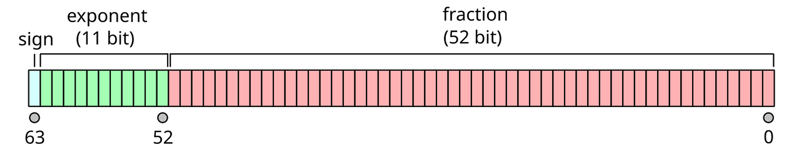
그런 다음 다음 공식을 사용하여 비트 표현을 10진수 값으로 변환해야 합니다.

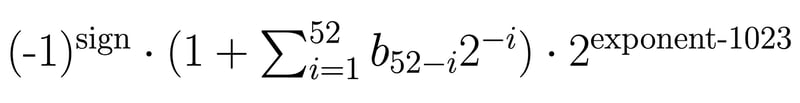
배정밀도 부동 소수점 숫자 표현의 예(약 1/3):

0 01111111101 0101010101010101010101010101010101010101010101010101

= (-1)^0 x (1 + 2^-2 + 2^-4 + 2^-6 + ... + 2^-50 + 2^-52) x 2^(1021-1023)
= 0.333333333333333314829616256247390992939472198486328125
~ 1/3

This format allows us to represent a vast range of values, but it can't represent every possible number with absolute precision (just between 0 and 1 you can find an infinity of numbers…). Many numbers cannot be represented exactly in binary form. To loop on the first example, that's the issue with 0.1 and 0.2. Double-point floating representation gives us an approximation of these value, so when you add these two imprecise representations, the result is also not exact.

A possible solution: Arbitrary Decimal Arithmetic

Now that you are fully convinced that handling money amounts with native JavaScript number type is a bad idea (at least I hope you begin to have doubts about it), the 1Billion$ question is how should you proceed ? A solution could be to make use of some of the powerful fixed-precision arithmetic packages available in JavaScript. For example Decimal.js (which is used by the popular ORM Prisma to represent its Decimal datatype) or Big.js.

These packages provide you with special datatypes that allow you to perform calculations with getting rid of precision errors we explained above.

// Example using Decimal.js
const Decimal = require('decimal.js');
const a = new Decimal('0.1');
const b = new Decimal('0.2');
const result = a.plus(b);

console.log(result.toString()); // Output: '0.3'

This approach provides you with another advantage, it drastically extends the maximum value that can be represented, which can become pretty handy when you are dealing with cryptocurrencies for example.
Even if it is really robust, that it not the one I prefer to choose to implement in my web applications. I find it easier and clearer to apply Stripe strategy to only deal with integer values.

Learn from Masters : Stripe, a No-Floating Points Strategy

We, at Theodo Fintech, value pragmatism! We love to take inspiration from the most succeeding companies in the industry. Stripe, the well-known billions$ company specialized in payment services, made the choice to handle money amounts without floating numbers but with integers. To do that, they use the smallest unit of the currency to represent a monetary amount.

// 10 USD are represented by
{
 "amount": 1000,
 "currency": "USD"
}

Currency Minimal Units… Are Not Consistent!

I guess that many of you already know this: all currencies don't have the smallest unit of the same magnitude. Most of them are "two-decimal" currencies (EUR, USD, GBP) which means that their smallest unit is 1/100th of the currency. However, some are "three-decimal" currencies (KWD) or even "zero-decimal" currencies (JPY). (You can find more information about it by following the ISO4217 standard). To handle these disparities, you should integrate to your money data representation the multiplicative factor to convert an amount represented in the smallest unit into the corresponding currency.

I Chose a Way to Represent Money Amount… OK, But Now, How Do I Round Them?

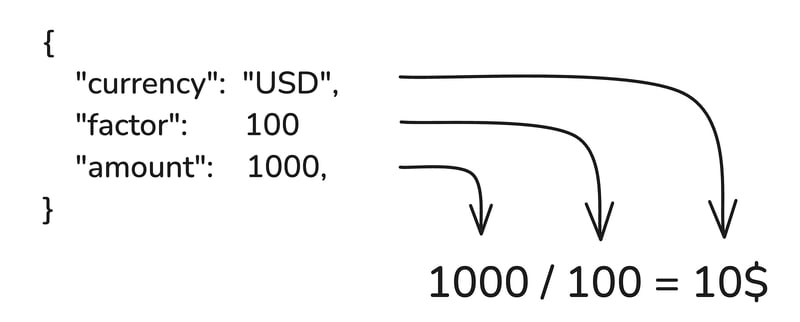
I guess you already figured it out, you can either work with native number , third party arbitrary-precision packages or integers, calculations can (and will) lead you to floating-point results that you will need to round to your monetary finite precision. As a quick example is never to much, let's say that you handle integer values and contracted a loan of 16k$ with a really precise interest rate of 8.5413% (ouch…). You then need to refund 16k$ plus an additional amount of

1600000 * 0.085413 // amount in cents
//Output in cents: 136660.8

The crux is to properly handle the rounding process of money amounts after calculations. Most of the time, you end up having to choose between three different kinds of rounding:

• Classic rounding: Round to the closest value and if halfway between two values, round up
• Banker rounding: Round to the closest value and if halfway between two values, round down if the number is even, and round up if the number is odd (this gives you numerical stability when you have to perform lots of rounding)
• Custom rounding: based on particular legislation for the currency you use and the use case you are handling

When it comes to roundings, there is not really any "magic sauce": you need to arbitrate depending on your situation. I recommend you always check legislation when you deal with a new currency and a new rounding use case (conversion, money split, interest rates for credits, …). You better follow regulations right away to avoid further troubles. For example, when it comes to conversion rates, most currencies have determined rules about needed precision and rounding rules (you can have a look at the EUR conversion rate rules here).

결론

이 글은 JavaScript로 금액을 처리할 수 있는 기존의 모든 가능성을 망라한 것이 아니며 완전한/완벽한 금액 데이터 모델을 제공하기 위한 것도 아닙니다. 저는 일관되고 회복력이 있으며 핀테크 업계의 주요 행위자들이 선택한 표현을 구현하기 위해 충분한 힌트와 지침을 제공하려고 노력했습니다. 주머니에 돈 한 푼도 잊지 않고 향후 프로젝트에서 금액 계산을 수행할 수 있기를 바랍니다(그렇지 않으면 오래된 재킷을 살펴보는 것을 잊지 마세요)!

위 내용은 JavaScript의 재정적 정확성: 한 푼도 잃지 않고 돈을 처리하세요의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!