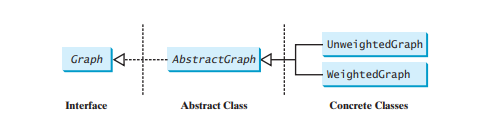
그래프 인터페이스는 그래프의 일반적인 작업을 정의합니다. Java 컬렉션 프레임워크는 복잡한 데이터 구조를 설계하는 좋은 예입니다. 데이터 구조의 공통 기능은 다음과 같이 인터페이스(예: Collection, Set, List, Queue)에 정의되어 있습니다. 그림 20.1. 추상 클래스(예: AbstractCollection, AbstractSet, AbstractList)는 부분적으로 인터페이스를 구현합니다. 구체적인 클래스(예: HashSet, LinkedHashSet, TreeSet, ArrayList, LinkedList, PriorityQueue) 구체적인 구현을 제공합니다. 이 디자인 패턴은 그래프 모델링에 유용합니다. 그래프의 모든 일반적인 작업을 포함하는 Graph라는 인터페이스와 Graph 인터페이스를 부분적으로 구현하는 AbstractGraph라는 추상 클래스를 정의하겠습니다. 디자인에 구체적인 그래프를 많이 추가할 수 있습니다. 예를 들어 UnweightedGraph 및 WeightedGraph라는 이름의 그래프를 정의하겠습니다. 이러한 인터페이스와 클래스의 관계는 아래 그림에 나와 있습니다.
그래프의 일반적인 작업은 무엇인가요? 일반적으로 그래프의 정점 수를 가져오고, 그래프의 모든 정점을 가져오고, 지정된 인덱스가 있는 정점 객체를 가져오고, 지정된 이름을 가진 정점의 인덱스를 가져오고, 정점에 대한 이웃을 가져와야 합니다. 정점의 차수, 그래프 지우기, 새 정점 추가, 새 간선 추가, 깊이 우선 검색 수행, 너비 우선 검색 수행. 깊이 우선 탐색과 너비 우선 탐색은 다음 섹션에서 소개하겠습니다. 아래 그림은 UML 다이어그램에서 이러한 방법을 보여줍니다.
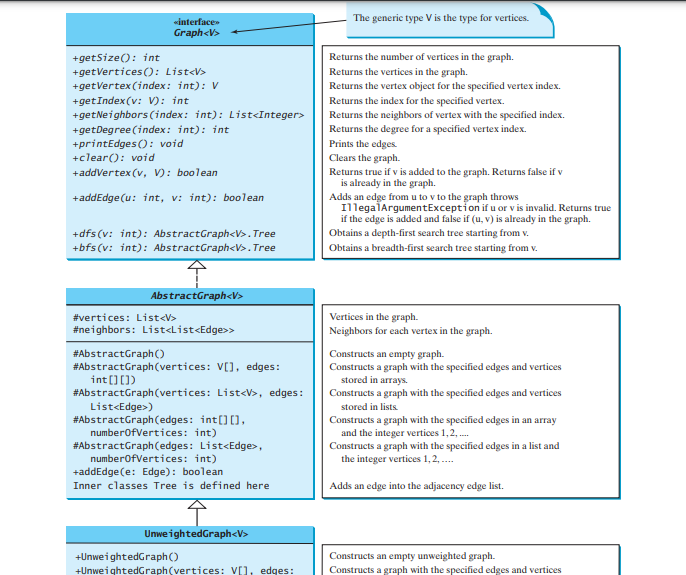
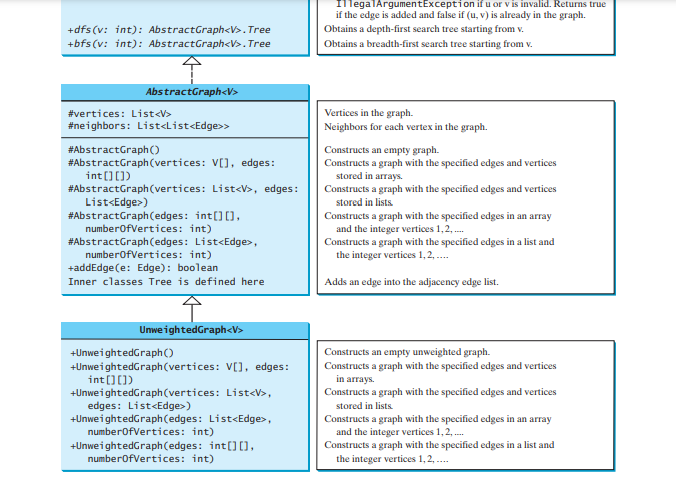
AbstractGraph는 새로운 방법을 도입하지 않습니다. 정점 목록과 가장자리 인접 목록은 AbstractGraph 클래스에 정의되어 있습니다. 이러한 데이터 필드를 사용하면 Graph 인터페이스에 정의된 모든 메소드를 구현하는 것으로 충분합니다. 편의상 그래프는 단순한 그래프라고 가정합니다. 즉, 정점 자체에는 가장자리가 없고 정점 u에서 v까지 평행한 가장자리도 없다고 가정합니다.
AbstractGraph는 Graph의 모든 메소드를 구현하며 를 추가하는 편리한 addEdge(edge) 메소드를 제외하고는 새로운 메소드를 도입하지 않습니다. >Edge 개체를 인접 가장자리 목록에 추가합니다. UnweightedGraph는 구체적인 Graph 인스턴스를 생성하기 위한 5개의 생성자를 사용하여 AbstractGraph
를 확장합니다.모든 유형의 꼭짓점을 사용하여 그래프를 만들 수 있습니다. 각 정점은 정점 목록의 정점 인덱스와 동일한 인덱스와 연결됩니다. 정점을 지정하지 않고 그래프를 생성하면 정점과 인덱스가 동일합니다.
AbstractGraph 클래스는 Graph 인터페이스의 모든 메소드를 구현합니다. 그렇다면 왜 추상적으로 정의됩니까? 앞으로는 AbstractGraph에서 구현할 수 없는 Graph 인터페이스에 새로운 메소드를 추가해야 할 수도 있습니다. 클래스를 쉽게 유지하려면 AbstractGraph
클래스를 abstract로 정의하는 것이 바람직합니다.
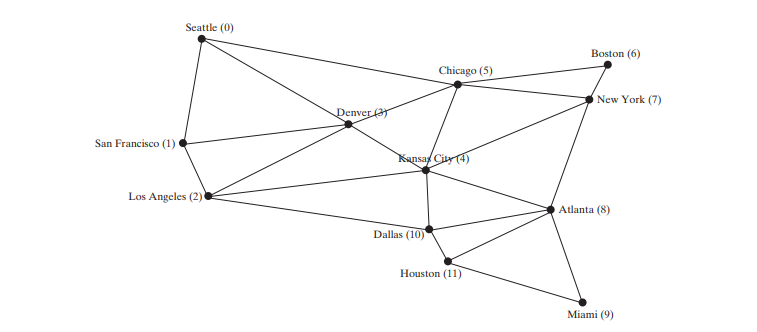
이러한 인터페이스와 클래스를 모두 사용할 수 있다고 가정합니다. 아래 코드는 위 그림의 그래프와 아래 그림(a)의 그래프에 대한 또 다른 그래프를 생성하는 테스트 프로그램을 제공합니다.
public class TestGraph {
public static void main(String[] args) {
String[] vertices = {"Seattle", "San Francisco", "Los Angeles", "Denver", "Kansas City", "Chicago", "Boston", "New York", "Atlanta", "Miami", "Dallas", "Houston"};
// Edge array for graph
int[][] edges = {
{0, 1}, {0, 3}, {0, 5},
{1, 0}, {1, 2}, {1, 3},
{2, 1}, {2, 3}, {2, 4}, {2, 10},
{3, 0}, {3, 1}, {3, 2}, {3, 4}, {3, 5},
{4, 2}, {4, 3}, {4, 5}, {4, 7}, {4, 8}, {4, 10},
{5, 0}, {5, 3}, {5, 4}, {5, 6}, {5, 7},
{6, 5}, {6, 7},
{7, 4}, {7, 5}, {7, 6}, {7, 8},
{8, 4}, {8, 7}, {8, 9}, {8, 10}, {8, 11},
{9, 8}, {9, 11},
{10, 2}, {10, 4}, {10, 8}, {10, 11},
{11, 8}, {11, 9}, {11, 10}
};
Graph<String> graph1 = new UnweightedGraph<>(vertices, edges);
System.out.println("The number of vertices in graph1: " + graph1.getSize());
System.out.println("The vertex with index 1 is " + graph1.getVertex(1));
System.out.println("The index for Miami is " + graph1.getIndex("Miami"));
System.out.println("The edges for graph1:");
graph1.printEdges();
// List of Edge objects for graph
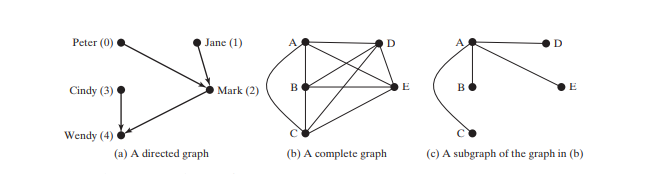
String[] names = {"Peter", "Jane", "Mark", "Cindy", "Wendy"};
java.util.ArrayList<AbstractGraph.Edge> edgeList = new java.util.ArrayList<>();
edgeList.add(new AbstractGraph.Edge(0, 2));
edgeList.add(new AbstractGraph.Edge(1, 2));
edgeList.add(new AbstractGraph.Edge(2, 4));
edgeList.add(new AbstractGraph.Edge(3, 4));
// Create a graph with 5 vertices
Graph<String> graph2 = new UnweightedGraph<>(java.util.Arrays.asList(names), edgeList);
System.out.println("\nThe number of vertices in graph2: " + graph2.getSize());
System.out.println("Te edges for graph2:");
graph2.printEdges();
}
}
graph1의 정점 수: 12
인덱스 1의 꼭지점은 샌프란시스코입니다
마이애미 지수는 9
graph1의 가장자리:
시애틀 (0): (0, 1) (0, 3) (0, 5)
샌프란시스코 (1): (1, 0) (1, 2) (1, 3)
로스앤젤레스 (2): (2, 1) (2, 3) (2, 4) (2, 10)
덴버 (3): (3, 0) (3, 1) (3, 2) (3, 4) (3, 5)
캔자스시티(4): (4, 2) (4, 3) (4, 5) (4, 7) (4, 8) (4, 10)
시카고 (5): (5, 0) (5, 3) (5, 4) (5, 6) (5, 7)
보스턴 (6): (6, 5) (6, 7)
뉴욕(7): (7, 4) (7, 5) (7, 6) (7, 8)
애틀랜타 (8): (8, 4) (8, 7) (8, 9) (8, 10) (8, 11)
마이애미 (9): (9, 8) (9, 11)
댈러스(10): (10, 2) (10, 4) (10, 8) (10, 11)
The number of vertices in graph2: 5
The edges for graph2:
Peter (0): (0, 2)
Jane (1): (1, 2)
Mark (2): (2, 4)
Cindy (3): (3, 4)
Wendy (4):
The program creates graph1 for the graph in Figure 28.1 in lines 3–23. The vertices for graph1 are defined in lines 3–5. The edges for graph1 are defined in 8–21. The edges are represented using a two-dimensional array. For each row i in the array, edges[i][0] and edges[i][1] indicate that there is an edge from vertex edges[i][0] to vertex edges[i][1]. For example, the first row, {0, 1}, represents the edge from vertex 0 (edges[0][0]) to vertex 1 (edges[0][1]). The row {0, 5} represents the edge from vertex 0 (edges[2][0]) to vertex 5 (edges[2][1]). The graph is created in line 23. Line 31 invokes the printEdges() method on graph1 to display all edges in graph1.
The program creates graph2 for the graph in Figure 28.3a in lines 34–43. The edges for graph2 are defined in lines 37–40. graph2 is created using a list of Edge objects in line 43. Line 47 invokes the printEdges() method on graph2 to display all edges in graph2.
Note that both graph1 and graph2 contain the vertices of strings. The vertices are associated with indices 0, 1, . . . , n-1. The index is the location of the vertex in vertices. For example, the index of vertex Miami is 9.
Now we turn our attention to implementing the interface and classes. The codes below give the Graph interface, the AbstractGraph class, and the UnweightedGraph class, respectively.
public interface Graph<V> {
/** Return the number of vertices in the graph */
public int getSize();
/** Return the vertices in the graph */
public java.util.List<V> getVertices();
/** Return the object for the specified vertex index */
public V getVertex(int index);
/** Return the index for the specified vertex object */
public int getIndex(V v);
/** Return the neighbors of vertex with the specified index */
public java.util.List<Integer> getNeighbors(int index);
/** Return the degree for a specified vertex */
public int getDegree(int v);
/** Print the edges */
public void printEdges();
/** Clear the graph */
public void clear();
/** Add a vertex to the graph */
public void addVertex(V vertex);
/** Add an edge to the graph */
public void addEdge(int u, int v);
/** Obtain a depth-first search tree starting from v */
public AbstractGraph<V>.Tree dfs(int v);
/** Obtain a breadth-first search tree starting from v */
public AbstractGraph<V>.Tree bfs(int v);
}
import java.util.*;
public abstract class AbstractGraph<V> implements Graph<V> {
protected List<V> vertices = new ArrayList<>(); // Store vertices
protected List<List<Edge>> neighbors = new ArrayList<>(); // Adjacency lists
/** Construct an empty graph */
protected AbstractGraph() {}
/** Construct a graph from vertices and edges stored in arrays */
protected AbstractGraph(V[] vertices, int[][] edges) {
for(int i = 0; i < vertices.length; i++)
addVertex(vertices[i]);
createAdjacencyLists(edges, vertices.length);
}
/** Construct a graph from vertices and edges stored in List */
protected AbstractGraph(List<V> vertices, List<Edge> edges) {
for(int i = 0; i < vertices.size(); i++)
addVertex(vertices.get(i));
createAdjacencyLists(edges, vertices.size());
}
/** Construct a graph for integer vertices 0, 1, 2 and edge list */
protected AbstractGraph(List<Edge> edges, int numberOfVertices) {
for(int i = 0; i < numberOfVertices; i++)
addVertex((V)(new Integer(i))); // vertices is {0, 1, ...}
createAdjacencyLists(edges, numberOfVertices);
}
/** Construct a graph from integer vertices 0, 1, and edge array */
protected AbstractGraph(int[][] edges, int numberOfVertices) {
for(int i = 0; i < numberOfVertices; i++)
addVertex((V)(new Integer(i))); // vertices is {0, 1, ...}
createAdjacencyLists(edges, numberOfVertices);
}
/** Create adjacency lists for each vertex */
private void createAdjacencyLists(int[][] edges, int numberOfVertices) {
for(int i = 0; i < edges.length; i++) {
addEdge(edges[i][0], edges[i][1]);
}
}
/** Create adjacency lists for each vertex */
private void createAdjacencyLists(List<Edge> edges, int numberOfVertices) {
for(Edge edge: edges) {
addEdge(edge.u, edge.v);
}
}
@Override /** Return the number of vertices in the graph */
public int getSize() {
return vertices.size();
}
@Override /** Return the vertices in the graph */
public List<V> getVertices() {
return vertices;
}
@Override /** Return the object for the specified vertex */
public V getVertex(int index) {
return vertices.get(index);
}
@Override /** Return the index for the specified vertex object */
public int getIndex(V v) {
return vertices.indexOf(v);
}
@Override /** Return the neighbors of the specified vertex */
public List<Integer> getNeighbors(int index) {
List<Integer> result = new ArrayList<>();
for(Edge e: neighbors.get(index))
result.add(e.v);
return result;
}
@Override /** Return the degree for a specified vertex */
public int getDegree(int v) {
return neighbors.get(v).size();
}
@Override /** Print the edges */
public void printEdges() {
for(int u = 0; u < neighbors.size(); u++) {
System.out.print(getVertex(u) + " (" + u + "): ");
for(Edge e: neighbors.get(u)) {
System.out.print("(" + getVertex(e.u) + ", " + getVertex(e.v) + ") ");
}
System.out.println();
}
}
@Override /** Clear the graph */
public void clear() {
vertices.clear();
neighbors.clear();
}
@Override /** Add a vertex to the graph */
public void addVertex(V vertex) {
if(!vertices.contains(vertex)) {
vertices.add(vertex);
neighbors.add(new ArrayList<Edge>());
}
}
/** Add an edge to the graph */
protected boolean addEdge(Edge e) {
if(e.u < 0 || e.u > getSize() - 1)
throw new IllegalArgumentException("No such index: " + e.u);
if(e.v < 0 || e.v > getSize() - 1)
throw new IllegalArgumentException("No such index: " + e.v);
if(!neighbors.get(e.u).contains(e)) {
neighbors.get(e.u).add(e);
return true;
}
else {
return false;
}
}
@Override /** Add an edge to the graph */
public void addEdge(int u, int v) {
addEdge(new Edge(u, v));
}
/** Edge inner class inside the AbstractGraph class */
public static class Edge {
public int u; // Starting vertex of the edge
public int v; // Ending vertex of the edge
/** Construct an edge for (u, v) */
public Edge(int u, int v) {
this.u = u;
this.v = v;
}
public boolean equals(Object o) {
return u == ((Edge)o).u && v == ((Edge)o).v;
}
}
@Override /** Obtain a DFS tree starting from vertex v */
public Tree dfs(int v) {
List<Integer> searchOrder = new ArrayList<>();
int[] parent = new int[vertices.size()];
for(int i = 0; i < parent.length; i++)
parent[i] = -1; // Initialize parent[i] to -1
// Mark visited vertices
boolean[] isVisited = new boolean[vertices.size()];
// Recursively search
dfs(v, parent, searchOrder, isVisited);
// Return a search tree
return new Tree(v, parent, searchOrder);
}
/** Recursive method for DFS search */
private void dfs(int u, int[] parent, List<Integer> searchOrder, boolean[] isVisited) {
// Store the visited vertex
searchOrder.add(u);
isVisited[u] = true; // Vertex v visited
for(Edge e: neighbors.get(u)) {
if(!isVisited[e.v]) {
parent[e.v] = u; // The parent of vertex e.v is u
dfs(e.v, parent, searchOrder, isVisited); // Recursive search
}
}
}
@Override /** Starting bfs search from vertex v */
public Tree bfs(int v) {
List<Integer> searchOrder = new ArrayList<>();
int[] parent = new int[vertices.size()];
for(int i = 0; i < parent.length; i++)
parent[i] = -1; // Initialize parent[i] to -1
java.util.LinkedList<Integer> queue = new java.util.LinkedList<>(); // list used as queue
boolean[] isVisited = new boolean[vertices.size()];
queue.offer(v); // Enqueue v
isVisited[v] = true; // Mark it visited
while(!queue.isEmpty()) {
int u = queue.poll(); // Dequeue to u
searchOrder.add(u); // u searched
for(Edge e: neighbors.get(u)) {
if(!isVisited[e.v]) {
queue.offer(e.v); // Enqueue w
parent[e.v] = u; // The parent of w is u
isVisited[e.v] = true; // Mark it visited
}
}
}
return new Tree(v, parent, searchOrder);
}
/** Tree inner class inside the AbstractGraph class */
public class Tree {
private int root; // The root of the tree
private int[] parent; // Store the parent of each vertex
private List<Integer> searchOrder; // Store the search order
/** Construct a tree with root, parent, and searchOrder */
public Tree(int root, int[] parent, List<Integer> searchOrder) {
this.root = root;
this.parent = parent;
this.searchOrder = searchOrder;
}
/** Return the root of the tree */
public int getRoot() {
return root;
}
/** Return the parent of vertex v */
public int getParent(int v) {
return parent[v];
}
/** Return an array representing search order */
public List<Integer> getSearchOrder() {
return searchOrder;
}
/** Return number of vertices found */
public int getNumberOfVerticesFound() {
return searchOrder.size();
}
/** Return the path of vertices from a vertex to the root */
public List<V> getPath(int index) {
ArrayList<V> path = new ArrayList<>();
do {
path.add(vertices.get(index));
index = parent[index];
}
while(index != -1);
return path;
}
/** Print a path from the root vertex v */
public void printPath(int index) {
List<V> path = getPath(index);
System.out.print("A path from " + vertices.get(root) + " to " + vertices.get(index) + ": ");
for(int i = path.size() - 1; i >= 0; i--)
System.out.print(path.get(i) + " ");
}
/** Print the whole tree */
public void printTree() {
System.out.println("Root is: " + vertices.get(root));
System.out.print("Edges: ");
for(int i = 0; i < parent.length; i++) {
if(parent[i] != -1) {
// Display an edge
System.out.print("(" + vertices.get(parent[i]) + "' " + vertices.get(i) + ") ");
}
}
System.out.println();
}
}
}
import java.util.*;
public class UnweightedGraph<V> extends AbstractGraph<V> {
/** Construct an empty graph */
public UnweightedGraph() {}
/** Construct a graph from vertices and edges stored in arrays */
public UnweightedGraph(V[] vertices, int[][] edges) {
super(vertices, edges);
}
/** Construct a graph from vertices and edges stored in List */
public UnweightedGraph(List<V> vertices, List<Edge> edges) {
super(vertices, edges);
}
/** Construct a graph for integer vertices 0, 1, 2, and edge list */
public UnweightedGraph(List<Edge> edges, int numberOfVertices) {
super(edges, numberOfVertices);
}
/** Construct a graph from integer vertices 0, 1, and edge array */
public UnweightedGraph(int[][] edges, int numberOfVertices) {
super(edges, numberOfVertices);
}
}
The code in the Graph interface and the UnweightedGraph class are straightforward. Let us digest the code in the AbstractGraph class.
The AbstractGraph class defines the data field vertices (line 4) to store vertices and neighbors (line 5) to store edges in adjacency lists. neighbors.get(i) stores all edges adjacent to vertex i. Four overloaded constructors are defined in lines 9–42 to create a default graph, or a graph from arrays or lists of edges and vertices. The createAdjacencyLists(int[][] edges, int numberOfVertices) method creates adjacency lists from edges in an array (lines 45–50). The createAdjacencyLists(List edges, int numberOfVertices) method creates adjacency lists from edges in a list (lines 53–58).
The getNeighbors(u) method (lines 81–87) returns a list of vertices adjacent to vertex u. The clear() method (lines 106–110) removes all vertices and edges from the graph. The addVertex(u) method (lines 112–122) adds a new vertex to vertices and returns true. It returns false if the vertex is already in the graph (line 120).
The addEdge(e) method (lines 124–139) adds a new edge the adjacency edge list and returns true. It returns false if the edge is already in the graph. This method may throw IllegalArgumentException if the edge is invalid (lines 126–130).
The printEdges() method (lines 95–104) displays all vertices and edges adjacent to each vertex.
The code in lines 164–293 gives the methods for finding a depth-first search tree and a breadth-first search tree, which will be introduced in Depth-First Search (DFS) and Breadth-First Search (BFS), respectively.
위 내용은 그래프 모델링의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!